
Parser nennt man ein Programm, das einen Quelltext an Hand der Syntaxregeln einer Grammatik, die in geeigneter Weise implementiert sein müssen, auf syntaktische Richtigkeit untersucht. Der Quelltext wird dabei morphemweise verarbeitet, für die Bildung der Morpheme (oft auch als Token oder Atome bezeichnet) ist ein Lexer (oder auch Scanner) zuständig.
Die Regeln der zu Grunde liegenden Grammatik können in Tabellenform (tabellengesteuerte Verfahren), in Form von Graphen (graphengesteuerte Verfahren) oder in algorithmischer Form (Verfahren des rekursiven Abstiegs) vorliegen.
Nachfolgend wird ein graphengesteuertes Verfahren vorgestellt. Es handelt sich um ein Top-Down verfahren, das geeignet ist, linkslineare Grammatiken zu implementieren. Es bildet die Grundlage für einen sytaxgesteuerten Einpasscompiler für PL/0. Er wird bestehen aus den Programmkomponenten:
lexer
parser
Semantikroutinen / Codegenerierung
Fehlerbehandlung
Der fertige Compiler soll Code für eine virtuelle Maschine erzeugen. Diese wird als C- Quelltext bereitgestellt, so dass eine Portierung auf beliebige Plattformen problemlos möglich sein sollte.
programm= |
block “.“. |
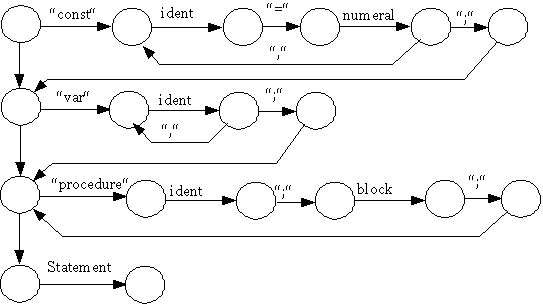
block= |
[“CONST“ ident=num{“,“ ident=num}“;“]
|
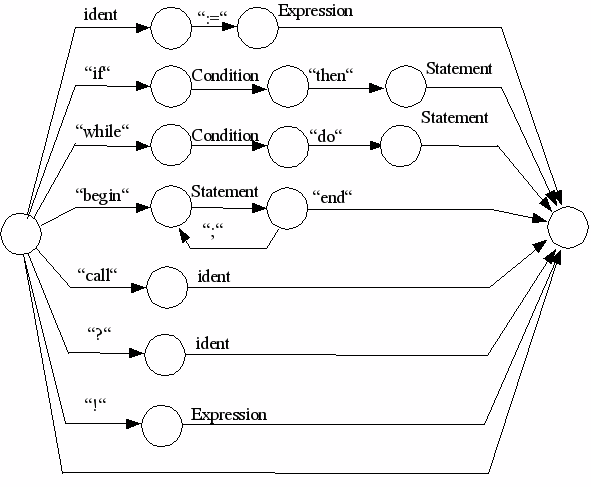
Statement= |
[ident ":=" expression | |
Condition= |
"ODD" expression | |
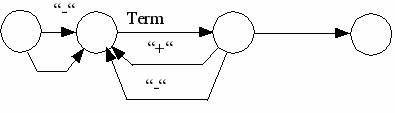
expression= |
["+" | "-"] term {("+" | "-") term }.
|
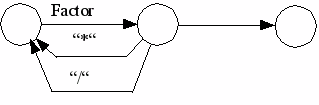
term= |
faktor { ("*"|"/") faktor }.
|
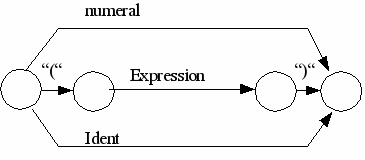
factor= |
ident | number | "(" expression ")".
|

Variante
1
Variante 1
Variante
2:

Variante 3

Variante 1
Variante 2

Variante 3
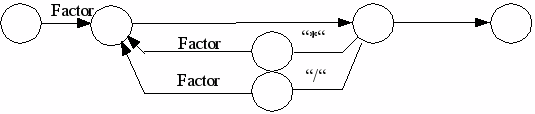
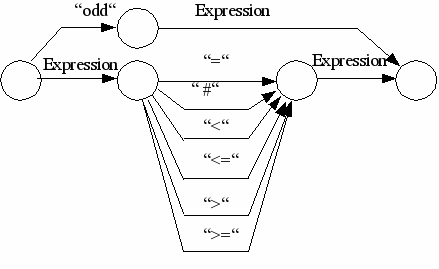
Condition:
Graphen bestehen aus Knoten und Kanten. Die Kanten hier sind mit terminalen und nicht terminalen Symbolen bewertet. Die Bewertungen der Bögen lassen sich klassifizieren, die sich ergebenden Bogentypen sind nachfolgend erläutert und hervorgehoben, sie spielen bei der Umsetzung in die interne Repräsentation eine Rolle.
Nicht Terminales Symbol oder Graph, der Bogen ist mit einem Metasymbol bewertet (Programm, Block, Statement, Expression, Term, Factor, Condition). In der Bogenbeschreibung wird die Adresse eines Graphen angegeben.
Symbol, der Bogen ist mir einem einfachen Sonderzeichen, hier eingeschlossen in ““bewertet. PL/0 verwendet folgende einfache Sonderzeichen: +, -, *, /, (, ), ?, !, ;, =, #, <, >, . . Weiterhin gibt es zusammengesetzte Symbole (:=, <=, >=). Aber auch die Wortsymbole (Schlüsselwörter) werden zu den Symbolen gezählt (begin, const, call, do, end, if, odd, procedure,then, var, while) In der internen Bogenbeschreibung wird das Sonderzeichen oder der Wortsymbolcode angegeben.
Variables Morphem, hierzu zählen numeral und ident. In der Bogenbeschreibung wird der Tokentyp (Morphemtyp) angegeben (ident oder numeral)
Ein nicht bewerteter Bogen ist ein Nil-Bogen (Nl).
#define OK 1
#define FAIL 0
typedef enum BOGEN_DESC{BgNl= 0, /* NIL */
BgSy= 1, /* Symbol */
BgMo= 2, /* Morphem */
BgGr= 4, /* Graph */
BgEn= 8, /* Graphende */
BgAl=16} /* Alternative */
tBg;
/* Ein Graph wird durch einen Vektor von Boegen beschrieben,
Jeder Bogen enthaelt den Index des Folgebogens und ggf.
den Index eines Alternativbogens */
/* Beschreibung eines Bogens eines Syntaxgraphen */
typedef struct BOGEN
{
tBg BgD; /* Kurzbeschreibung des Bogens */
union BGX /* Detaillierte Beschreibung */
{
unsigned long X; /* fuer Initialisierung */
int S; /* Symbol */
tMC M; /* Morphemcode */
struct BOGEN* G; /* Graph */
} BgX;
int (*fx)(void); /* Action/NULL */
int iNext; /* Index Folgebogen / 0 */
int iAlt; /* Index Alternativbogen / 0 */
}tBog;
Zur Umsetzung eines Graphen in die interne Struktur wird nun ein Vektor solcher Bogenbeschreibungen der Struktur tBog angelegt. Jede Bogenbeschreibung ist von einem Bogentyp, trägt eine Bogenbewertung, die für die Akzeptanz des Bogens maßgeblich ist, hat einen Folgebogen, bei dem die Analyse fortgesetzt wird, wenn der aktuelle Bogen akzeptiert worden ist und hat ggf. einen Alternativbogen, wenn der aktuelle Bogen abgelehnt wurde. Weiterhin enthält jede Bogenbeschreibung einen Funktionspointer. Hier kann die Adresse einer Funktion eingetragen werden, die ausgeführt wird, wenn der Bogen akzeptiert worden ist. In der hier aufgerufenen Funktion können nun Semantikprüfungen und (Zwischen-)Codegenerierung erfolgen. Über den Returnwert der Funktion kann der Bogen nachträglich abgelehnt werden. Die Funktionspointer werden zunächst mit einem NULL-Pointer belegt und später ergänzt.
Beispielhafte Umsetzung des Graphen Expression Variante 3:
Schritt 1: Nummerierung der Bögen (Kanten)
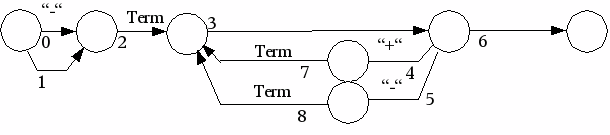
Der NIL-Bogen Nummer 3 kann entfallen
Schritt 2: Nummerierung der Knoten (Nur für Kommentare/Dokumentation)
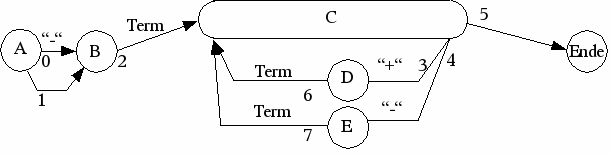
Schritt 3 bogenweise Übertragung in die Struktur
Bogen 0:
wird als erster Bogen per Initialisierung angelegt. Bogentyp ist Symbol (“-“).
Folgebogen ist der Bogen 2,
Alternativbogen ist Bogen 1 ( oder 2, der Nil-Bogen könnte entfallen, wenn als Folge- und Alternativbogen Bogen 2 angegeben wird)
tBog gExpr[]=
{
/*index Typ Bogenbewertung Action FB AB Quellknoten Zielknoten */
/* 0*/ {BgSy,{(unsigned long)'-' }, NULL, 2, 1},/* A------'-'--->(B) */
Bogen 1:
Zweiter Bogen des Arrays von Bogenbeschreibungen
Bogentyp ist nil
Bogen könnte auch entfallen, wenn in Bogen 0 für Folgebogen und Alternativbogen Bogen 2 eingetragen wird.
NIL-Bögen müssen immer als letzte Alternative auftreten, da sie immer akzeptiert werden. Ebenso sollten Bögen, die mit einem Metasymbol bewertet sind (Typ Gr), immer als letzte Alternative angeführt werden, da sonst ein „backtracking“ Mechanismus nötig wird, der in vielen Fällen entfallen kann.
tBog gExpr[]=
{
/*index Typ Bogenbewertung Action FB AB Quellknoten Zielknoten */
/* 0*/ {BgSy,{(unsigned long)'-' }, NULL, 2, 1},/* A------'-'--->(B) */
/* 1*/ {BgNl,{(unsigned long)0 }, NULL, 2, 0},/* +------------>(B) */
Bogen 2:
Dritter Bogen des Arrays.
Ist bewertet mit einem Metasymbol, in der Bogenbewertung steht die Adresse eines weiteren Graphen.
Es gibt keine Alternative, wenn dieser Bogen nicht erfolgreich durchlaufen wurde, liegt ein Syntaxfehler vor.
tBog gExpr[]=
{
/*index Typ Bogenbewertung Action FB AB Quellknoten Zielknoten */
/* 0*/ {BgSy,{(unsigned long)'-' }, NULL, 2, 1},/* A------'-'--->(B) */
/* 1*/ {BgNl,{(unsigned long)0 }, NULL, 2, 0},/* +------------>(B) */
/* 2*/ {BgGr,{(unsigned long)gTerm }, NULL, 3, 0},/*(B)----term--->(C) */
Bogen 3:
Bogen mit dem Operator +.
Ist vom Typ BgSy und mit dem Zeichen “+“ bewertet.
Der Folgebogen ist der 2. Operand term.
Der Alternativbogen ist Bogen 4, der Minusoperand
tBog gExpr[]=
{
/*index Typ Bogenbewertung Action FB AB Quellknoten Zielknoten */
/* 0*/ {BgSy,{(unsigned long)'-' }, NULL, 2, 1},/* A------'-'--->(B) */
/* 1*/ {BgNl,{(unsigned long)0 }, NULL, 2, 0},/* +------------>(B) */
/* 2*/ {BgGr,{(unsigned long)gTerm }, NULL, 3, 0},/*(B)----term--->(C) */
/* 3*/ {BgSy,{(unsigned long)'+' }, NULL, 6, 4},/*(C)-----'+'--->(D) */
u.s.w.
Das Ergebnis ist eine interne Syntaxdarstellung, die gut les- und nachvollziebar ist. Syntaxbeschreibung und Routinen zur semantischen Analyse oder Codegenerierung sind klar voneinenander getrennt.
tBog gExpr[]=
{
/*index Typ Bogenbewertung Action FB AB Quellknoten Zielknoten */
/* 0*/ {BgSy,{(unsigned long)'-' }, NULL, 2, 1},/* A------'-'--->(B) */
/* 1*/ {BgNl,{(unsigned long)0 }, NULL, 2, 0},/* +------------>(B) */
/* 2*/ {BgGr,{(unsigned long)gTerm }, NULL, 3, 0},/*(B)----term--->(C) */
/* 3*/ {BgSy,{(unsigned long)'+' }, NULL, 6, 4},/*(C)-----'+'--->(D) */
/* 4*/ {BgSy,{(unsigned long)'-' }, NULL, 7, 5},/* +------'-'--->(E) */
/* 5*/ {BgEn,{(unsigned long)0 }, NULL, 0, 0},/* +------------>(Ende) */
/* 6*/ {BgGr,{(unsigned long)gTerm }, NULL, 3, 0},/*(D)----term--->(C) */
/* 7*/ {BgGr,{(unsigned long)gTerm }, NULL, 3, 0} /*(E)----term--->(C) */
};
Die Funktionspointer für die Aktionen werden zunächst auf NULL gesetzt und später eingetragen.
Algorithmus, der über den Bögen agiert, die Funktion
parse()
Die Funktion parse ist das Kernstück des Parsers. Sie wird aufgerufen mit einem Graphen als Parameter. Der Start des Parsers erfolgt mit dem Aufruf pars(gProg);. Immer wenn ein Bogen mit einem Metasymbol (BgGr) bewertet ist, erfolgt ein rekursiver Aufruf dieser Funktion pars mit jeweils dem angegebenen Graphen als Parameter. Der Aufrufstack von C ist hier etwas versteckt gewissermaßen der Analysekeller des Kellerautomaten. Der zu parsende Quelltext wird morphemweise vom Lexer gelesen. Jeder Aufruf von lex liefert jeweils ein Morphem.
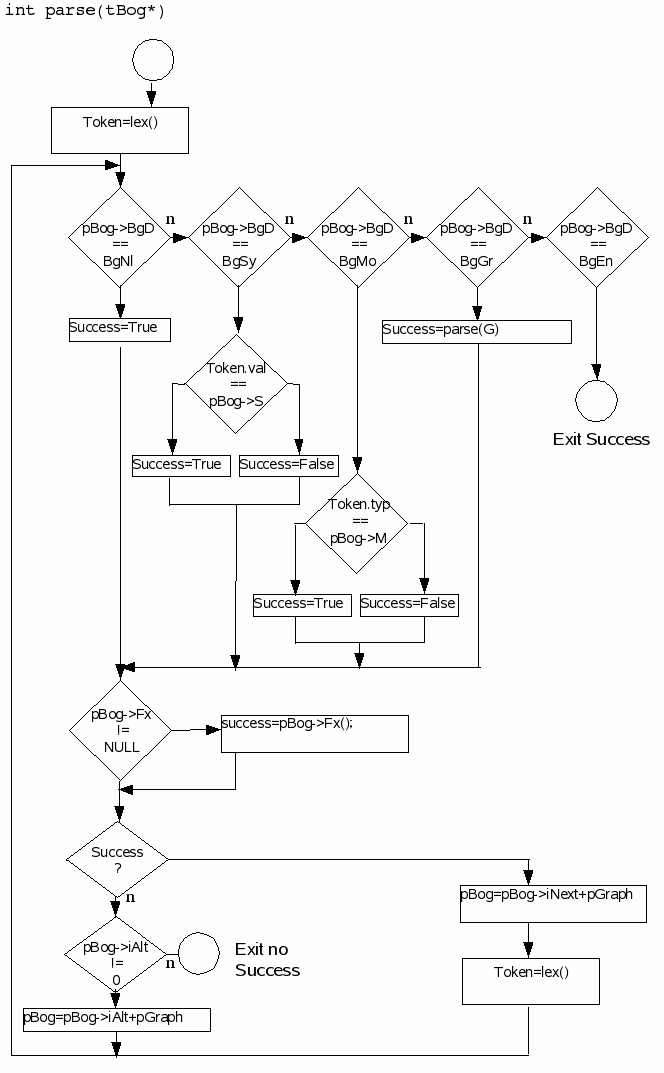
Die Funktion pars als c-Quelltext
int pars(tBog* pGraph)
{
tBog* pBog=pGraph;
int succ;
if (Morph.MC==mcEmpty)Lex();
while(1)
{
switch(pBog->BgD)
{
case BgNl:succ=1; break;
case BgSy:succ=(Morph.Val.Symb==pBog->BgX.S);break;
case BgMo:succ=(Morph.MC==(tMC)pBog->BgX.M); break;
case BgGr:succ=pars(pBog->BgX.G); break;
case BgEn:return 1; /* Ende erreichet - Erfolg */
}
if (succ && pBog->fx!=NULL) succ=pBog->fx();
if (!succ)
/* Alternativbogen probieren */
{
if (pBog->iAlt != 0)
{
pBog=pGraph+pBog->iAlt;
}
else return 0;
}
else /* Morphem formal akzeptiert */
{
if (pBog->BgD & BgSy || pBog->BgD & BgMo)
{
Lex();
}
pBog=pGraph+pBog->iNext;
}
}/* while */
}
Es ergibt sich somit folgende main-Funktion für den PL/0 parser:
main(int argc, void*argv[])
{
if (argc>1) /* PL/0-Datei angegeben ? */
if (initLex(argv[1])) /* Open in lexer o.k.? */
{
if (pars(gProg)==1) /* Start des Parsers */
{
printf ("\n OK\n");
}
else Error(ESyntx); /* Ausgabe eines Syntaxfehlers */
}
else printf("Dateifehler\n");
return 0;
}
Ein Parser nach dem hier vorgestellten Verfahren besteht somit aus: