Einführung in Lage- und Streuungsmaße der Statistik#
Einleitung: Wozu dient die deskriptive Statistik?#
Die deskriptive Statistik dient dazu, Datenmengen zusammenzufassen, zu organisieren und darzustellen. Dabei werden zentrale Tendenzen, Streuungsmaße und Verteilungen untersucht, um die wesentlichen Eigenschaften einer Datenmenge zu beschreiben.
Ziele der deskriptiven Statistik:#
Datenübersicht schaffen: Sie hilft, große und komplexe Datensätze durch geeignete Kennzahlen und Visualisierungen verständlich zu machen.
Entdeckung von Mustern: Durch die Analyse von Mittelwerten, Streuungen und Verteilungen können grundlegende Muster und Trends identifiziert werden.
Vergleiche ermöglichen: Unterschiedliche Datensätze können anhand von Kennzahlen wie Mittelwert, Median oder Standardabweichung direkt verglichen werden.
Basis für weitere Analysen schaffen: Sie bildet die Grundlage für die inferentielle Statistik, die Aussagen über Grundgesamtheiten trifft.
Beispielsweise könnten in einer Studie die Körpergrößen von Personen untersucht werden. Die deskriptive Statistik würde die durchschnittliche Größe (Mittelwert), die typische Größe (Median) und die Streuung der Größen (z. B. Standardabweichung) beschreiben.
In den folgenden Abschnitten werden wir uns die wichtigsten Kennzahlen und Konzepte der deskriptiven Statistik ansehen und anhand praktischer Beispiele veranschaulichen.
Lage: Mittelwert (Arithmetisches Mittel)#
Der Mittelwert ist ein Maß für die zentrale Tendenz einer Datenmenge. Er wird berechnet, indem man die Summe aller Beobachtungen durch deren Anzahl teilt:
[ \text{Mittelwert} = \frac{\sum_{i=1}^{n} x_i}{n} ]
Beispiel:#
Angenommen, wir haben die Daten: ([4, 8, 6, 5, 3]). Der Mittelwert wird wie folgt berechnet:
# Daten
daten <- c(4, 8, 6, 5, 3)
# Mittelwert berechnen
mittelwert <- mean(daten)
mittelwert
Lage: Median#
Der Median ist der Wert, der die Daten in zwei Hälften teilt, wenn sie der Größe nach sortiert sind. Wenn die Anzahl der Daten gerade ist, ist der Median der Durchschnitt der beiden mittleren Werte.
Beispiel:#
Die Daten ([4, 8, 6, 5, 3]) sortiert ergeben ([3, 4, 5, 6, 8]). Der Median ist:
# Median berechnen
median_wert <- median(daten)
median_wert
Streuung: Varianz und Standardabweichung#
Varianz#
Die Varianz misst die durchschnittliche quadratische Abweichung der Daten vom Mittelwert:
[ \text{Varianz} = \frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n} ]
Standardabweichung#
Die Standardabweichung ist die Wurzel aus der Varianz und wird oft verwendet, da sie die gleiche Einheit wie die Daten hat:
[ \text{Standardabweichung} = \sqrt{\text{Varianz}} ]
Beispiel:#
Die Varianz und Standardabweichung der Daten ([4, 8, 6, 5, 3]) werden wie folgt berechnet:
# Varianz berechnen
varianz <- var(daten)
varianz
# Standardabweichung berechnen
standardabweichung <- sd(daten)
standardabweichung
Visualisierung: Boxplot#
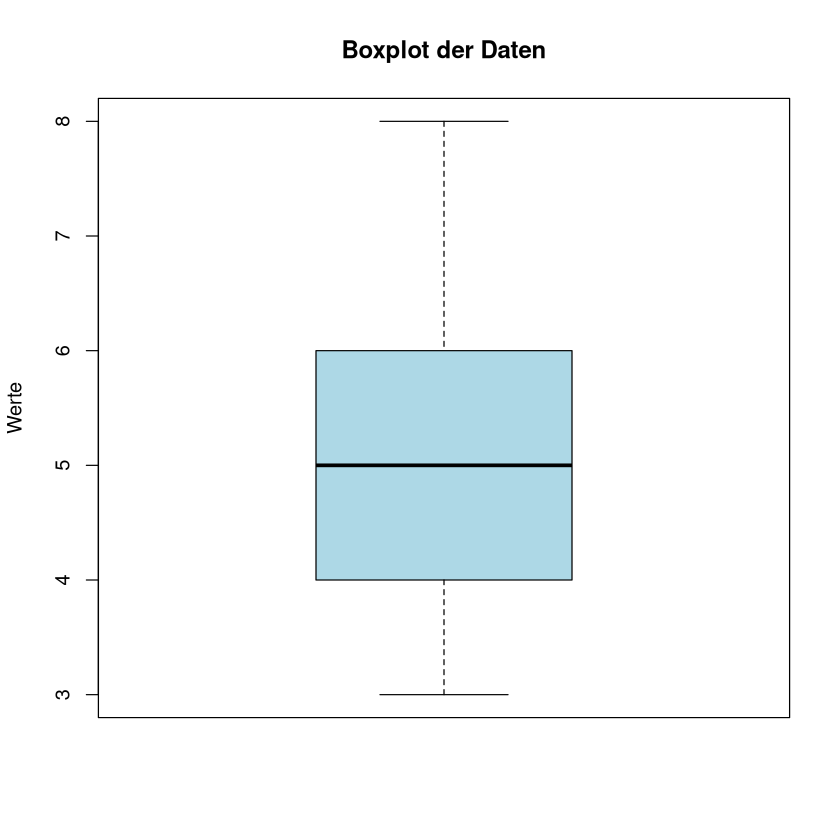
Ein Boxplot ist ein hilfreiches Werkzeug zur Visualisierung von Lage- und Streuungsmaßen. Er zeigt den Median, Quartile, und mögliche Ausreißer der Daten.
Beispiel:#
Wir erstellen einen Boxplot für die Daten ([4, 8, 6, 5, 3]):
# Boxplot erstellen
boxplot(daten, main = "Boxplot der Daten", ylab = "Werte", col = "lightblue")
