Weitere Diagramme#
Säulen- und Balkendiagramme#
Was sind Säulen- und Balkendiagramme?#
Säulen- und Balkendiagramme sind grafische Darstellungsformen von Daten, bei denen rechteckige Balken oder Säulen verwendet werden, um die Werte verschiedener Kategorien zu zeigen.
Säulendiagramme haben vertikale Balken. Balkendiagramme haben horizontale Balken. Jede Säule oder jeder Balken repräsentiert eine Kategorie, und die Länge bzw. Höhe gibt den zugehörigen Wert an. Diese Diagramme eignen sich besonders gut für Vergleiche zwischen verschiedenen Gruppen oder Kategorien.
Sie helfen dabei:
Daten übersichtlich darzustellen
Vergleiche zwischen Kategorien einfach zu erkennen
Trends und Muster sichtbar zu machen
Unterschiede schnell erfassbar zu machen
Einfache Säulen- und Balkendiagramme#
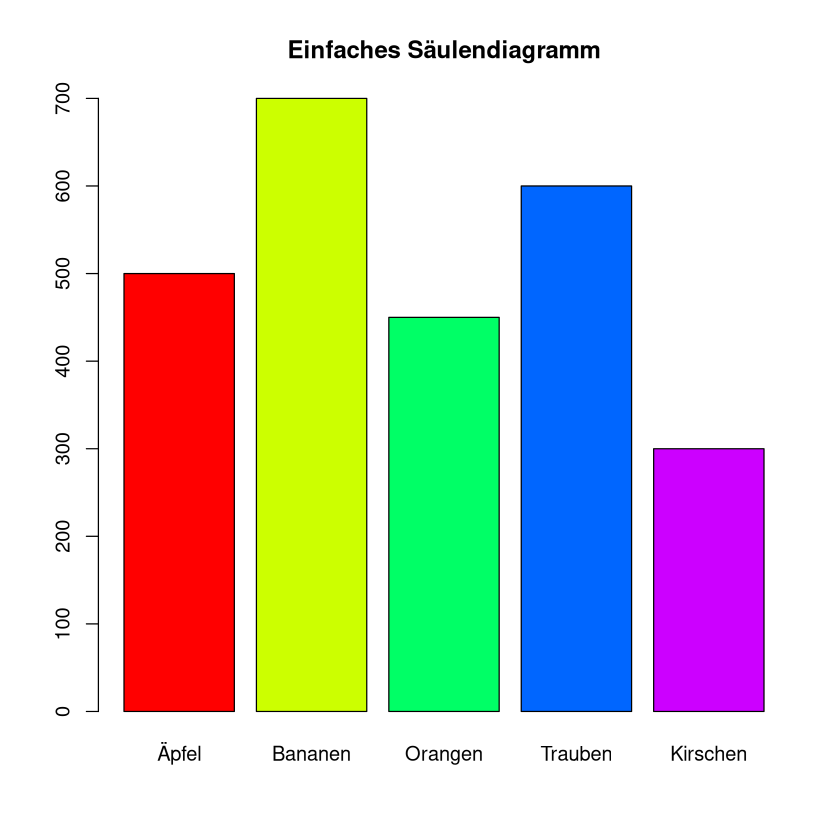
Ein Unternehmen möchte den Umsatz verschiedener Produkte vergleichen. Ein Säulendiagramm zeigt den Umsatz jedes Produkts in einer eigenen Säule, sodass sofort ersichtlich ist, welches Produkt am erfolgreichsten ist.
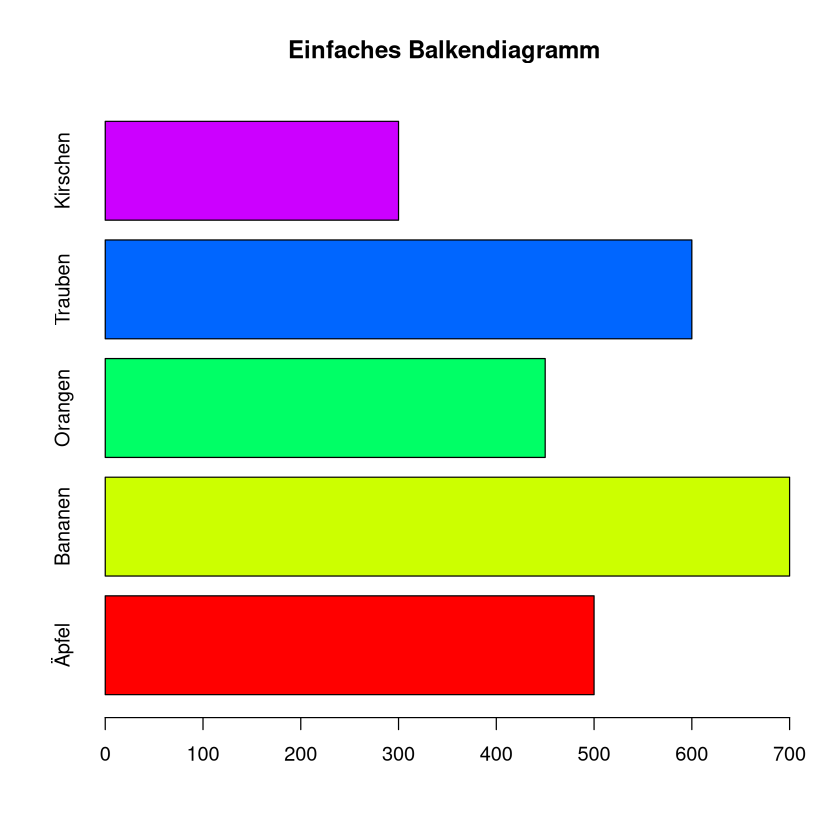
Beispiel: Ein Obsthändler will darstellen wieviele kg er von den verschiedenen Obstsorten verkauft hat
Äpfel |
Bananen |
Orangen |
Trauben |
Krischen |
|---|---|---|---|---|
500 |
700 |
450 |
600 |
300 |
Show code cell source
data1 <- data.frame(Obst = c("Äpfel", "Bananen", "Orangen", "Trauben", "Kirschen"),
Verkaufszahlen = c(500, 700, 450, 600, 300))
barplot(data1$Verkaufszahlen, names.arg = data1$Obst, col = rainbow(5), main = "Einfaches Säulendiagramm")
barplot(data1$Verkaufszahlen, names.arg = data1$Obst,horiz = TRUE, col = rainbow(5), main = "Einfaches Balkendiagramm")
Gruppiertes Balkendiagramm#
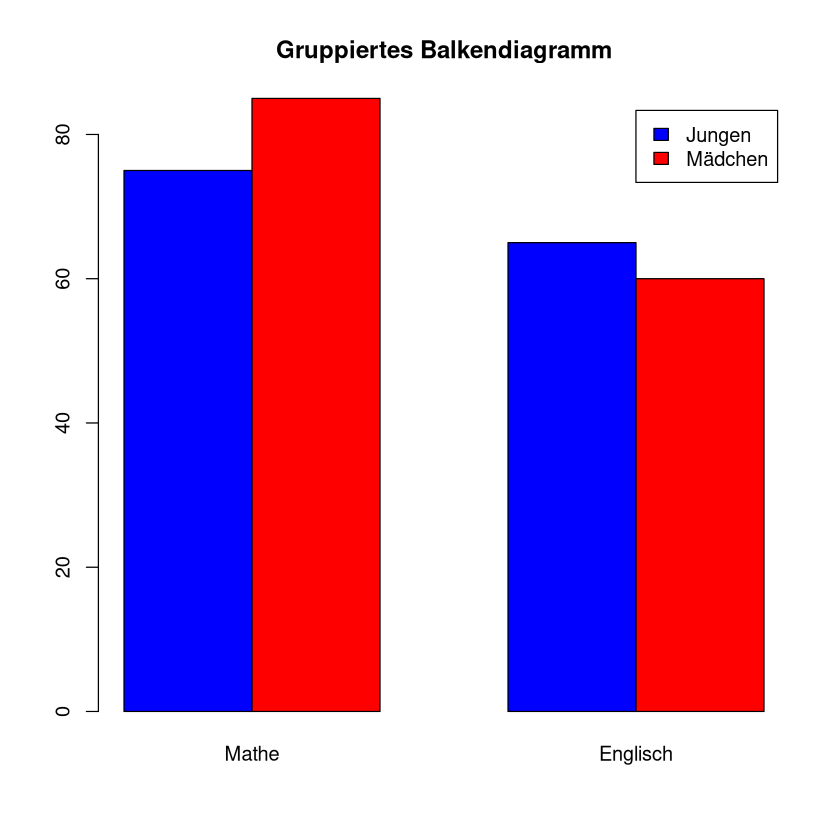
Liegen Messungen für Gruppen und Untergruppen vor, so bietet sich ein gruppiertes Säulendiagramm an.
Beispiel: Die Durchschnittspunkte der Jungen und Mädchen in der letzten Mathearbeit und Englischarbeit (von je 100) sind
Mathe |
Englisch |
|
|---|---|---|
Jungen |
75 |
65 |
Mädchen |
85 |
60 |
Wir nutzen wieder den Befehl barplot() um dies in R umzusetzen. Das erste Argument, sagt welche daten wir darstellen wollen. Sie heißen hier data2 und sind eine Matrix. Die Anweisung beside=TRUE, was dafür sorgt, dass die Säulen nebeneinander dargestellt werden. Was passiert, wenn wir diese weglassen (oder auf FALSE setzen, sehen wir im nächsten Kapitel. Der Eintrag col=c("blue","red") legt die Farben fest. mit legend=rownames(data2) fügt man eine Legende, in welcher die Zeilennamen der Matrix data2 stehen, hinzu. Mit main="..."fügt man einen Titel hinzu.
Show code cell source
data2 <- matrix(c(75, 65, 85, 60), nrow = 2, byrow = TRUE,
dimnames = list(c("Jungen", "Mädchen"), c("Mathe", "Englisch")))
barplot(data2, beside = TRUE, col = c("blue", "red"), legend = rownames(data2), main = "Gruppiertes Balkendiagramm")
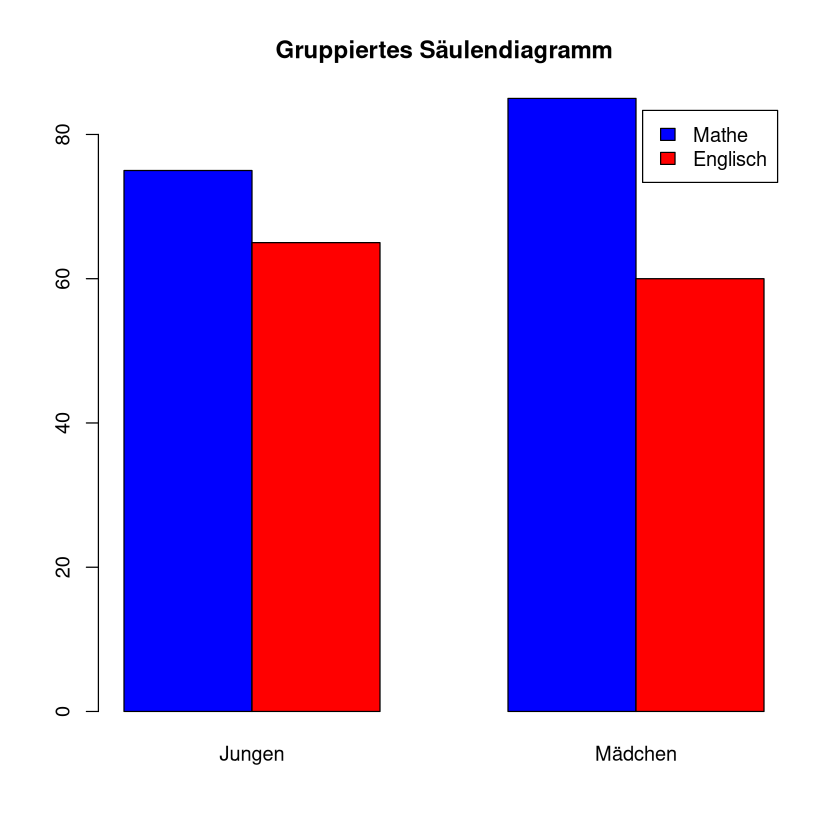
Um die Gruppen zu vertauschen, transponieren wir die Matrix mit dem Befehl t(). Außerdem muss in der Legende nun statt rownames (Zeilen-Namen) der Begriff colnames (Spalten-Namen) stehen.
Show code cell source
barplot(t(data2), beside = TRUE, col = c("blue", "red"), legend = colnames(data2), main = "Gruppiertes Säulendiagramm")
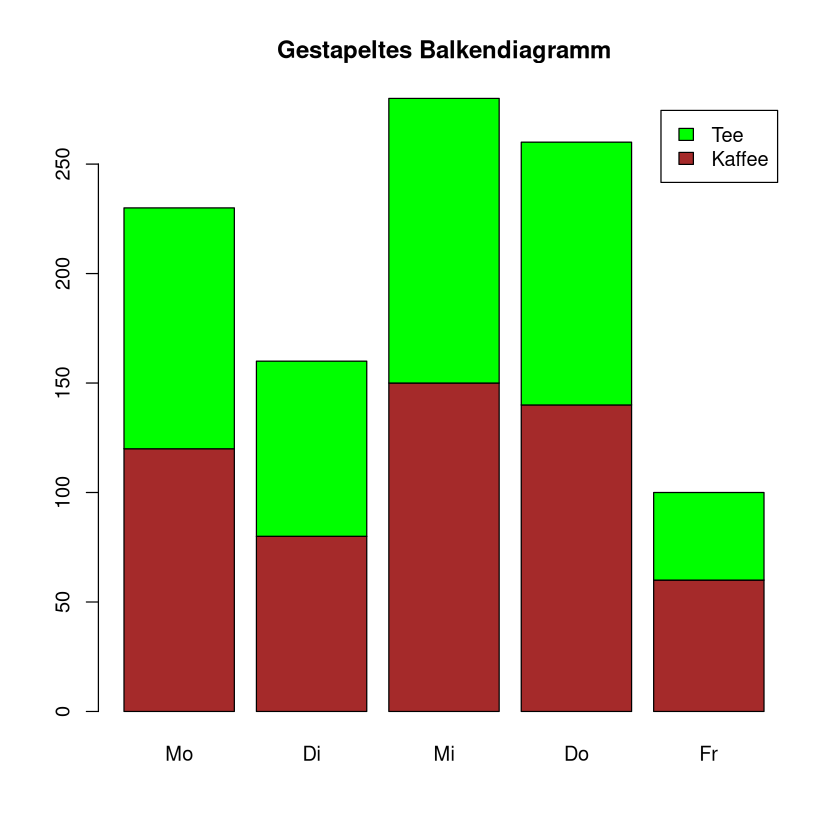
Gestapeltes Säulendiagramm#
In einem Stapeldiagramm werden die Häufigkeiten zusammengehöriger Untergruppen in einer Säule gemeinsam dargestellt. Dabei wird die Säule entsprechend der Untergruppen horizontal geteilt. Säulen der Untergruppen werde somit übereinander dargestellt, also gestapelt
Beispiel Die Cafeteria der HTW notiert über eine Woche die Anzahl der verkauften Tee und Kaffee pro Tag.
Montag |
Dienstag |
Mittwoch |
Donnerstag |
Freitag |
|
|---|---|---|---|---|---|
Kaffee |
120 |
80 |
150 |
140 |
60 |
Tee |
110 |
‚90 |
130 |
120 |
30 |
Um dies als gestapeltes Säulendiagramm darzustellen, lassen wir den Befehl beside=TRUE einfach weg (oder wir schreiben beside=FALSE).
data3 <- matrix(c(120, 80, 150, 140, 60, 110,80,130,120,40), nrow = 2, byrow = TRUE,
dimnames = list(c("Kaffee", "Tee"), c("Mo", "Di", "Mi","Do","Fr")))
barplot(data3, col = c("brown", "green"), legend = rownames(data3), main = "Gestapeltes Balkendiagramm")
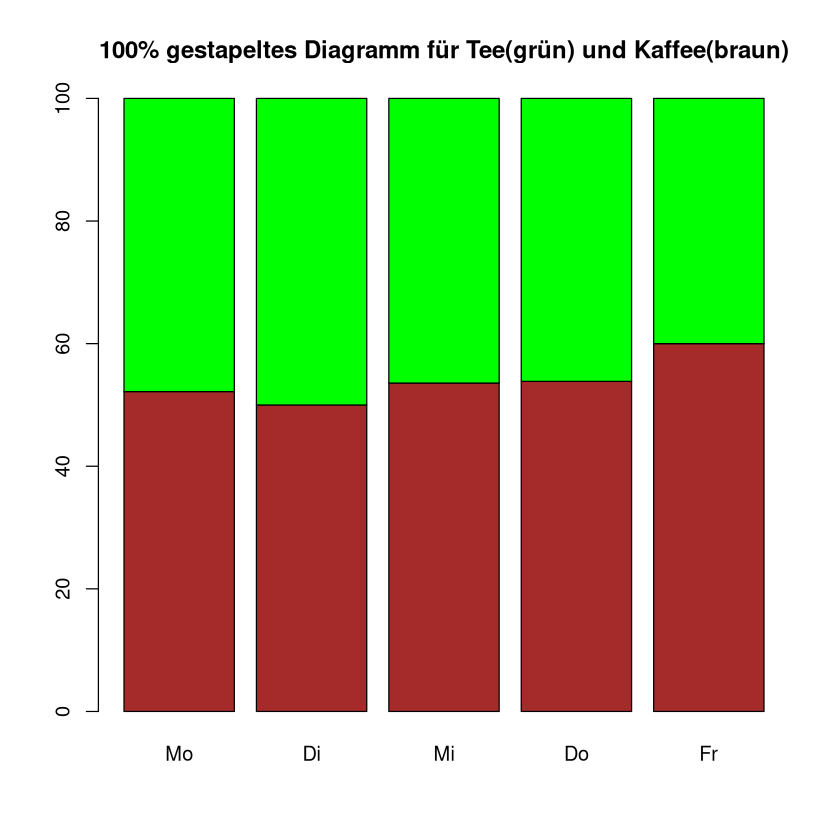
100% gestapeltes Säulendiagramm#
Interessiert uns nicht die genaue Menge, sondern nur die Proportion der Untergruppen, so kann man die gestapelten Säulen auf 100% skalieren.
Beispiel Wir nutzen die Daten aus dem vorherigen Beispiel. Nun wollen wir für jeden Wochentag anzeigen, wieviel Prozent der verkauften Getränke Kaffee waren und wieviel Tee.
Der Befehl prop.table(data3,2) überführt die absoluten Häufigkeiten in relative Häufigkeiten. Die Ausgabe ist wieder eine Matrix, die wir in den barplot-Befehl einsetzen können. Die 2 im Befehl bedeutet, dass wir jeweils die Spaltensumme als 100% betrachten wollen.
prop.table(data3,2)
barplot(prop.table(data3, 2) * 100, col = c("brown", "green"), main = "100% gestapeltes Diagramm für Tee(grün) und Kaffee(braun)")
| Mo | Di | Mi | Do | Fr | |
|---|---|---|---|---|---|
| Kaffee | 0.5217391 | 0.5 | 0.5357143 | 0.5384615 | 0.6 |
| Tee | 0.4782609 | 0.5 | 0.4642857 | 0.4615385 | 0.4 |
Wir können die Daten auch „andersum“ darstellen:
prop.table(data3,1)
barplot(t(prop.table(data3, 1)) * 100, main = "100% gestapeltes Diagramm, Mo(unten) bis Fr(oben)")
| Mo | Di | Mi | Do | Fr | |
|---|---|---|---|---|---|
| Kaffee | 0.2181818 | 0.1454545 | 0.2727273 | 0.2545455 | 0.10909091 |
| Tee | 0.2291667 | 0.1666667 | 0.2708333 | 0.2500000 | 0.08333333 |
Kreisdiagramme#
Eine weitere einfache Möglichkeit Daten darzustellen ist ein Kreisdiagramm. Sind Häufigkeiten gegeben, so stellt man diese mit Kreissektoren dar. Dabei ist der Winkel \(\varphi_i\) des Sektors direkt proportional zur relativen Häufigkeit \(f_i\) einer Ausprägung, genauer gilt für jede Ausprägung \(a_i\)
\(\varphi_i = 360^\circ \cdot f_i = 2\pi \cdot f_i\)
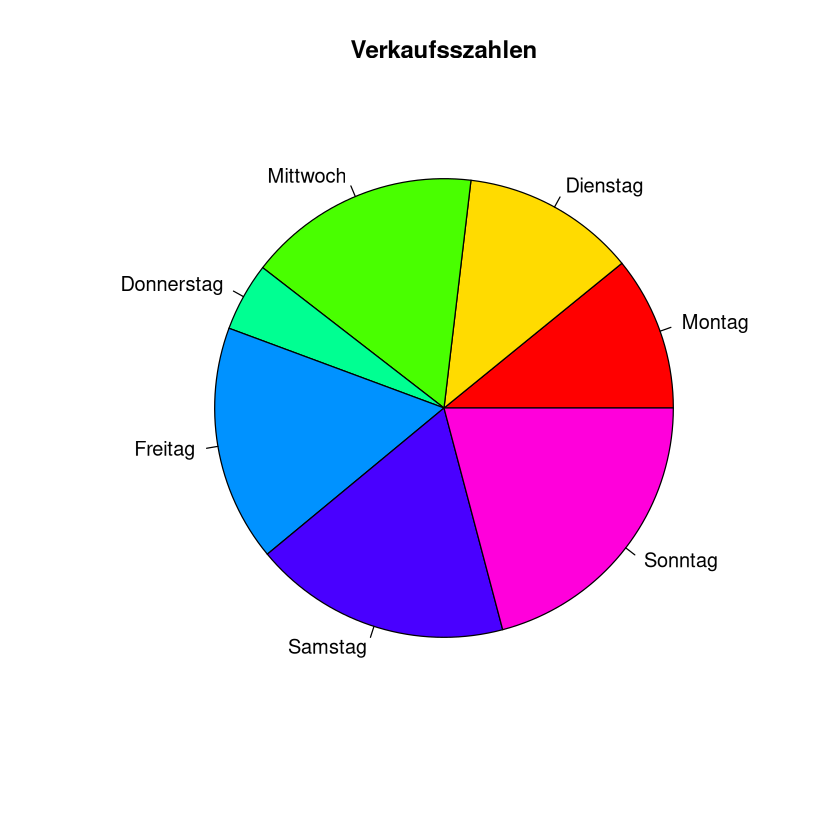
Beispiel Das Eiscafe Sonnenschein hat notiert wieviele Kugeln Eis an die verschiedenen Wochentagen verkauft wurden.
eis <- data.frame(
Tag = c("Montag", "Dienstag", "Mittwoch", "Donnerstag","Freitag","Samstag","Sonntag"),
Verkauf = c(126, 142, 190,56,193,210,242)
)
eis
pie(eis$Verkauf,
labels=eis$Tag,
col=rainbow(length(eis$Verkauf)),
main="Verkaufsszahlen")
| Tag | Verkauf |
|---|---|
| <chr> | <dbl> |
| Montag | 126 |
| Dienstag | 142 |
| Mittwoch | 190 |
| Donnerstag | 56 |
| Freitag | 193 |
| Samstag | 210 |
| Sonntag | 242 |
In R gibt es auch die Möglickeit ein 3D-Kreisdiagramm zu plotten. Dies sieht zwar auf den ersten Blick nett aus, tatsächlich lässt sich daraus schlechter das Größenverhältnis der Häufigkeiten ablesen.
library(plotrix)
pie3D(eis$Verkauf, labels=eis$Tag, explode=0.1, main="Zaubertrank-Verkäufe")
