Was ist Statistik?#
Ausgangspunkt#
Die Erhebung von Daten erfolgt durch Wissenschaftler, Unternehmen, Behörden und andere Akteure.
Statistik bietet Methoden zur Darstellung, Analyse und Auswertung von Daten im Hinblick auf spezifische Fragestellungen.
Definitionen#
Statistik ist die Gesamtheit aller Methoden zur Datenanalyse.
Statistik ist die Wissenschaft von der zahlenmäßigen Erfassung, Untersuchung und Auswertung von Massenerscheinungen. (Duden)
Umfassendes methodisch-quantitatives Instrumentarium zur Charakterisierung und Auswertung empirischer Befunde bei gleichartigen Einheiten („Massenphänomenen“) mit universellen Einsatzmöglichkeiten in Politik, Wirtschaft und Gesellschaft sowie allen Geistes-, Sozial- und Naturwissenschaften einschließlich Medizin und Technik, in denen mit Zahlen oder Bewertungen gearbeitet wird. (Gabler Wirtschaftslexikon)
Achtung Mehrdeutigkeit
Das Ergebnis von statistischen Untersuchungen wird oft ebenfalls als Statistik bezeichnet.
In der Schätztheorie werden wir Schätzer (Schätzfunktionen) kennenlernen, die ebenfalls oft als Statistik bezeichnet werden.
Typische Fragestellungen#
Die folgenden Beispiele verdeutlichen die Bandbreite an Fragen, die mithilfe von Statistik beantwortet werden können, und zeigen, dass es in allen Lebensbereichen Anwendungen gibt:
Wirtschaft und Arbeitsmarkt
Erhöht die Einführung von Mindestlöhnen die Arbeitslosigkeit in bestimmten Branchen?Gesundheit und Medizin
Ist das Medikament A wirkungsvoll, und wie hoch ist die Wahrscheinlichkeit, dass Nebenwirkungen auftreten?Bildung
Hat die Einführung von kleineren Klassengrößen in Schulen einen positiven Einfluss auf die durchschnittlichen Testergebnisse der Schüler?Umwelt und Klimaforschung
Gibt es einen statistisch signifikanten Zusammenhang zwischen CO2-Emissionen und der durchschnittlichen globalen Temperatur?Marketing und Konsumentenverhalten
Wie effektiv sind bestimmte Marketingkampagnen in der Steigerung des Produktabsatzes?Technik und Qualitätssicherung
Entspricht die Ausschussquote einer Produktionsmaschine den vom Hersteller angegebenen Werten?Sozialforschung
Gibt es regionale Unterschiede im Wahlverhalten, und welche Faktoren könnten diese Unterschiede erklären?Sport und Freizeit
Welcher Spielstil erhöht die Wahrscheinlichkeit eines Sieges im Fußball, basierend auf historischen Daten?
Ziele und Inhalte der Vorlesung#
Einordnung der Statistik
Grundlegende Begriffe der Statistik
Anwendung: Verfahren der Statistik
Anfertigung, Auswertung und Interpretation deskriptiver Statistiken (Diagramme, Tabellen, …)
Untersuchung statistischer Hypothesen (Testtheorie) mit Hilfe der induktiven Statistik
Schätzen von Parametern/Kennzahlen
Zusammenhangsanalyse
Grundlagen der Wahrscheinlichkeitsrechnung
Interpretation statistischer Ergebnisse
Umsetzung statistischer Berechnungen und Analysen mit R
Allgemeine Vorgehensweise#
Von der Fragestellung zur statistischen Antwort:
Formulierung der Fragestellung
Versuchsplanung
Datenerhebung
Dateneingabe
Datenaufbereitung und Datenvalidierung (Prüfung auf Eingabe- und Erhebungsfehler)
Statistische Analyse
Auswertung der Ergebnisse
Einteilung der Statistik#
Deskriptive Statistik (Beschreibende Statistik)
Methoden zur Strukturierung, Darstellung und Beschreibung umfangreichen oder unübersichtlichen Datenmaterials
Wichtige Instrumente: Tabellen, Kennwerte, Diagramme
Induktive Statistik (Schließende Statistik)
Methoden zur Untersuchung von Stichproben zwecks Schlussfolgerungen auf die Grundgesamtheit
Wichtige Teilgebiete: Schätztheorie und Testtheorie
Explorative Statistik
Aufsuchen von Mustern und Strukturen in zumeist sehr großen Datenbeständen zur Generierung statistischer Hypothesen
Datenanalyse, Data Mining
Wie kommt die Wahrscheinlichkeitstheorie ins Spiel?#
Der Oberbegriff Stochastik teilt sich in Wahrscheinlichkeitstheorie und Statistik auf. Diese sind eng miteinander verknüpft.
Viele statistische Verfahren beruhen auf wahrscheinlichkeitstheoretischen Modellen. Um diese Verfahren zu verstehen und richtig interpretieren zu können, braucht man Wissen über diese Modelle.
Grundlage einer statistischen Analyse ist (in den meisten Fällen) eine Stichprobe, die „zufällig“ gezogen wird – zumindest wird dies so modelliert. Zur Ableitung von Erkenntnissen sind Kenntnisse der Wahrscheinlichkeitstheorie notwendig.
Komplexere Aussagen aus statistisch erhobenen Größen erfordern häufig wahrscheinlichkeitstheoretisches Wissen.
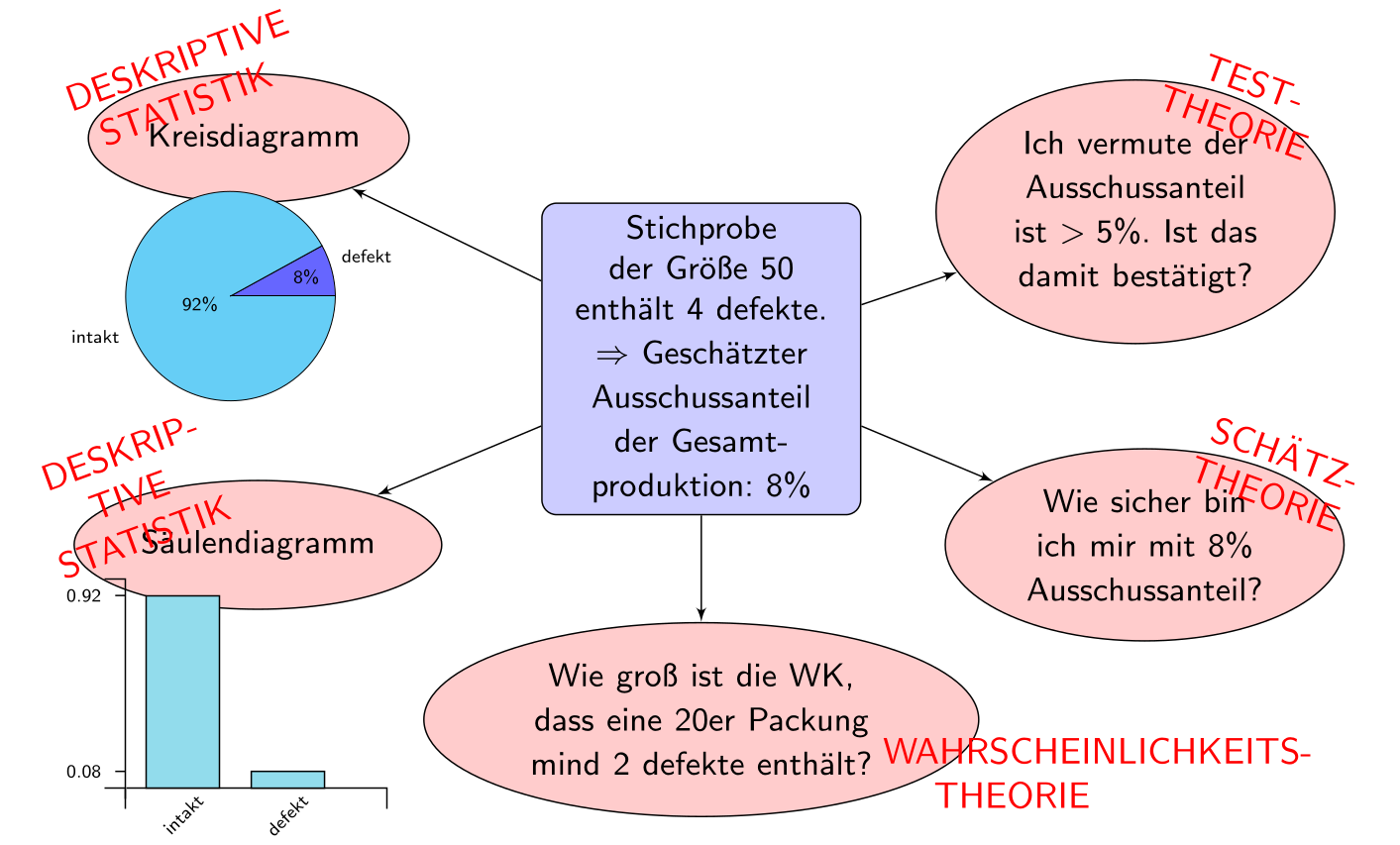
Ein Beispiel#
Der laufenden Produktion von USB-Sticks wurde eine Stichprobe der Größe 50 entnommen. Es stellt sich heraus das 4 der 50 USB-Sticks defekt waren.
