Häufigkeiten für Stichproben#
Absolute und relative Häufigkeiten#
Stichprobe: \((x_1,x_2,...,x_n)\) mit Stichprobengröße \(n\).
Ausprägungen der Stichprobe: \(a_1,..., a_k\), wobei \(a_1 < a_2 < ... < a_k\) und \(k \leq n\)
absolute Häufigkeit der Ausprägung \(a_j\), \(j=1,...,k\): Anzahl des Auftretens von \(a_j\) in der Stichprobe, d.h.
realative Häufigkeit der Ausprägung \(a_j\), \(j=1,...,k\): die absolute Häufigkeit geteilt durch \(n\), d.h.
geordnete Stichprobe \((x_{(1)},x_{(2)},...,x_{(n)})\), d.h. \(x_{(1)} \leq x_{(2)} \leq ... \leq x_{(n)}\)
Beispiel
Die letzte Klassenarbeit in Mathematik ergab die folgenden Noten:
Die Größe der Stichprobe ist \(n=30\). Die Ausprägungen \(a_j\) die hier auftreten sind:
Die absolute Häufigkeit \(h_1=h(a_1)\) ist die Häufigkeit der Ausprägung \(a_1=1\), nämlich \(h_1=6\).
Die relative Häufigkeit \(f_1=f(a_1)=\frac{h(a_1)}{n}\), also \(f_1=\frac{6}{30}=0.2\).
Die Werte für relative und absolute Häufigkeit der Ausprägungen schreiben wir in eine Tabelle und erhalten so eine gute Übersicht über die Stichprobe:
Index j |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
|---|---|---|---|---|---|---|
Ausprägung \(a_j\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
absolute Häufigkeit \(h_j\) |
\(6\) |
\(6\) |
\(9\) |
\(5\) |
\(3\) |
\(1\) |
relative Häufigkeit \(f_j\) |
\(0.2\) |
\(0.2\) |
\(0.3\) |
\(0.1\bar 6\) |
\(0.1\) |
\(0.0\bar3\) |
Bemerkung
Eine tabellarische Darstellung ist sinnvoll, solange nicht zu viele verschiedene Ausprägungen vorliegen. Beschreiben die Daten beispielsweise einzelne Zeitmessungen beim 5000-Meter-Lauf, so wird jeder Läufer seine eigene Zeit haben und daher jeder Wert nur einmal in der Stichprobe vorkommen. Hier bringt eine Zusammenfassung mit den Häufigkeiten nichts.
Der wesentliche Unterschied zwischen den beiden Beispielen ist die Art der Messbarkeit:
Noten im Unterricht (von 1 bis 6): ordinal messbar, wenige unterschiedliche Ausprägungen
Zeitmessungen beim 5000-Meter-Lauf: metrisch messbar, viele unterschiedliche Ausprägungen
Nachdem wir die Häufigkeiten tabellarisch erfasst haben, wollen wir im nächsten Abschnitt grafische Darstellungen betrachten.
Graphische Darstellung der Häufigkeiten#
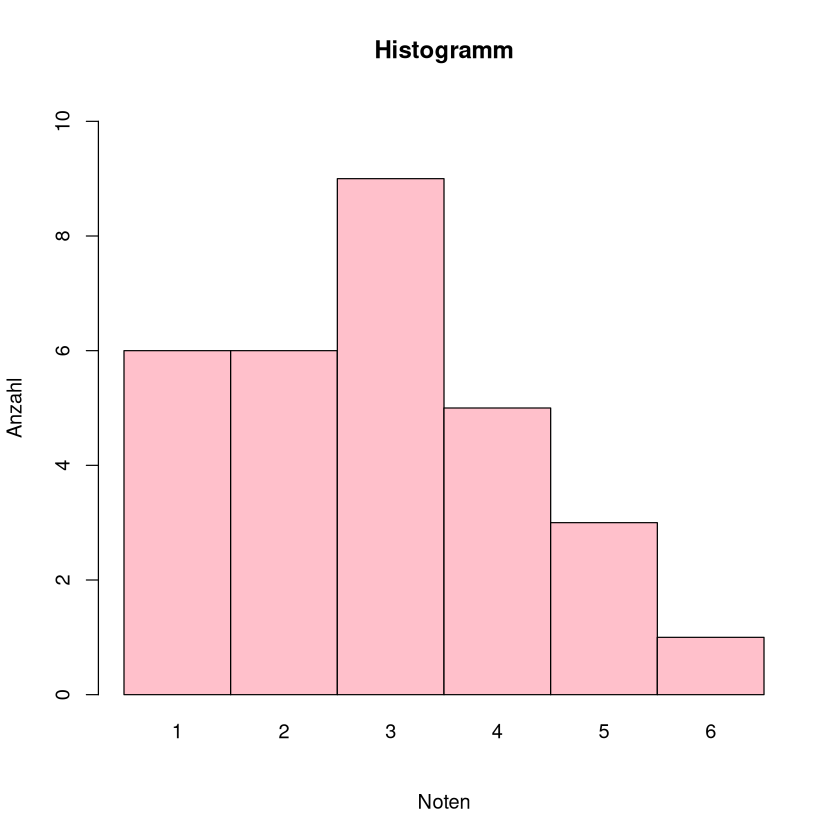
Bei wenigen Ausprägungen kann man die absoluten Häufikeiten \(h_j\), \(j=1,\dots,k\) in einem Säulendiagramm eintragen. Auf der Abszissenachse (x-Achse) wird die Ausprägung abgetragen. Auf der Ordinatenachse wird die absoltute oder relative Häufigkeit abgetragen.
Beispiel:
mit den Daten des letzten Beispiels ergibt sich
Show code cell source
# Werte einlesen
x <- c(1,5,4,1,3,5,6,3,2,3,4,5,1,2,3,2,1,4,4,3,2,2,1,3,3,2,3,4,3,1)
# Histogramm in Variable h schreiben
h <- hist(x, plot = FALSE,breaks = 0:6)
# Histogramm plotten
plot(h, xaxt = "n", xlab = "Noten", ylab = "Anzahl",
main = "Histogramm", col = "pink",ylim=c(0,10))
axis(1, h$mids, labels = c(1:6), tick = FALSE, padj= -1.5)
Klassierung von Daten#
Bei Stichproben/Messungen mit vielen verschiedenen Ausprägungen sollte man die Daten bevor man sie in einer Tabelle mit den Häufigkeiten oder in einem Histogramm darstellt, zunächst in Klassen einteilen. Dies geschieht aus Gründen der Übersichtlichkeit: Histogramme haben sonst zu viele Säulen, Tabellen haben sonst zu viele Spalten.
Beispiel: Die Körpergrößen von 100 Personen wurde (in cm) gemessen. Wir geben sie gleich als Vektor in R ein:
x<-c(169,189,176,180,179,179,181,161,179,179,161,190,181,173,189,177,164,187,174,187,
192,183,170,179,152,167,183,184,157,162,168,173,162,172,197,171,168,164,166,182,
185,174,171,179,177,189,180,167,168,172,173,179,178,164,170,178,187,168,185,179,
168,175,187,178,172,173,169,174,161,178,184,157,167,179,187,176,182,193,181,185,
174,178,175,166,168,173,162,184,169,174,163,172,194,179,181,170,172,185,186,187)
Dies ist sehr unübersichtlich. Daher teilen wir die Werte in Klassen ein, wir klassieren sie. Hier wählen wir jeweils Abstände von 10 cm und erhalten die folgende Überichtliche Tabelle mit absoluten Häufigkeiten
Show code cell source
# Häufigkeitstabelle der klassierten Daten
# table() ... erzeugt Häufigkeitstablle
# cut() ... teilt die Daten in Klassen ein
# breaks= ... wählt die Grenzen der Klassen
table(cut(x,breaks=c(150,160,170,180,190,200)))
(150,160] (160,170] (170,180] (180,190] (190,200]
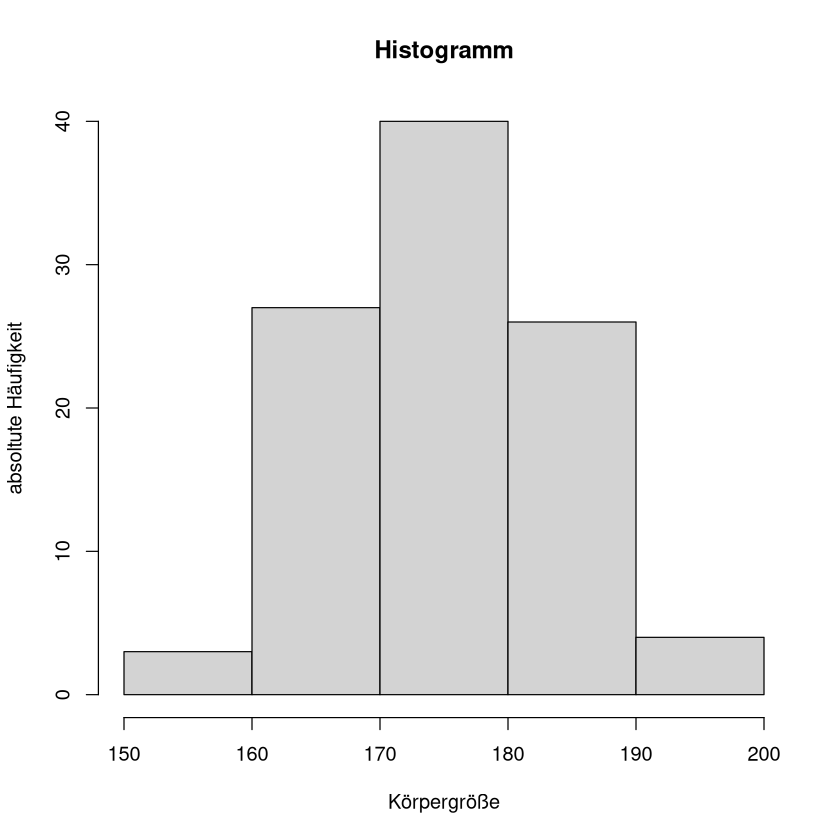
3 27 40 26 4
Das passende Histogramm ist dann dieses:
Show code cell source
hist(x,breaks = c(150,160,170,180,190,200),main = "Histogramm",xlab = "Körpergröße",ylab="absoltute Häufigkeit")
Vorgehensweise beim Klassieren#
Gegeben ist eine Stichprobe \(x_1,\dots,x_n\). Wir wählen ein \(k\leq n\) und teilen das Intervall \([x_{min},x_{max}]\) in \(k\) Intervalle ein. Dann wird jeder Wert der Stichprobe dem Intervall zugeordnet, in dem er liegt.
Wie wählt man die Anzahl \(k\) der Klassen?
Empfehlung:
\(k\approx \sqrt{n}\) falls \(n\leq 400\)
\(20\) falls \(n>400\)
Dies sind Faustregeln, keine Gesetze.
Müssen die Klassen immer gleich breit sein?
Nein, falls Sie aber alle gleich breit sind, wähle die Breite \(b\) folgendermaßen
Was gibt es zu beachten, wenn die Klassen nicht gleich breit sind?
Dann wird das Histogramm anders erzeugt. Auf der Ordinatenachse wird dann nicht mehr die absolute Häufigkeit eingetragen, sondern die mithilfe der Klassenbreite gewichtete relative Häufigkeit. Genauer behandeln wir das im Abschnitt zu Histogrammen für unterschriedliche Klassenbreite.