Übung 4#
1. Ablesen der empirischen Verteilungsfunktion#
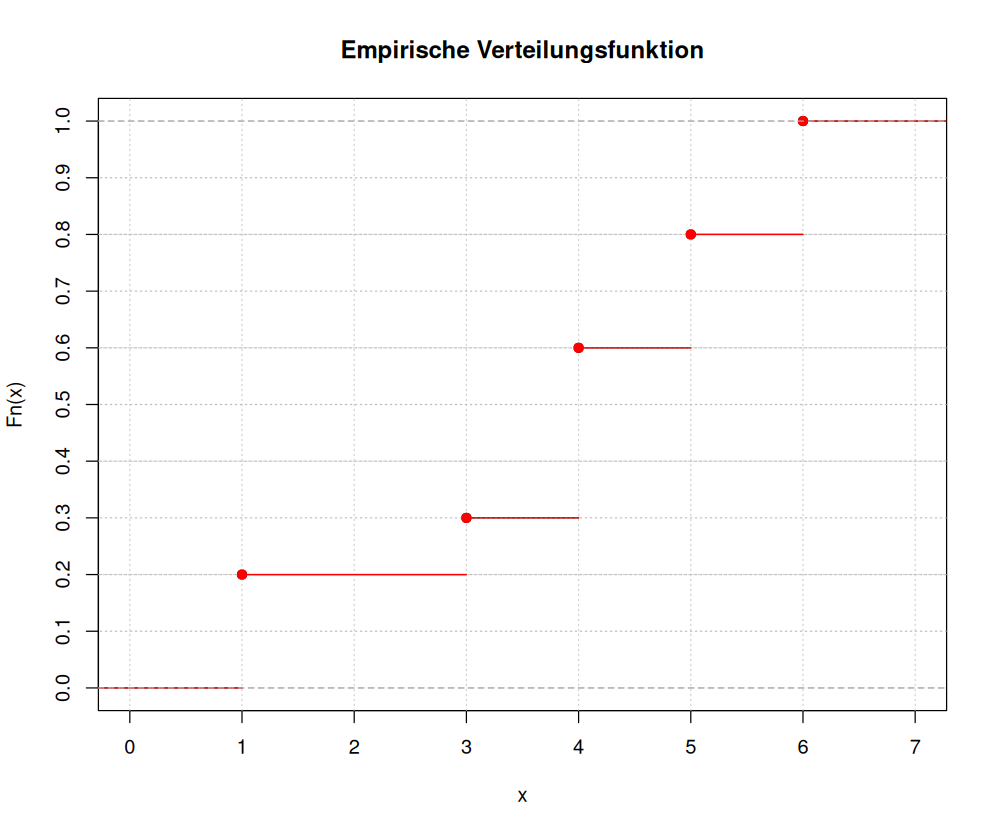
In der nächsten Grafik sehen Sie eine empirische Verteilungsfunktion. Beantworten Sie zur zugehörigen Stichprobe vom Umfang 80 die folgenden Fragen:
Wie viele Werte der Stichporobe gleich 5?
Wie viele Werte der Stichprobe sind gleich 2?
Wie viele Werte der Stichprobe sind größer als 3?
Bestimmen Sie den Modalwert der Stichprobe.
Berechnen Sie den Mittelwert und die Varianz der Stichprobe. (Lösung: 3.9, 2.926582)
2. Säulendiagramm und Kreisdiagramm#
Betrachten Sie den Datensatz HairEyeColor. Dieser ist vom Typ table und ist als 3-dimensionale (Häufigkeits-)Tabelle zu verstehen.
Verschaffen Sie sich einen Überblick über den Aufbau von
HairEyeColor. Nutzen Sie zum Beispielstr()oderHairEyeColor[1,,]oderHairEyeColor[,,1]oder … .Erstellen Sie ein Kreisdiagramm mit den Häufigkeiten der Haarfarben der Frauen. Passen Sie den Titel an. (Tipp:
rowSums()undcolSums())Erstellen Sie ein Säulendiagramm mit den Häufigkeiten der Haarfarben unter allen Personen. Passen Sie den Titel an.
Zusatz: Schreiben Sie über jede Säule die exakte Anzahl. Nutzen Sie dazu die Funktion
text().Erstellen Sie ein gestapeltes Säulendiagramm, in dem die Häufigkeiten der Haarfarben unter allen Personen angezeigt werden. Diese Säulen sollen in Abschnitte entsprechend der Augenfarben unterteilt werden.
Stellen Sie die Daten aus 5. mit einem gruppierten Säulendiagramm dar.
Was passiert, wenn Sie den Befehl
as.data.frame()nutzen umHairEyeColorin einendata.framezu überführen?
# Platz zum Rechnen
3. Konzentrationsmaße#
Die beiden Bäckereiketten Bäckerei Laugenland und Bäckerei Knack-Korn haben in Dresden verschiedene Filialen. Bäckerei Laugenland hat 12 Filialen und Bäckerei Knack-Korn hat 8 Filialen. Die Umsätze der einzelnen Filialen im letzten Monat sind hier aufgelistet:
Bäckerei Laugenland (Umsätze in 1.000 €):
Bäckerei Knack-Korn (Umsätze in 1.000 €):
Wir möchten (mit Hilfe von R) die Konzentration der Umsätze in den beiden Bäckereiketten untersuchen.
Skizzieren Sie die beiden Lorenzkurven (gemeinsam in ein Diagramm).
Berechnen Sie die beiden normierten Gini-Koeffizienten. (0.1108, 0.2675)
Berechnen Sie jeweils den Herfindahl-Index. (0.08597, 0.14995)
# Platz zum Rechnen
4. Datensätze einlesen#
CSV- und TXT-Dateien#
CSV (Comma Separated Values) und TXT (Textdateien) sind einfache Formate, um tabellarische Daten zu speichern. Sie bestehen aus Zeilen und Spalten, ähnlich wie in einer Tabelle.
Zeilen entsprechen in der Regel Beobachtungen (z. B. eine Person, ein Produkt, ein Zeitpunkt).
Spalten stehen meist für Variablen oder Merkmale (z. B. Alter, Preis, Datum).
Trennung der Daten#
Spaltentrenner: (Separator/Delimiter):
In CSV-Dateien: meist Komma (,)
Name,Alter,GehaltIn TXT-Dateien: oft Tabulator (\t) oder Semikolon (;)
Name;Alter;Gehalt
Zeilentrenner:
Normalerweise ein Zeilenumbruch (\n), also eine neue Zeile.
Dezimaltrenner:
In deutschsprachigen Dateien ist oft das Komma
,als Dezimaltrenner üblich (z. B. 3,14).In englischsprachigen Dateien ist es meistens der Punkt
.(z. B. 3.14).
Einlesen von CSV-/TXT-Dateien in R mit read.table()#
In R können solche Dateien mit read.table() eingelesen werden:
daten <- read.table("datei.csv", header = TRUE, sep = ",", dec = ".")
Die wichtigsten Argumente:
file: Pfad zur Datei (z. B. „daten.csv“)header = TRUE: erste Zeile enthält Spaltennamensep=: Spaltentrenner","falls,der Spaltentrenner ist (oft bei CSV)";"falls;der Spaltentrenner ist (oft bei Excel-CSV)"\t"falls die Spalten mit Tabulator getrennt sind
dec =: Dezimaltrenner"."falls in der einzulesenden Datei die englische Schreibweise für Dezimalzahlen genutzt wird","falls in der einzulesenden Datei die deutsche Schreibweise für Dezimalzahlen genutzt wird
Beispiele:
Deutsche CSV mit Semikolon und Komma als Dezimaltrenner:
daten <- read.table("daten.csv", header = TRUE, sep = ";", dec = ",")
TXT mit Tabulator als Trenner:
daten <- read.table("daten.txt", header = TRUE, sep = "\t", dec = ".")
XLS- und XLSX-Dateien#
In Mircosoft Excel oder ähnlichen Programmen werden die Dateien oft im Format xls oder xlsx abgelegt. Um solche Dateien in R einzulesen benötigt man das Paket readxl.
library("readxl")
Die Funktion zum Einlesen dieser Dateien heißt read_excel(). Die wichtigsten Argument sind:
path: Pfad zur Datei, z. B. „daten.xlsx“sheet: zum Festlegen, welches Tabellenblatt eingelesen werden soll. Angabe dur Name („Tabelle1“) oder Nummer (1)range: zum Festlegen des einzulesenden Zellbereichs, z.B. „A1:D10“col_names: Soll die erste Zeile als Spaltennamen verwendet werden? (TRUE/FALSE)col_types: Manuelle Angabe der Spaltentypen, z.B. c(„text“, „numeric“, „date“)na: Welche Zeichen sollen als fehlende Werte (NA) erkannt werden?
Das Format der eingelesen Daten ist dann tibble. Dies ist vergleichbar mit einem data.frame bietet allerdings ein paar mehr Möglichkeiten. Wollen sie dies wieder in ein data.frame transformieren, nutzen Sie as.data.frame().
Beispiele
Standardimport (erstes Blatt, erste Zeile als Spaltennamen):
daten <- read_excel("daten.xlsx")
Bestimmtes Tabellenblatt nach Name:
daten <- read_excel("daten.xlsx", sheet = "Umfrage2024")
Tabellenblatt nach Nummer (z. B. zweites Blatt):
daten <- read_excel("daten.xlsx", sheet = 2)
Nur bestimmten Zellbereich einlesen:
daten <- read_excel("daten.xlsx", range = "B3:E15")
Erste Zeile nicht als Spaltennamen verwenden:
daten <- read_excel("daten.xlsx", col_names = FALSE)
Fehlwerte definieren (z. B. leere Zellen oder „-„):
daten <- read_excel("daten.xlsx", na = c("", "-"))
Aufgaben#
Speichern Sie die Dateien
supermarket-sales.xlsx, sleep_health_lifestyle.txt, screentime.txt und air_pollution_china.csv
aus dem Ordner
in Ihrem Home-Verzeichnis.
Beachten Sie beim Einlesen der Dateien, ob Sie die richtigen Argumente genutzt haben. Schauen Sie sich die Dateien eingelesenen Datein mit head() und str() an um dies zu prüfen.
Lesen Sie die Datei
supermarket-sales.xlsxein. Schauen Sie diese zuvor in einer Tabellenkalkulationsprogramm an, um herauszufinden auf welchemsheetund in welchen Element der Tabelle die Daten zu finden sind.Berechnen Sie den Mittelwert und die Standardabweichung der Spalte
Retail Price (USD). (Lösung: 84.419, 57.044)Lesen Sie die Datei
sleep_health_lifestyle.txtein. Verwenden Sie die Argumenteheader=,sep=unddec=um entsprechende Werte richtig zu setzen.Berechnen Sie den Mittelwert der Schlafdauer. (Lösung: 7.132)
Erstellen Sie 4 Boxplots der Schlafdauer (einen für jede BMI-Kategorie)
Lesen Sie die Datei
screentime.txtein.Geben Sie die mittlere Bildschirmzeit für
MaleundFemalean. (Lösung: 3.07 und 2.92)Lesen Sie die Datei
air_pollution_china.csvein.Berechnen Sie Mittelwert und Varianz der Spalte
PM10..µg.m... (Lösung: 158.82 und 6547.27)
# Platz zum Rechnen


