\chi^2-Anpassungstest

\(\chi^2\)-Anpassungstest#

… ein parameterfreier Test zum Prüfen ob eine Stichporbe zu einer gegebenen Verteilung passt.

Bei der Durchführung des Tests halten wir uns and die bekannte Vorgehenweise. Im Folgenden werden die zugehörigen konkreten Hypothesen, Testgrößen, kritischen Bereiche und p-Werte besprochen.

Stetiger Fall#

Anhand einer Stichprobe \(X_1,\dots, X_n\) soll eine Annahme über die unbekannte Verteilungsfunktion \(F\) eines stetigen Merkmals \(X\) überprüft werden (z. B. \(X\) ist normalverteilt).

Gegeben / Vorbereitungen:#

  • Stichprobe der Größe \(n\):

    • mathematische Stichprobe: \(X_1, \dots, X_n\)

    • konkrete Stichprobe: \(x_1, \dots, x_n\)

  • Vermutete Verteilungsfunktion \(F_0\)
    (ggf. mit \(m\) geschätzten Parametern)

  • Einteilung der reellen Achse in \(k\) Klassen (Intervalle):

    \[ K_j = (a_j, a_{j+1}], \quad j = 1, \dots, k, \quad \text{mit } a_1 = -\infty,\, a_{k+1} = \infty \]

  • Wahrscheinlichkeiten unter \(F_0\):

    \[ p_j := \mathbb{P}_0(X \in K_j) = F_0(a_{j+1}) - F_0(a_j) \]

  • Beobachtete Häufigkeiten:
    \(H_j\) = Anzahl der Stichprobenwerte \(X_i\), die in \(K_j\) fallen

Testschritte#

  1. Signifikanzniveau wählen: \(\alpha \in (0,1)\)

  2. Hypothesen formulieren: \( H_0: F = F_0 \quad \text{vs.} \quad H_1: F \ne F_0\)
    (Dabei darf \(F_0\) geschätzte Parameter enthalten; Anzahl: \(m\))

  3. Testgröße:

    \[ T = \sum_{j=1}^k \frac{(H_j - n p_j)^2}{n p_j} \]

    Unter der Nullhypothese gilt:

    \[ T \stackrel{a}{\sim} \chi^2(k - m - 1) \]

    In Worten: T ist asymptotisch \(\chi^2\)-verteilt mit Parameter \(k-m-1\)

    Hierbei ist:

    • \(n\): Stichprobengröße

    • \(k\): Anzahl der Klassen

    • \(m\): Anzahl der geschätzten Parameter

    Konkreter Testwert:

    \[ t = \sum_{j=1}^k \frac{(h_j - n p_j)^2}{n p_j} \]

    wobei \(h_j\) die Anzahl der Werte der konkreten Stichprobe im Intervall \(K_j=(a_j,a_{j+1}]\) ist

  4. Kritischer Bereich:

    Der kritische Bereich \(K\) ist so gewählt, dass:

    \[ \mathbb{P}_0(T \in K) \leq \alpha \]

    Setze also:

    \[ K = \left( \chi^2_{k - m - 1,\; 1 - \alpha},\; \infty \right) \]

  5. Entscheidungsregel:

    • Falls \(t \in K\):
      Nullhypothese \(H_0\) wird abgelehnt
      → Der Test ist signifikant

    • Falls \(t \notin K\):
      Keine ausreichenden Hinweise gegen \(H_0\)
      → Der Test ist nicht signifikant

Bemerkungen zum \(\chi^2\)-Anpassungstest#

  • Die Verteilungsfunktion \(F_0\) ist eine zuvor festgelegte, vollständig bekannte Verteilungsfunktion (bis auf evtl zu schätzende Parameter).

    Die Anzahl der geschätzten Parameter ist \(m\).

  • Die Testgröße

    \[ T = \sum_{j=1}^k \frac{(\mathbf{H}_j - n p_j)^2}{n p_j} \stackrel{a}{\sim} \chi^2(k - m - 1) \]

    ist „groß“, wenn die beobachteten Häufigkeiten \(H_j\) stark von den theoretischen Häufigkeiten \(n p_j\) abweichen.
    Daher liegt der kritische Bereich rechts:

    \[ K = \left( \chi^2_{k - 1 - m,\; 1 - \alpha},\; \infty \right) \]

    Große Werte von \(T\) sprechen gegen die Nullhypothese.

  • Die Teststatistik \(T\) ist asymptotisch \(\chi^2\)-verteilt.
    Wir nutzen die folgende Faustregel für die Anwendbarkeit des Verfahrens:

    \[ \boxed{n p_j \geq 5 \qquad \text{für alle}\quad j = 1, \dots, k} \]

  • Eventuell unbekannte Parameter sind nach dem Maximum-Likelihood-Prinzip zu schätzen. Da wir dieses Verfahren hier nicht behandeln, geben wir bei Aufgaben im Rahmen der Vorlesung die passenden Schätzfunktionen mit an.

Berechnung des p-Werts#

  • Der p-Wert ist die Wahrscheinlichkeit, unter der Nullhypothese \(H_0\) einen Testwert, welcher mindestens so extrem ist wie der beobachtete Wert \(t\), zu erhalten:

    \[ \text{p-Wert} = \mathbb P_0(T \geq t) = 1 - F_{\chi^2(k - m - 1)}(t) \]

  • In R kann der p-Wert mit der Funktion pchisq() berechnet werden:

    pchisq(t, df = k - m - 1, lower.tail = FALSE)

    oder

    1 - pchisq(t, df = k - m - 1)

    Dabei ist:

    • t der beobachtete Testwert,

    • df = k - m - 1 die Anzahl der Freiheitsgrade,

    • lower.tail = FALSE oder 1 - ..., weil der kritische Bereich rechts liegt.

Diskreter Fall#

Anhand einer Stichprobe \(X_1,\dots,X_n\) soll eine Annahme über die unbekannte Verteilungsfunktion \(F\) (nicht nur Parameter unbekannt) des diskreten Merkmals \(X\) überprüft werden. Beispielsweise:

  • man möchte man wissen, ob ein Merkmal \(X\) auf \(\{1,2,3,4\}\) gleichverteilt ist; oder

  • man möchte wissen, ob \(X\) auf \(\{1,2,\dots, N\}\) gleichverteilt ist.

Im zweiten Fall muss \(N\) zunächst geschätzt werden. Dann wird im Test mit dem Schätzwert für \(N\) gearbeitet und es wird einbezogen, dass \(m=1\) Parameter geschätzt wurde.

Gegeben / Vorbereitungen:#

  • Stichprobe der Größe \(n\):

    • mathematische Stichprobe: \(X_1, \dots, X_n\)

    • konkrete Stichprobe: \(x_1, \dots, x_n\)

  • vermutete Verteilungsfunktion \(F_0\) (mit \(m\) geschätzten Parametern) und zugehörige Verteilungstabelle:

    Wert

    \(x_1\)

    \(x_2\)

    …

    \(x_k\)

    Wahrscheinlichkeit

    \(p_1\)

    \(p_2\)

    …

    \(p_k\)

  • \(H_j\) … Anzahl der Stichprobenwerte \(X_i\) mit Wert \(x_j\)

Beachte:

  • Das Vorgehenist fast wie im stetigen Fall, aber die Klassen sind hier einelementig.

  • Wieder ist zu überprüfen, ob \(np_j \geq 5\) für alle \(j = 1, \dots, k\) gilt.
    Falls dies nicht der Fall ist und \(X\) ordinal messbar ist, so kann man benachbarte Elemente zu Klassen zusammenfassen, damit die Faustregel erfüllt wird.

Testschritte#

  1. Wahl des Signifikanzniveaus \(\alpha \in (0, 1)\)

  2. Aufstellen einer (Null-)Hypothese
    \(H_0: F = F_0\), \(H_1: F \neq F_0\)
    (Die vermutete Verteilung \(F_0\) darf geschätzte Parameter enthalten, Anzahl \(m\).)

  3. Testgröße \(T\) mit bekannter Verteilung unter \(H_0\):

    \[ T = \sum_{j=1}^k \frac{(H_j - n p_j)^2}{n p_j} \stackrel{a}{\sim} \chi^2(k - m - 1) \]

    Der konkrete Testwert \(t\) wird auf Basis der konkreten Stichprobe \(x_1, \dots, x_n\) berechnet.

  4. Kritischer Bereich \(K\) mit der Eigenschaft \(\mathbb{P}_0(T \in K) \leq \alpha\).
    Dafür setzen wir:

    \[ K := \left( \chi^2_{k - m - 1, 1 - \alpha}, \infty \right) \]

  5. Entscheidungsregel:

    • Fall \(t \in K\): Ablehnung der Nullhypothese \(H_0\)
      → Der Test ist signifikant

    • Fall \(t \notin K\): Auf Basis des Tests ist nichts gegen \(H_0\) einzuwenden
      → Der Test ist nicht signifikant

Berechnung des p-Werts#

  • Der p-Wert ist die Wahrscheinlichkeit, unter der Nullhypothese \(H_0\) einen Testwert zu erhalten, welcher mindestens so extrem wie der beobachtete Wert \(t\):

    \[ \text{p-Wert} = \mathbb{P}_0(T \geq t) = 1 - F_{\chi^2(k - m - 1)}(t) \]

  • In R kann der p-Wert mit der Funktion pchisq() berechnet werden:

    pchisq(t, df = k - m - 1, lower.tail = FALSE)

    oder

    1 - pchisq(t, df = k - m - 1)

    Dabei ist:

    • t der beobachtete Testwert,

    • df = k - m - 1 die Anzahl der Freiheitsgrade,

    • lower.tail = FALSE oder 1 - ..., weil der kritische Bereich rechts liegt.

Beispiele#

Beispiel: Stetiger Fall#

Bei 100 Bauelementen der gleichen Art wurde die Lebensdauer überprüft. Eine statistische Auswertung ergab:

  1. \(\bar{x} = 1203.1\) [h], \(s = 614.9\) [h]

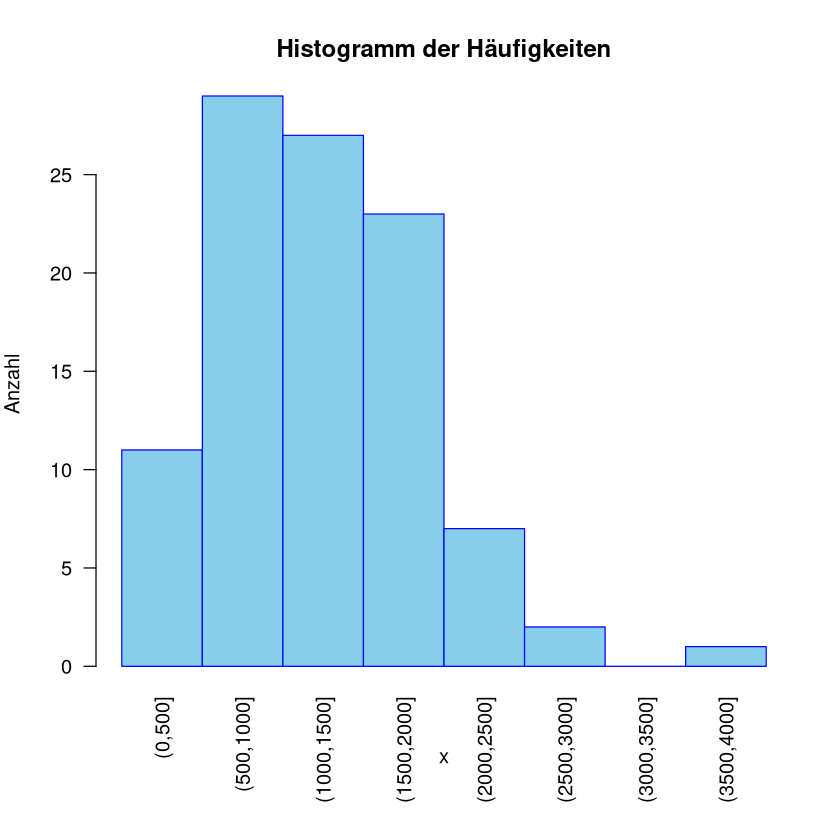
  2. Häufigkeitstabelle und Histogramm

Klasse

Anzahl

\([0,500]\)

11

\((500,1000]\)

29

\((1000,1500]\)

27

\((1500,2000]\)

23

\((2000,2500]\)

7

\((2500,3000]\)

2

\((3000,3500]\)

0

\((3500,4000]\)

1
Hide code cell source 
# Klassenuntergrenzen und -obergrenzen
breaks <- c(0, 500, 1000, 1500, 2000, 2500, 3000, 3500, 4000)

# Häufigkeiten pro Klasse
counts <- c(11, 29, 27, 23, 7, 2, 0, 1)

# Klassenbezeichnungen
class_labels <- paste0("(", head(breaks, -1), ",", tail(breaks, -1), "]")

# Layout anpassen: mehr Platz unten (mar = c(unten, links, oben, rechts))
par(mar = c(7, 4, 4, 2))  # Standard ist c(5,4,4,2)

# Balkendiagramm zeichnen
barplot(height = counts,
        names.arg = class_labels,
        space = 0,
        col = "skyblue",
        xlab = "x",
        ylab = "Anzahl",
        main = "Histogramm der Häufigkeiten",
        border = "blue",
        las = 2)  # las = 2 -> senkrechte Beschriftung der Klassen
../_images/a49f6c43f409e5abf89cfb1f5d9bdf5babd63f9098b1db8f84b193ec06673bd6.png

Es ist mit einem Signifikanzniveau von \(0.05\) zu überprüfen, ob das Merkmal \(X\) als exponentialverteilt angesehen werden kann.

Hinweis: Der ML-Schätzer für \(\lambda\) ist \(\hat{\lambda} = \frac{1}{\bar{x}}\).

Lösung#

  1. Signifikanzniveau: \(\alpha = 0.05\)

  2. Hypothesen:

    \[\begin{split} H_0: F = F_0 \quad \text{mit} \quad F_0(x) = \begin{cases} 1 - \exp(-\lambda x), & x \geq 0 \\ 0, & \text{sonst} \end{cases} \end{split}\]

    Also \(X \sim \mathrm{Exp}(\lambda)\).

    Der ML-Schätzer ist \(\hat\lambda = \frac{1}{1203.1} = 8.312 \cdot 10^{-4}\).

  3. Testgröße:

    \(j\)

    \(K_j = [a_j, a_{j+1})\)

    \(F_0(a_j)\)

    \(p_j = F_0(a_{j+1}) - F_0(a_j)\)

    \(n p_j\)

    \(h_j\)

    1

    \([0,500]\)

    0

    0.340

    34.0

    11

    2

    \((500,1000]\)

    0.340

    0.224

    22.4

    29

    3

    \((1000,1500]\)

    0.564

    0.149

    14.9

    27

    4

    \((1500,2000]\)

    0.713

    0.097

    9.7

    23

    5

    \((2000,2500]\)

    0.810

    0.065

    6.5

    7

    6

    \((2500,3000]\)

    0.875

    0.042

    4.2

    2

    7

    \((3000,3500]\)

    0.917

    0.028

    2.8

    0

    8

    \((3500, \infty)\)

    0.945

    0.055

    5.5

    1

    Achtung: Bedingung \(n p_j \geq 5\) verletzt!

    → Fasse Zeilen \(j=6\) und \(j=7\) zusammen.

    Neue Tabelle:

    \(j\)

    \(K_j = [a_j, a_{j+1})\)

    \(F_0(a_j)\)

    \(p_j = F_0(a_{j+1}) - F_0(a_j)\)

    \(n p_j\)

    \(h_j\)

    1

    \([0,500]\)

    0

    0.340

    34.0

    11

    2

    \((500,1000]\)

    0.340

    0.224

    22.4

    29

    3

    \((1000,1500]\)

    0.564

    0.149

    14.9

    27

    4

    \((1500,2000]\)

    0.713

    0.097

    9.7

    23

    5

    \((2000,2500]\)

    0.810

    0.065

    6.5

    7

    6

    \((2500,3500]\)

    0.875

    0.070

    7.0

    2

    7

    \((3500, \infty)\)

    0.945

    0.055

    5.5

    1

    Testgröße lautet daher:

    \[ T = \sum_{j=1}^7 \frac{(H_j - n p_j)^2}{n p_j} \stackrel{a}{\sim} \chi^2(7 - 1 - 1) \quad \text{falls } H_0 \text{ wahr ist} \]

    Konkreter Wert der Testgröße \(t\):

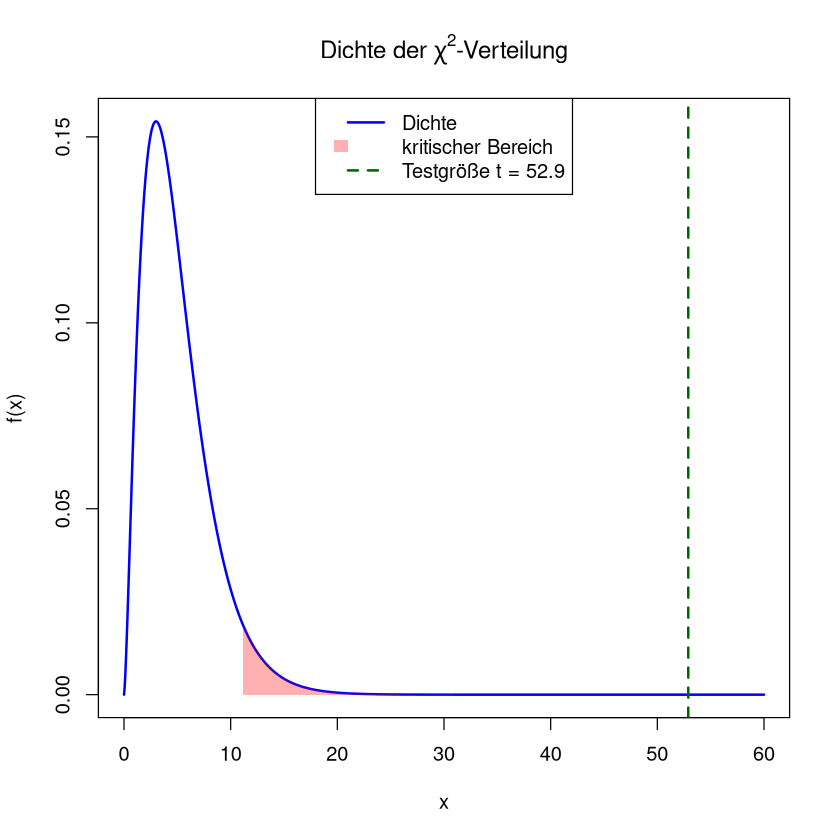
    \[ t = \sum_{j=1}^7 \frac{(h_j - n p_j)^2}{n p_j} = \frac{(11-34.0)^2}{34.0} + \frac{(29-22.4)^2}{22.4} + \dots + \frac{(1-5.5)^2}{5.5} = 52.9 \]

  4. Kritischer Bereich:

    \[ K = (\chi^2_{5,0.95}, \infty) = (11.07, \infty) \]

  5. Testentscheidung:

    \[ t \in K \qquad\Rightarrow \qquad H_0 \text{ wird abgelehnt } \]

  6. Interpretation:

    Die Hypothese, dass die Lebensdauer der Bauelemente exponentialverteilt ist, ist (bei einem Signifikanzniveau von 0.05) zu verwerfen.

Hide code cell source 
# Parameter
df       <- 5       # Freiheitsgrade 
t        <- 52.9    # Testgröße
kritisch <- 11.07   # Beginn des kritischen Bereichs

# x-Werte für die Dichte
x <- seq(0, max(t, 60), length.out = 1000)

# Dichte der Chi-Quadrat-Verteilung
y <- dchisq(x, df)

# Plot
plot(x, y, type = "l", lwd = 2, col = "blue",
     xlab = "x", ylab = "f(x)",
     main = expression(paste("Dichte der ", chi^2, "-Verteilung")))

# Kritischen Bereich einfärben
polygon(c(x[x >= kritisch], rev(x[x >= kritisch])),
        c(y[x >= kritisch], rep(0, sum(x >= kritisch))),
        col = rgb(1, 0, 0, 0.3), border = NA)

# Testgröße als vertikale Linie
abline(v = t, col = "darkgreen", lwd = 2, lty = 2)

# Legende
legend("top", legend = c("Dichte", "kritischer Bereich", "Testgröße t = 52.9"),
       col = c("blue", rgb(1, 0, 0, 0.3), "darkgreen"),
       lwd = c(2, NA, 2), lty = c(1, NA, 2),
       fill = c(NA, rgb(1, 0, 0, 0.3), NA),
       border = c(NA, NA, NA))
../_images/3a15796b9176f162665bcf249f880f77e2956b43705afb80b25e47c0ff6ec3a2.png

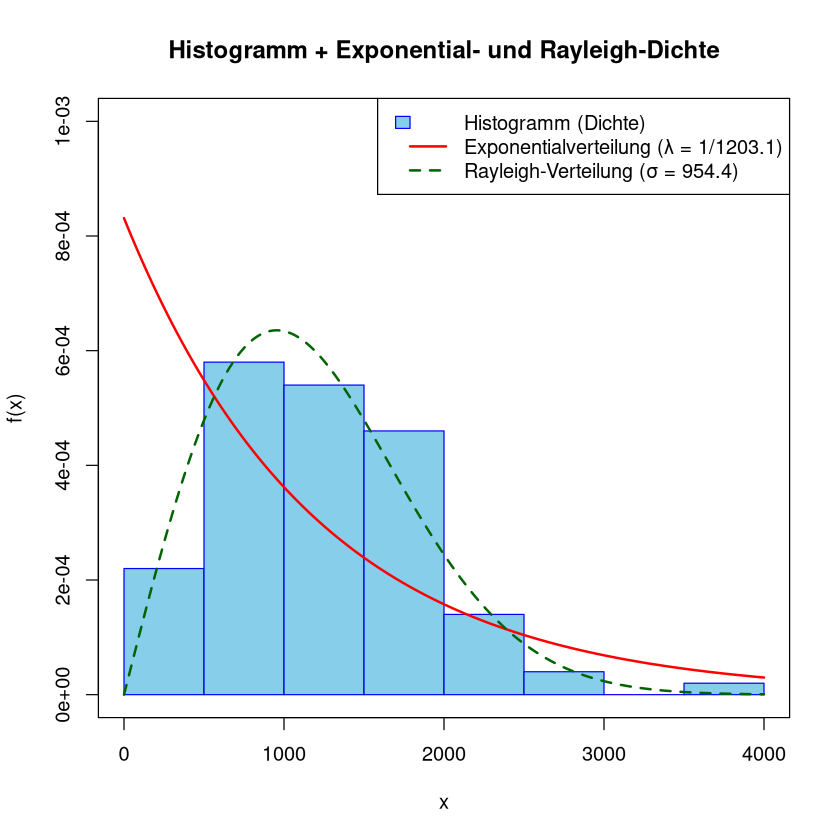
Bemerkungen zum Beispiel#

  • Das Histogramm passt auch optisch nicht so gut zur Dichte der Exponentialverteilung (rote Funktion).

  • Anders sieht das mit der Dichte der Rayleigh-Verteilung (grüne Funktion) aus, siehe zum Beispiel Wikipedia

  • Führt man den \(\chi^2\)-Anpassungstest mit der Rayleigh-Verteilung aus, so wird die Nullhypothese nicht abgelehnt.

  • Beachte: Die Exponentialverteilung und die Rayleigh-Verteilung sind beides Spezialfälle der Weibull-Verteilung (mit Parameter \(k=1\) bzw. \(k=2\)), siehe zum Beispiel Wikipedia

Hide code cell source 
#  Gegeben ist:
n      <- 100            # Stichprobengroesse
barx   <- 1203.1         # Mittelwert
s      <- 614.9          # emp. Stdabw

# Lambda fuer Exp-Vert. schaetzen
lambda <- 1/1203.1       # gesch. lambda fuer Exp-vert

# ML-Schaetzwert fuer Rayleigh-Verteilung aus barx und s
ssq    <- (n-1)*(s^2+n/(n-1) * barx^2)  # sum of squares, sum x_i^2
sigma  <- sqrt(1/(2*n) *ssq )           # gesch. Parameter Rayleigh   

# Klassenuntergrenzen und -obergrenzen
breaks <- c(0, 500, 1000, 1500, 2000, 2500, 3000, 3500, 4000)

# Häufigkeiten
counts <- c(11, 29, 27, 23, 7, 2, 0, 1)

# Klassenbreiten
widths <- diff(breaks)

# Dichte = rel.Häufigkeit / Klassenbreite
densities <- counts / widths /100

# Leeres Plot-Fenster vorbereiten (mit y-Achse für Dichte)
plot(NA, xlim = c(0, 4000), ylim = c(0, max(densities, 0.001)),
     xlab = "x", ylab = "f(x)",
     main = "Histogramm + Exponential- und Rayleigh-Dichte")

# Histogramm zeichnen
for (i in 1:length(densities)) {
  rect(xleft = breaks[i],
       xright = breaks[i + 1],
       ybottom = 0,
       ytop = densities[i],
       col = "skyblue",
       border = "blue")
}

# x-Werte für Dichtefunktionen
xvals <- seq(0, 4000, length.out = 1000)

# Exponentialverteilung: lambda = 1 / Mittelwert
exp_density <- dexp(xvals, rate = lambda)
lines(xvals, exp_density, col = "red", lwd = 2)

# Rayleigh-Verteilung: sigma = geschaetzt, siehe oben
rayleigh_density <- (xvals / sigma^2) * exp(-(xvals^2) / (2 * sigma^2))
lines(xvals, rayleigh_density, col = "darkgreen", lwd = 2, lty = 2)

# Legende
legend("topright",
       legend = c("Histogramm (Dichte)", 
                  "Exponentialverteilung (λ = 1/1203.1)",
                  "Rayleigh-Verteilung (σ = 954.4)"),
       fill = c("skyblue", NA, NA),
       border = c("blue", NA, NA),
       lty = c(NA, 1, 2),
       lwd = c(NA, 2, 2),
       col = c("skyblue", "red", "darkgreen"))
../_images/7887b9bbb29335fe4503c635d1863bd837b6f1f30b947af4901d2ac9018d8d95.png

Beispiel: Diskreter Fall#

Um besser planen zu können, soll in einem Call-Center die Verteilung der Anrufe untersucht werden.
Eine Stichprobe von 100 Intervallen zu je 3 Minuten ergab:

Anzahl der Anrufe

0

1

2

3

4

\(\geq\) 5

Häufigkeit der Intervalle mit dieser Anzahl an Anrufen

7

14

20

18

26

15

\(n \cdot p_j\) (unter Annahme Poissonverteilung)

5.03

15.04

22.48

22.40

16.75

18.30

Im Mittel riefen 2.99 Personen pro Intervall an.

Führen Sie einen Test mit der Nullhypothese
„die Anzahl der Anrufe in einem 3-Minuten-Intervall ist poissonverteilt“
zum Signifikanzniveau 0.05 durch.

Hinweis: ML-Schätzung des Parameters der Poissonverteilung: \(\hat{\lambda} = \bar{x}\)

Lösung#

  • \(F\) … tatsächliche Verteilungsfunktion

  • \(F_0\) … Verteilungsfunktion der Poissonverteilung mit \(\lambda = \bar{x} = 2.99\)

Berechne für \(X\) (falls es mit \(F_0\) verteilt ist):

\[ p_1 = \mathbb P(X=0), \quad \dots \quad, p_5 = \mathbb P(X=4), \quad p_6 = \mathbb P(X \geq 5) \]

Durchführung des Tests

  1. Signifikanzniveau: \(\alpha = 0.05\)

  2. Hypothesen:

    \[ H_0: F = F_0, \qquad H_1: F \neq F_0 \]

  3. Testgröße:

    \[ T = \sum_{j=1}^6 \frac{(H_j - n p_j)^2}{n p_j} \]

    Konkreter Wert der Testgröße:

    \[ t = \frac{(7 - 5.03)^2}{5.03} + \dots + \frac{(15 - 18.3)^2}{18.3} = 7.684637 \]

  4. Kritischer Bereich:

    \[ K = \left(\chi^2_{6-1-1, 0.95}, \infty\right) = (9.4877, \infty) \]

  5. Testentscheidung:

    \[ t \notin K \implies H_0 \text{ wird nicht verworfen} \]

  6. Interpretation:
    Die Hypothese, dass die Daten poissonverteilt sind, ist (bei einem Signifikanzniveau von 0.05) nicht zu verwerfen.
    Die vorliegenden Daten sprechen nicht gegen die Poissonverteilung.

Bemerkung zum Beispiel#

Mit dem Test wurde nicht gezeigt, dass die Daten tatsächlich poissonverteilt sind!

Die Daten sprechen nur nicht so stark gegen die Poissonverteilung, dass wir sie (zu \(\alpha=0.05\)) ablehnen müssen.

Umsetzung mit chisq.test#

Besonders schnell lässt sich dieser Test in R umsetzen, wenn man die Funktion chisq.test nutzt.

Man benötigt dafür:

  • Einen Vektor mit den beobachteten Häufigkeiten.

  • Optional: Einen Vektor mit den erwarteten Häufigkeiten oder Wahrscheinlichkeiten. Fehlt dieser, wird gegen die Gleichverteilung getestet.

chisq.test(x = beobachtet, p = erwartete_Wahrscheinlichkeiten)

Hier muss in beobachtet der Vektor der beobachteten Häufigkeiten stehen. Der Vektor erwartete_Wahrscheinlichkeiten enthält die, wie der Name schon sagt, die erwarteten Wahrscheinlichkeiten für die verschiedenen Klassen. Die getestestete Nullhypothese ist also: Die wahren Wahrscheinlichkeiten sind die in erwartete_Wahrscheinlichkeiten.

Schreibt man

chisq.test(beobachtet)

So wird gegen die Gleichverteilung getestet, d.h. \(H_0:\) das Merkmal ist gleichverteilt; \(H_1:\) das Merkmal ist nicht gleichverteilt

Beispiel 1#

Wollen wir den p-Wert für das Beispiel zum stetigen Fall berechnen, so ist folgendes einzugeben

# beobachtete Häufigkeiten
beob <- c(11, 29, 27, 23, 7, 2, 1)

# erwaretete Wahrscheinlichkeiten
prob <- c(0.340, 0.224, 0.149, 0.097, 0.065, 0.070, 0.055)  

# Berechnung von Testgroesse und p-Wert
chisq.test(x=beob, p=prob)

	Chi-squared test for given probabilities

data:  beob
X-squared = 52.857, df = 6, p-value = 1.253e-09

Der p-Wert ist kleiner als 0.05 (das Signifikanzniveau des Beispeils), daher lehnen wir die Nullhypothese, dass die Daten exponentialverteilt sind ab.

Beispiel 2#

Wollen wir den p-Wert für das Beispiel zum diskreten Fall berechnen, so ist folgendes einzugeben

# beobachtete Häufigkeiten
beob <- c(7, 14, 20, 18, 26, 15)  

# erwaretete Wahrscheinlichkeiten
v<-dpois(0:4,lambda = 2.99)
prob <- c(v,1-sum(v))
prob

# Berechnung von Testgroesse und p-Wert
chisq.test(x=beob, p=prob)
  1. 0.0502874367235919
  2. 0.15035943580354
  3. 0.224787356526292
  4. 0.224038065337871
  5. 0.167468453840059
  6. 0.183059251768647
	Chi-squared test for given probabilities

data:  beob
X-squared = 7.6928, df = 5, p-value = 0.174

Der p-Wert ist nicht kleiner als 0.05 (das Signifikanzniveau des Beispeils), daher lehnen wir die Nullhypothese, dass die Anzahl der Fehler poissonverteilt ist nicht ab.