Klassierung 2.0#
Haben wir eine Stichprobe vorliegen mit sehr vielen Ausprägungen, so ist es für verschiedene Anwendungen wichtig diese Daten in Klassen einzuteilen. Man spricht dann von Klassierung.
Dies tritt typischerweise auf bei stetigen Merkmalen (z.B Messung von Körpergröße, Einkommen, …). Wir haben dazu bereits im Abschnitt Klassierung von Daten gelernt wie man bei der Klassierung typischerweise vorgeht, wie man die Klassen wählt und die Klassenhäufigkeiten in einem Histogramm darstellt. Dabei haben wir uns auf den Fall beschränkt, dass alle Klassen gleich breit sind.
Im folgenden schauen wir uns an,
wie Histogramme gebildet werden, wenn die Klassen unterschiedliche Breiten haben;
wie Verteilungsfunktionen gebildet werden, wenn die Daten nur klassiert vorliegen.
Histogramme bei unterschiedlichen Klassenbreiten#
In diesem Kapitel beschäftigen wir uns mit Klassierten Daten und deren Darstellung im Fall von unterschiedlichen Klassenbreiten.
Erinnerung: Sind unsere Daten in Klassen gleicher Breite eingeteilt, so ist die Darstellung als Histogramm schneller erklärt und durchgeführt:
jede Klasse bekommt eine Säule
die Breite jeder Säule ist gleich der Klassenbreite
die Höhe der einer Säule ist gleich der absoluten Häufigkeit der Klasse
Definition#
Definition
Liegen Daten in klassierter Form vor und sind die Klassen unterschiedlich breit, so wird ein Histogramm folgendermaßen erstellt:
jede Klasse bekommt eine Säule
die Breite der Säule ist gleich der Klassenbreite
die Höhe der Säule ist gleich relativen Häufigkeit geteilt durch die Klassenbreiten
Sind die Klassen \((a_0,a_1], (a_1,a_2], \dots (a_{k-1}, a_k]\) und die relative Häufigkeiten \(f_1, f_2,\dots f_k\), so ist die Höhe der Säule
Der Wert \(d_i\) heißt Häufigkeitsdichte der Klasse \(i\).
Erklärung#
Stellen wir uns für einen Moment vor, dass wir eine Stichprobe erheben welche nur „zufälligerweise“ aus den Zahlen
besteht. Die Stichprobe ist also ganz gleichmäßig in dem Intervall von 1 bis 100 verteilt. In einem Histogramm wollen wir dann auch sehen, dass alle Säulen gleich hoch sind um uns diese spezielle Verteilung zu visualisieren. Teilen wir die Daten in die 10 Klassen \((0,10], (10,20], \dots (90,100]\) auf, erhalten wir die Häufigkeiten:
Klasse |
\((0,10]\) |
\((10,20]\) |
\((20,30]\) |
\((30,40]\) |
\((40,50]\) |
\((50,60]\) |
\((60,70]\) |
\((70,80]\) |
\((80,90]\) |
\((90,100]\) |
absolute Häufigkeit |
\(10\) |
\(10\) |
\(10\) |
\(10\) |
\(10\) |
\(10\) |
\(10\) |
\(10\) |
\(10\) |
\(10\) |
Tragen wir an jeder Säule die absolute Häufigkeit (\(=10\)) ab, so sehen wir 10 gleich hohe Säulen.
Show code cell source
x <- 1:100
hist(x,main="Histogramm bei gleicher Klassenbreite")
Was passiert aber wenn die Klassen nicht gleich bereit wählen, sondern z.B. die Einteilung
vorliegt? Dann hätten wir die Häufigkeitstabelle
Klasse |
\((0,10]\) |
\((10,50]\) |
\((50,100]\) |
absolute Häufigkeit |
\(10\) |
\(40\) |
\(50\) |
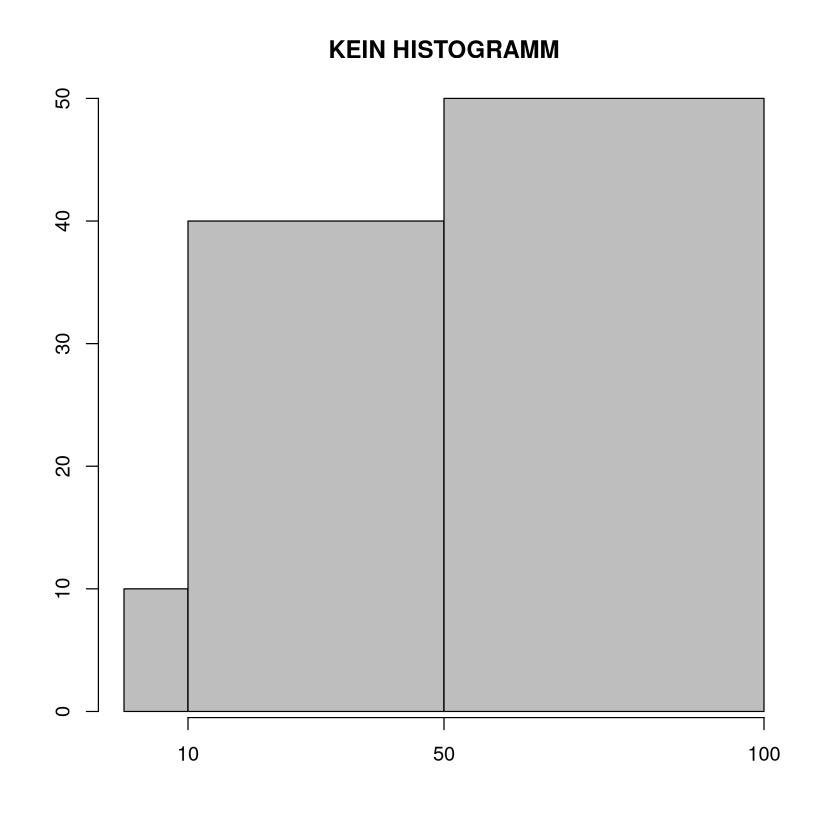
Ein Säulendiagramm in dem die Höhen die abhsolute Häufigkeit ist, stellt die „ganz gleichmäßige Verteilung“ der Stichprobe offensichtlich nicht richtig dar.
Show code cell source
# Daten erstellen
x <- c(10, 40, 50) # Höhen der Säulen
y <- c(10, 40, 50) # Breiten der Säulen
tics <- c(10,50,100) # Stellen an denen die x-Achse beschriftet wird
# Barplot erstellen
barplot(height=x,width=y, space=0, xaxt="n",main="KEIN HISTOGRAMM")
# x-Achse mit Zahlen und Ticks versehen
axis(1, at=tics, labels=tics)#
Diese Grafik vermittelt den optischen Eindruck, dass es mehr große als kleine Werte in der Stichprobe gibt. Der Grund für diese Verzerrung ist, dass große Klassen „im Vorteil“ sind und hier wegen ihrer Breite mehr Elemente enthalten. Dies wird repariert, indem man (wie in der Definition beschrieben) die Häufigkeiten durch die Klassenbreite teilt. Der so erhaltene Wert drückt die relative Häufigkeit pro Einheit auf der x-Achse aus und ist damit eine Art Dichte. Folglich heißt der errechnete Wert \( d_i= \frac{f_i}{a_i-a_{i-1}}\) auch Häufigkeitsdichte.
Umsetzung in R#
Beispiel 1#
Hier nutzen wir den Befehl hist(). Der erste Eintrag in Klammern muss die Stichprobe sein. Der zweite Eintrag legt fest an welchen Stellen unterteilt wird.
x<-1:100 # Eingabe der Stichprobe
hist(x,c(0,10,50,100)) # Erstellt das Histogramm
Beispiel 2#
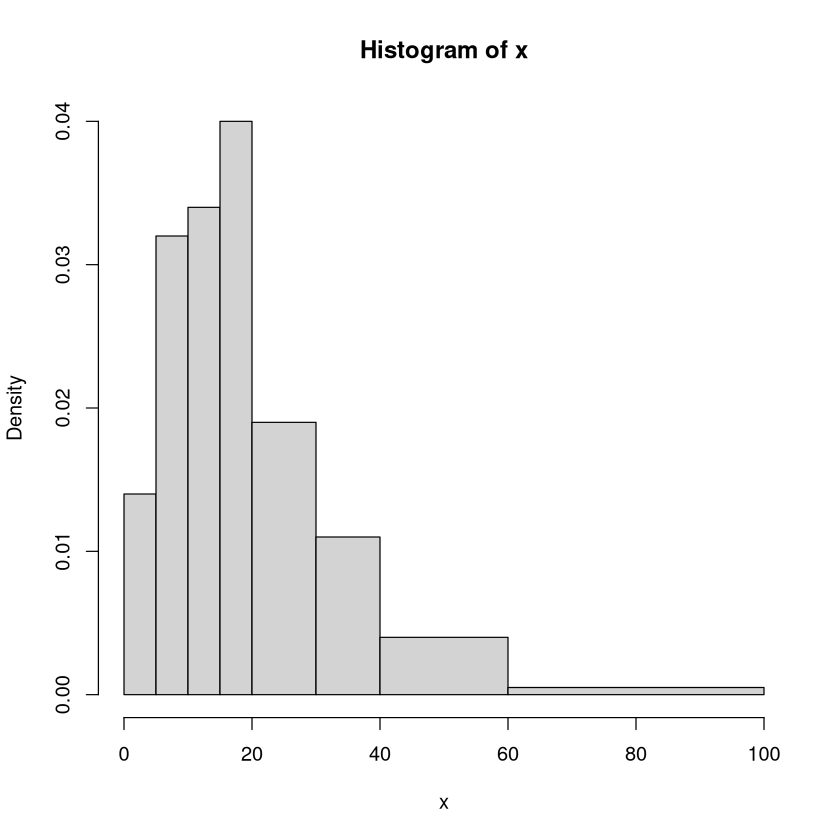
Ein etwas spannenderes Beispiel mit zufällig erzeugten Daten: Wir erzeugen eine zufällige Stichprobe, teilen die Daten in Klassen (unterschiedlicher Breite) ein und erstellen ein Histogramm. Zusätzlich wird eine Tabelle erzeugt in der die Häufigkeitsdichten (also die Höhen der Säulen) stehen.
set.seed(234) #hält den Zufall fest
x <- rweibull(100,shape = 1.4, scale = 25) #zufällige Daten erzeugen
og <- ceiling(max(x)/10)*10 #das maximale Element auf den nächsten vollen Zehner aufrunden
breaks <- c(0,5,10,15,20,30,40,60,og) #die breaks erstellen
# Histogramm erstellen
hist(x,breaks)
# Berechnung der Häufigkeitsdichte
breite <- breaks[-1] - breaks[-length(breaks)] #vektor mit Abständen zw. breaks erstellen
abs.h <- table(cut(x , breaks)) #abs.Häufigkeiten der klassierten Daten
rel.h <- abs.h/length(x) #rel.Häufigkeiten der klassierten Daten
# Ausgabe der Häufigkeitsdichte Werte
cat("Häufigkeitsdichte:")
rel.h/breite #rel.Häufigkeit / Klassenbreite
# Hübsche Tabelle erstellen:
# rbind klebt die 3 Zeilen aneinander, Ergebnis ist eine Matrix
tabelle <- rbind(abs.h,rel.h,rel.h/breite)
# ändern der Spaltennamen
dimnames(tabelle)[[1]] <- c("abs.Häufigkeit","rel.Häufigkeit","Häufigkeitsdichte")
# Ausgabe der Tabelle
tabelle
Häufigkeitsdichte:
(0,5] (5,10] (10,15] (15,20] (20,30] (30,40] (40,60] (60,100]
0.0140 0.0320 0.0340 0.0400 0.0190 0.0110 0.0040 0.0005
| (0,5] | (5,10] | (10,15] | (15,20] | (20,30] | (30,40] | (40,60] | (60,100] | |
|---|---|---|---|---|---|---|---|---|
| abs.Häufigkeit | 7.000 | 16.000 | 17.000 | 20.00 | 19.000 | 11.000 | 8.000 | 2e+00 |
| rel.Häufigkeit | 0.070 | 0.160 | 0.170 | 0.20 | 0.190 | 0.110 | 0.080 | 2e-02 |
| Häufigkeitsdichte | 0.014 | 0.032 | 0.034 | 0.04 | 0.019 | 0.011 | 0.004 | 5e-04 |
Verteilungsfunktionen bei klassierten Daten#
Hier stellen wir uns vor wir kennen nur die klassierten Daten und nicht den Ausgangsdatensatz. Dann können wir nicht wie üblich die Verteilungsfunktion erstellen (da wir nicht wissen an welchen Stellen sie spingen muss). In einer solchen Situation kann man sich behelfen mit einer Verteilungsfunktion, welche „möglichst nah“ an der richtigen dran ist. Um zu verstehen wie diese gebildet wird, schauen wir uns ein Beispiel an
Klasse |
\((0,10]\) |
\((10,20]\) |
\((20,30]\) |
\((30,40]\) |
absolute Häufigkeit |
\(20\) |
\(10\) |
\(50\) |
\(20\) |
relative Häufigkeit |
\(\frac{1}{5}\) |
\(\frac{1}{10}\) |
\(\frac12\) |
\(\frac15\) |
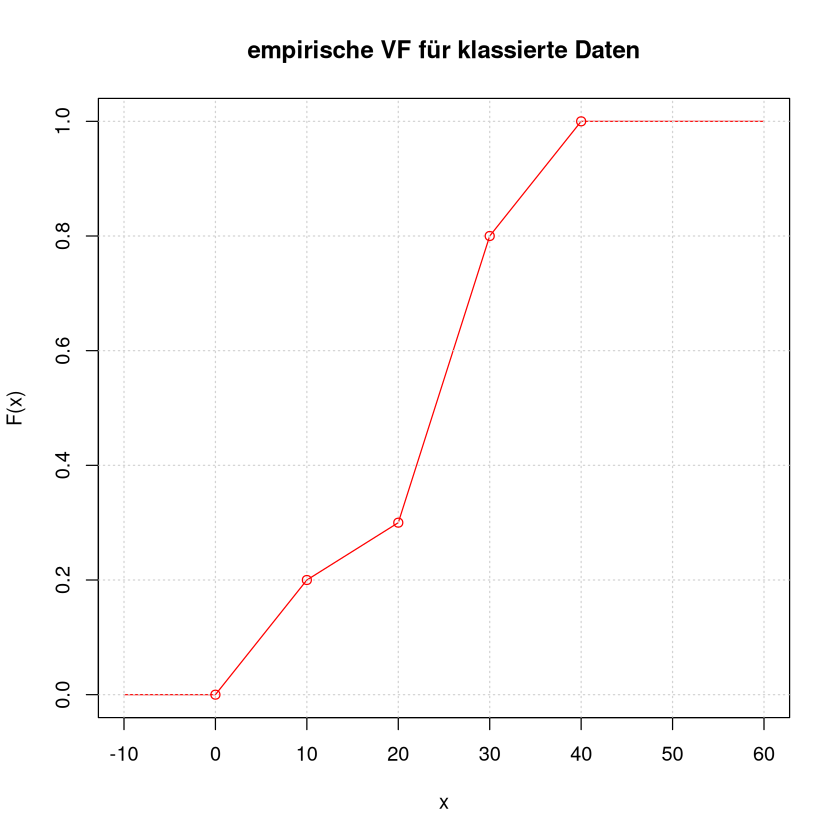
Die Tabelle sagt uns, dass 20 Werte im Intervall \((0,10]\) liegen, doch leider nicht wo genau sie sind. Anders ausgedrückt wissen wir dass \(1/5\) der Stichprobenwerte kleiner oder gleich 10 sind.
Erinnern wir uns an die empirische Verteilungsfunktion: der Wert an der Stelle \(x\) gibt den Anteil der Werte an, die kleiner oder gleich \(x\) sind. Daher wissen wir aus der (ersten Spalte der) Tabelle den richtigen Wert der Verteilungsfunktion an der Stelle \(x=10\), nämlich \(\frac15\). Aus der zweiten Spalten können wir den Wert an der Stelle 20 ablesen: \(\frac15+\frac1{10}=\frac{3}{10}\) usw.
Der genau Verlauf zwischen diesen bekannten Werten, ist aus der Tabelle nicht zu entnehmen. Daher wird die Funktion zwischen diesen Punkten linear verbunden.
x <- c(0,10 , 20 ,30 ,40)
y <- c(0,1/5, 3/10,8/10,1 )
plot(c(-10,x,60),c(0,y,1),type="l",col="red",xlab = "x",ylab = "F(x)",main="empirische VF für klassierte Daten")
grid()
points(x,y,col="red")
Merke
Liegen die Daten nur in klassierter Form vor, so erstelt man die empirische Verteilungsfunktion wie folgt:
Bilde zu jeder Klasse \((a_{i-1},a_i]\) die relativen Häufigkeiten \(f_i\).
Trage die Punkte \((a_i, f_i)\) im Koordinatensystem ab.
Trage den Punkt \((a_0, 0)\) im Koordinatensystem ab (wenn \((a_0,a_1]\) die erste Klasse ist).
Verbinde die Punkte durch gerade Linien.
Setze vom ersten Punkt nach links und den letzten Punkt nach rechts mit einer horizontalen Linie fort.