Binomialverteilung

Binomialverteilung#

Die Binomialverteilung beschreibt Wahrscheinlichkeiten für die Anzahl der Erfolge in einer festen Anzahl unabhängiger Bernoulli-Experimente mit gleicher Erfolgswahrscheinlichkeit.

Definition#

Definition

Es seien \(n\in\mathbb N\) und \(0\leq p\leq 1\) gegeben. Ist \(X\) eine Zufallsvariable, welche die Werte \(0,1,\dots,n\) annehmen kann und für die gilt

\[\mathbb{P}(X = k) = \binom{n}{k} p^k (1 - p)^{n-k}, \quad k = 0, 1, \dots, n,\]

so heißt \(X\) binomialverteilt mit Parameter \(n\) und \(p\). Wir schreiben dann

\[X \sim \mathrm{Bin}(n, p)\]

Anwendung#

Betrachtet man ein feste Anzahl von unabhängige Bernoulli-Experimenten und fragt sich „Wie oft habe ich Erfolg?“, so ist die Zufallsvariable, die diese Erfolge zählt Binomialverteilt. Zum Beispiel:

  • Würfeln: Anzahl der 6en beim 10maligen Würfeln ist \(\mathrm{Bin}(10,\frac16)\)-verteilt

  • Qualitätskontrolle: Wahrscheinlichkeit, dass genau 3 von 20 geprüften Glühbirnen defekt sind, bei einer Ausfallrate von 5 %.

  • Medizin: Wie wahrscheinlich ist es, dass 8 von 10 Patienten mit einem Medikament (70 % Erfolgsrate) genesen?

  • Sport: Ein Basketballspieler trifft 80 % seiner Freiwürfe. Wie hoch ist die Chance, dass er 5 von 6 Versuchen trifft?

  • Genetik: In einer Familie mit 5 Kindern (25 % Chance für ein bestimmtes Gen) – Wahrscheinlichkeit, dass genau 2 das Gen tragen.

  • Online-Marketing: Eine Anzeige hat eine Klickrate von 2 %. Wie wahrscheinlich sind mindestens 10 Klicks bei 500 Aufrufen?

Eigenschaften#

Erwartungswert:

\[\mathbb{E}(X) = n p\]

Varianz:

\[\mathrm{Var}(X) = n p (1 - p)\]

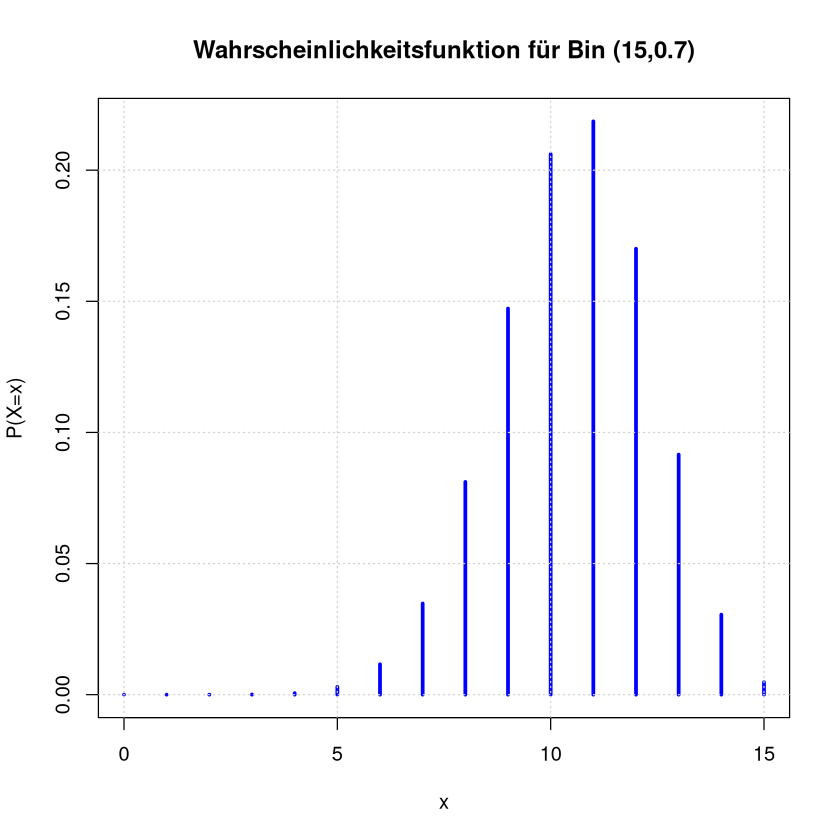
Stabdiagramm

Hide code cell source 
n     <- 15
p     <- 0.7
x     <- 0:n
probs <- dbinom(x,size = n, prob = p)

title <- paste("Wahrscheinlichkeitsfunktion für Bin (", n , "," , p , ")", sep="" )
plot(x = x, y = probs, col = "blue", type = "h", lwd = 3,
     main = title, ylab = "P(X=x)", xlab = "x")
grid()
../_images/484d9551e12d0aeac43a55a5c53bff96560b7e5abf66cefa91d5ebaad37c8879.png

Um ein besseres Gefühl für den Einfluss von \(n\) und \(p\) zu bekommen, können Sie

  • den R-Code anpassen oder

  • auf Geogebra damit experimentieren oder gleich hier:

 

 

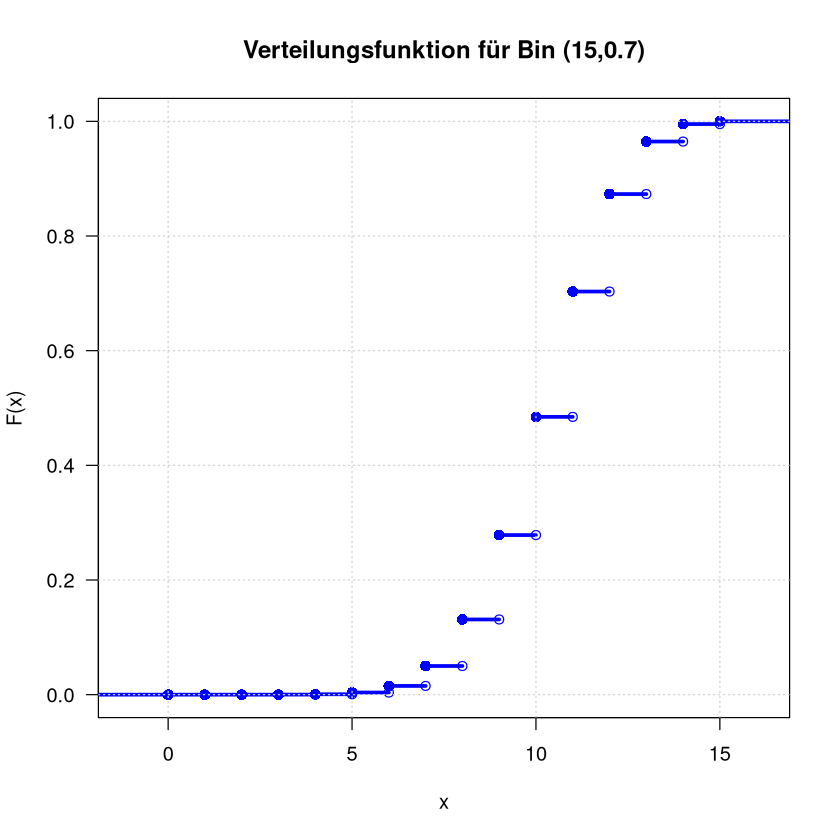
Verteilungsfunktion:

Hide code cell source 
plot.dcdf <- function(x, prob , col="blue", lwd=3, ...) {
  y   <- c(0,cumsum(prob))
  cdf <- stepfun(x=x, y=y, right=TRUE)
  plot(cdf, verticals=FALSE,
       lwd=lwd, col=col, las=1, 
       xlab="x", ylab="F(x)", ...)
  points(x,cumsum(prob),pch = 16, col=col, cex=1.2)
}
title <- paste("Verteilungsfunktion für Bin (", n , "," , p , ")", sep="" )
plot.dcdf(x, probs, main=title)
grid()
../_images/8a787bd586ec5a298a7aec2300f202d67ba0243e4e2815571ae7e78c4bd3b3b0.png

Beispiel#

Beispiel: Genetik

In einer bestimmten Familie hat jedes der 5 Kinder die Wahrscheinlicheit \(0.25\) eine bestimmte Genkombination von Ihren Eltern vererbt zu bekommen. Die Genkombination erzeugt grüne Augen. Alle anderen Genkombintionen die hier entstehen können erzeugen braune Augen.

  1. Wie groß ist die Wahrscheinlichkeit, dass genau 2 der Kinder grüne Augen haben?

  2. Wie groß ist die Wahrscheinlichkeit, dass mindestens 2 der Kinder grüne Augen haben?

  3. Wie viele Kinder haben in einer solchen Situation (Familie mit 5 Kindern und Wahrscheinlichkeit \(0.25\)) im Mittel grüne Augen.

Lösung

\(X\) … Anzahl der Kinder (unter 5) mit grünen Augen, es gilt laut Aufgabenstellung:

\[X\sim \mathrm{Bin}(5, 0.25)\]

  1. Gesucht: \(\mathbb P(X=2)\)

    \[\begin{align*}\mathbb P(X=2) = \binom{n}{2}p^2 (1-p)^{n-2} = \binom{5}{2}\cdot 0.25^2 \cdot 0.75^{3} = 0.263671875 \end{align*}\]

    R-Befehl:

    dbinom(2,5,0.25)
# oder
dbinom(2 ,size=5, prob=0.25 )

    Erklärung: dbinom(2,5,0.25) liefert den Wert der Wahrscheinlichkeitsfunktion der Binomialverteilung an der Stelle \(2\) für die Parameter \(n=5\) und \(p=0.25\), also \(\mathbb P(X=2)\) für \(X\sim\mathrm{Bin}(5,0.25)\)

  2. Gesucht: \(\mathbb P(X\geq 2)\)

    \[\begin{split}\begin{align*}\mathbb P(X\geq 2) &= 1- \mathbb P(X < 2) \\ &= 1- \mathbb P(X \leq 1) \\ &= 1- F_X(1) \\ &= 1- (\mathbb P(X = 0)+\mathbb P(X = 1)) \\ &= 1- \left(\binom{5}{0}\cdot 0.25^0 \cdot 0.75^{5}+\binom{5}{1}\cdot 0.25^1 \cdot 0.75^{4}\right) \\ &= 1- (0.2373 + 0.3956) = 0.3671 \end{align*}\end{split}\]
    1 - (dbinom(0,5,0.25) + dbinom(1,5,0.25))
# oder
1 - (pbinom(1 ,size=5, prob=0.25 ))

    Erklärung: pbinom(1,5,0.25) liefert den Wert der Verteilungsfunktion der Binomialverteilung an der Stelle \(1\) für die Parameter \(n=5\) und \(p=0.25\), also \(\mathbb P(X\leq 1)\) für \(X\sim\mathrm{Bin}(5,0.25)\)

  3. Gesucht: \(\mathbb E(X)\)

    \[\mathbb E(X) = n \cdot p = 5 \cdot 0.25 = 1.25 \]

    Eine Familie mit dieser Genkonstellation und 5 Kindern hat im Mittel 1.25 Kinder mit grünen Augen.

Beziehung zur Bernoulli Verteilung#

Aus vielen Bernoullis wird Binomial…#

Wir haben schon gelernt: führt man \(n\) unabhängige identische Bernoulli-Experimente durch und fragt nach der Anzahl der Erfolge, so ist diese Binomialverteilt. Etwas formaler ausgedrückt: Sind \(X_1,\dots, X_n\) unabhängige mit Parameter \(p\) Bernoulli-verteilte Zufallsvariablen, so gilt ist die Summe \(X_1+\dots+X_n\) Binomialverteilt mit Parameter \(n\) und \(p\), also

\[X_1+\dots+X_n \sim \mathrm{Bin}(n,p)\]

Bernoulli ist eine spezielle Binomalverteilung#

Wählen wir in obiger Überlegung \(n=1\). Dann zählen wir nur die Erfolge von einem Bernoulli-Experiment. Die Anzahl der Erfolge ist also genau das Ergebnis des Bernoulli-Experiments (\(0\) oder \(1\)). Also eine Zufallsvariable \(X\sim \mathrm{Bin}(1,p)\) immer eine mit Parameter \(p\) Bernoulli-verteilte Zufallsvariable.

Merke

Die Bernoulli-Verteilung ist ein Spezialfall der Binomialverteilung (mit \(n=1\)).

Umsetzung in R#

Es sei \(X\sim \mathrm{Bin}(n,p)\).

  • Die Werte der Wahrscheinlichkeitsfunktion bekommt man mit dbinom

  • Die Werte der Verteilungsfunktion bekommt man mit pbinom

  • Will man zufällige Werte erzeugen, welche gemäß der Verteilung gezogen wurden , nutzt man rbinom

Es sei \(X\sim \mathrm{Bin}(25,0.3)\). Gesucht ist \(\mathbb P(X=7)\) und \(\mathbb P(X\leq 8)\)

# Um die WK von  X=7  zu berechnen nutzen wir   dbinom(...)
# Das 1. Argument ist die Stelle von der wir die WK wissen wollen
# das 2. Argument ist n, das 3. ist p
dbinom(7, size = 25, prob = 0.3)

# Um die WK von  X <= 8  zu berechnen nutzen wir   pbinom(...)
# Das 1. Argument ist die Stelle von der wir die VF auswerten wollen
# das 2. Argument ist n, das 3. ist p
pbinom(8, size = 25, prob = 0.3)
0.171193639691951
0.676928125102868

Will man andere Wahrscheinlichkeiten bestimmen, schreibt man diese um in Ausdrücke die \(\mathbb P(X=a)\) oder \(\mathbb P(X\leq b)\) enthalten, z.B.

\[\mathbb P(4\leq X\leq 6)= \mathbb P(X=4) + \mathbb P(X=5) + \mathbb P(X=6)\]

oder

\[\mathbb P(4\leq X\leq 6)= \mathbb P(X\leq 6) - \mathbb P(X\leq 3)\]
# Um die WK von (4<= X <= 6) zu berechnen nutzen wir dbinom
dbinom(4, 25, 0.3) + dbinom(5, 25, 0.3) + dbinom(6, 25, 0.3)

# oder  pbinom
pbinom(6, size = 25, prob = 0.3) - pbinom(3, size = 25, prob = 0.3)
0.307414387688549
0.307414387688549

Wollen wir entsprechend der Verteilung \(\mathrm{Bin}(25,0.7)\) zufällige Zahlen erzeugen, gehen wir wie folgt vor:

# erzeugt 10 Zufallszahlen aus der Verteilung Bin(25,0.7)
rbinom(10, 25, 0.3)
  1. 11
  2. 10
  3. 5
  4. 10
  5. 10
  6. 7
  7. 9
  8. 9
  9. 9
  10. 2

Sollen 20 Bernoulli-verteilte Zufallsvariablen mit p=0.3 erzeugt werden, setzen wir \(n\) auf \(1\):

# erzeugt 20 Zufallszahlen aus der Verteilung Ber(0.3)
set.seed(439)       # Setzt den Startpunkt für die Erzeugung der Pseudozufallszahlen 
                    # Zahl kann beliebig gewählt werden. 
                    # Sorgt dafür, dass der "Zufall" immer die gleichen Ergebnisse liefert.
rbinom(20, 1 , 0.3)
  1. 1
  2. 1
  3. 1
  4. 0
  5. 0
  6. 1
  7. 1
  8. 0
  9. 1
  10. 1
  11. 0
  12. 0
  13. 0
  14. 0
  15. 0
  16. 0
  17. 1
  18. 0
  19. 0
  20. 0