Lineare Regression in R

Hier wollen wir nun besprechen wie eine lineare Regression in R durgeführt wird.

Grundlegende Syntax

In R lässt sich eine lineare Regression sehr einfach mit der Funktion lm() (linear model) durchführen. Die Syntax lautet:

lm( y ~ x )

wenn in x und y die Daten abgespeichert sind. Der Ausdruck y~x ist eine Formel und sagt, dass wir y durch x erklären wollen.

Haben wir einen Datensatz vorliegen in Form eines data.frame, so kann man zusätzlich den Datensatz angeben und muss dann in der Formel nur die Spaltennamen erwähnen.

Haben wir etwa den data.frame names koerper mit den 2 Spalten gewicht und groesse. Dann

koerper <- data.frame(gewicht=c(74,68,93,83,80),groesse=c(175,172,185,176,179))
koerper

# Regressiongerade berechnen
lm(gewicht ~ groesse, data = koerper)

A data.frame: 5 × 2

gewicht	groesse
<dbl>	<dbl>
74	175
68	172
93	185
83	176
80	179

Call:
lm(formula = gewicht ~ groesse, data = koerper)

Coefficients:
(Intercept)      groesse  
   -237.603        1.788  

Alternativ kann man auch

lm(koerper$gewicht ~ koerper$groesse)

eingeben. Dann ist aber die Ausgabe etwas unübersichtlicher.

Schauen wir uns die Ausagbe an:

• Call: hier steht noch einmal die Eingabe, damti man sieht welches Modell gerechnet wurde

• Coefficients: Unter (Intercept) steht der Achsenabschnitt auf der \(y\)-Achse; unter groesse steht der Anstieg, der Faktor vor x

Beispiel

Die Daten und das Modell

Anhand eines in R integrierten Datensatzs wollen wir die lineare Regression üben. Der Datensatz mtcars enthält Daten über verschieden Fahrzeuge. Zunächst verschaffen wir uns einen Überblick:

dim(mtcars)
head(mtcars)

1. 32
2. 11

A data.frame: 6 × 11

	mpg	cyl	disp	hp	drat	wt	qsec	vs	am	gear	carb
	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
Mazda RX4	21.0	6	160	110	3.90	2.620	16.46	0	1	4	4
Mazda RX4 Wag	21.0	6	160	110	3.90	2.875	17.02	0	1	4	4
Datsun 710	22.8	4	108	93	3.85	2.320	18.61	1	1	4	1
Hornet 4 Drive	21.4	6	258	110	3.08	3.215	19.44	1	0	3	1
Hornet Sportabout	18.7	8	360	175	3.15	3.440	17.02	0	0	3	2
Valiant	18.1	6	225	105	2.76	3.460	20.22	1	0	3	1

Der Datensatz hat also 32 Zeilen (Fahrzeuge) und 11 Spalten (erhobene Merkmale der Fahrzeuge). Um mehr über den Datensatz zu erfahren, nutzen Sie die Eingabe help(mtcars).

Wir wollen nun die beiden Spalten mpg (Meilen pro Gallone) und wt (Gewicht) auf einen linearen Zusammenhang hin untersuchen.

mod <- lm(mpg~wt, data=mtcars)
mod

Call:
lm(formula = mpg ~ wt, data = mtcars)

Coefficients:
(Intercept)           wt  
     37.285       -5.344  

Die Regressiongerade ist also \(y=37.285 -5.344x\), wenn \(y\) der mpg-Wert und \(x\) das Gewicht ist.

Visualisierung

Wir wollen diese Gerade zummen mit den den Daten plotten.

# Plot-Befehl der Punkte
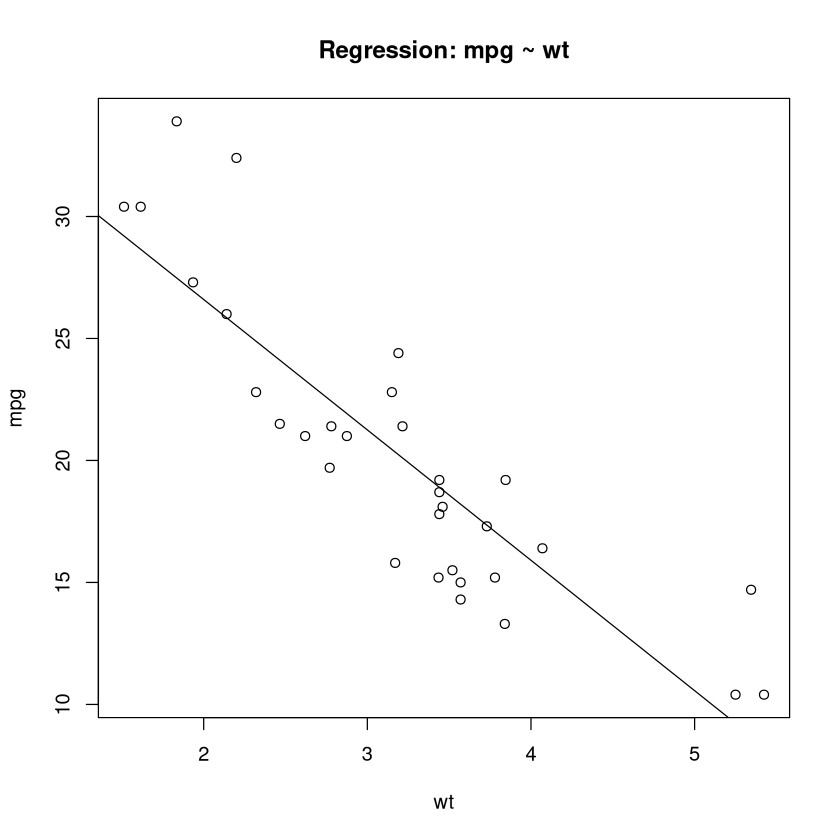
plot(mpg~wt, data=mtcars, main = "Regression: mpg ~ wt")
# Plot-Befehl für die Regressionsgerade
abline(mod)

Wir erkennen, dass mit zunehmenden Gewicht die Reichweite mit einer Gallone immer geringer wird. Der Koeffizient vor wt ist \(-5.344\), dies ist der Anstieg der Geraden. Er sagt, dass falls ein Auto 1000 lbs mehr wiegt als ein anderers, es durchschnittlich mit einer Gallone \(5.344\) Meilen weniger weit fahren kann.

Bestimmtheitsmaß

Wir berechnen \(R^2\) über das Quadrat des Korrelationskoeffizienten.

cor(mtcars$mpg,mtcars$wt)^2

0.752832793658264

Prädiktion

Wir fragen uns nun welchen mpg wir erwarten würden, wenn wir ein „neues“ Auto mit einem Gewicht von \(4500\) lbs betachten. Dazu muss man nur den Wert \(4.500\) in die Gleichung eingesetzt werden:

\[37.285 -5.344 \cdot 4.5 = 13.237 \]

Wir müssten also damit rechnen, dass wir mit diesem Fahrzeug mit einer Gallone 13.237 Meilen fahren können.

In R können wir dazu auch den Befehl predict() nutzen. Als newdata wird ein data.frame verlangt. Dieser hat nur eine Spalte (wt) und in der Spalte steht nur der eine Wert \(4.5\).

predict(mod,newdata = data.frame(wt=4.5))

1: 13.23500409009