Kolmogorov-Smirnov-Test

Kolmogorov-Smirnov-Test#

… ein parameterfreier Test zum Prüfen ob eine Stichporbe zu einer gegebenen Verteilung passt.

Bei der Durchführung des Tests halten wir uns and die bekannte Vorgehenweise. Im Folgenden werden die zugehörigen konkreten Hypothesen, Testgrößen, kritischen Bereiche und p-Werte besprochen.

Grundlagen#

Aufgabenstellung:
Anhand einer Stichprobe soll geprüft werden, ob die Verteilungsfunktion \(F\) eines Merkmals \(X\) gleich einer vollständig bekannten stetigen Verteilungsfunktion \(F_0\) ist.

Nullhypothese: \(F_0\) ist die wahre Verteilungsfunktion

Idee:
Vergleiche Verteilungsfunktion \(F_0\) mit empirischer Verteilungsfunktion \(S_n\) der Stichprobe

  • Funktionen ähnlich \(\rightsquigarrow\) spricht für \(H_0\)

  • Funktionen sehr unterschiedlich \(\rightsquigarrow\) spricht gegen \(H_0\)

Was heißt Funktionen ähnlich?

maximaler Abstand der Funktionswerte klein!

Hide code cell source 
# Beispiel-Stichprobe 
set.seed(42)
x <- rnorm(30, mean = 0, sd = 1.0)  # N(0,1) Daten

# Sortierte Stichprobe
x_sorted <- sort(x)

# Empirische Verteilungsfunktion
edf <- ecdf(x)

# x-Werte für die Darstellung
x_vals <- seq(min(x) - 1, max(x) + 1, length.out = 1000)

# Theoretische Verteilungsfunktion (Standardnormalverteilung)
F_theo <- pnorm(x_vals)

# Plot
plot(x_vals, F_theo, type = "l", lwd = 2, col = "blue",
     xlab = "x", ylab = "F(x)",
     main = "Empirische vs. Standardnormal-Verteilungsfunktion")

# Empirische Verteilungsfunktion hinzufügen
lines(edf, verticals = FALSE, do.points = T, col = "darkgreen", lwd = 2, cex=0.8)

# Berechnung des maximalen Abstands (KS-Statistik)
edf_vals <- edf(x_sorted)
pnorm_vals <- pnorm(x_sorted)
ks_diff <- abs(edf_vals - pnorm_vals)
D <- max(ks_diff)
i_max <- which.max(ks_diff)
x_max <- x_sorted[i_max]

# Markierung des maximalen Abstands
segments(x0 = x_max, y0 = pnorm_vals[i_max], y1 = edf_vals[i_max],
         col = "red", lwd = 2, lty = 2)

# Beschriftung D
text(x_max, (pnorm_vals[i_max] + edf_vals[i_max]) / 2,
     labels = paste0("D = ", round(D, 3)),
     pos = 4, col = "red", cex = 0.9)

# Legende
legend("bottomright",
       legend = c("Standardnormalverteilung", "Empirische Verteilungsfunktion", "Max. Abstand D"),
       col = c("blue", "darkgreen", "red"),
       lty = c(1, 1, 2),
       lwd = c(2, 2, 2))
../_images/e18faa3e90d77e1016781a0e3278557272ee5472c816c5f9a385124195516947.png

Gegeben/Vorbereitung:

  • Mathematische Stichprobe \(X_1, \dots, X_n\)

  • Konkrete Stichprobe \(x_1, \dots, x_n\) mit Ausprägungen

    \[ a_1 < a_2 < \dots < a_k \quad (k \leq n) \]

    und Häufigkeiten \(h_1, \dots, h_k\)

  • Relative Summenhäufigkeiten:

    \[ s_0 := 0 \quad \text{und} \quad s_j := \frac{1}{n} \sum_{i=1}^j h_j \]

  • Hilfsgrößen:

    \[\begin{split}\begin{align*} D_1 &= \max_{j=1,\dots,k} (F_0(a_j) - s_{j-1}),\\ D_2 &= \max_{j=1,\dots,k} (s_j - F_0(a_j)) \end{align*}\end{split}\]

  • Es gilt: Maximaler Abstand zwischen den Funktionen ist

    \[ \sup_{x \in \mathbb{R}} |S_n(x) - F_0(x)| = \max(D_1, D_2) \]

Vorgehen#

  1. Signifikanzniveau \(\alpha\) wählen

  2. Hypothesen:

    \[ H_0: F = F_0 \quad \text{und} \quad H_1: F \neq F_0 \]

  3. Testgröße:

    \[ T = \sup_{x \in \mathbb{R}} |S_n(x) - F_0(x)| \]

    \(S_n\) … empirische Verteilungsfunktion zur Stichprobe \(X_1,\dots,X_n\).
    \(T\) ist Kolmogorov-Smirnov-verteilt mit Parameter \(n\).

    Konkreter Testwert:

    \[ \boxed{t = T(\mathbf{x}) = \max(D_1, D_2)} \]

  4. Kritischer Bereich:

    \[ (K_{n, 1-\alpha},\, 1] \]

    \(K_{n, 1-\alpha}\) … \((1-\alpha)\)-Quantil der Kolmogorov-Smirnov-Verteilung mit Parameter \(n\)
    (zu entnehmen aus Tabellen oder Software)

    In R berechnet man \(K_{n,1-\alpha}\) unter Verwendung der Funktion critical.value.ks.test aus dem Paket BoutrosLab.plotting.general:

    library("BoutrosLab.plotting.general")
critical.value.ks.test(n, 1-alpha)

  5. Testentscheidung:

    • \(t \in K \quad \Rightarrow \quad H_0\) ablehnen, d.h.
      wir verwerfen die Hypothese, dass \(X\) entsprechend der Verteilungsfunktion \(F_0\) verteilt ist.

    • \(t \notin K \quad \Rightarrow \quad H_0\) nicht ablehnen, d.h.
      auf Grundlage der Stichprobe \(x_1,\dots, x_n\) lässt sich zum vorgegebenen Signifikanzniveau nichts gegen die Nullhypothese einwenden.

Bemerkungen#

  • Der Kolmogorov-Smirnov-Test ist auch für kleine Stichprobenumfänge verwendbar. Es entsteht kein Informationsverlust durch Klassenbildung.

  • Der Kolmogorov-Smirnov-Test ist prinzipiell auch im diskreten Fall anwendbar. Hier ist er aber sehr konservativ, d.h. es wird länger als notwendig an der Nullhypothese festgehalten (der kritische Bereich ist zu klein, der Test ist zu unkritisch gegenüber \(H_0\)).

  • Es gibt Versionen des Kolmogorov-Smirnov-Tests für Verteilungsfunktionen \(F_0\) mit geschätzten Parametern. Beispielsweise ist der Lilliefors Test ein Test auf Normalverteilung mit unbekannten Parametern \(\mu\) und \(\sigma\).

Beispiel#

Eine Stichprobe vom Umfang \(n=10\) ergab die Werte

\[ 2.04,\, 0.75,\, 0.46,\, -2.81,\, 2.04,\, 0.46,\, -1.63,\, 0.82,\, 1.72,\, 2.66 \]

Man überprüfe (zum Signifikanzniveau \(0.05\)), ob die Werte aus einer \(\mathrm{N}(0,1)\)-Verteilung stammen können.

Lösung: Kolmogorov-Smirnov-Test

  1. Signifikanzniveau: \(\alpha = 0.05\)

  2. Hypothesen:

    \[ H_0: F = \Phi, \quad H_1: F \neq \Phi \]

    wobei \(\Phi\) die Verteilungsfunktion der Standardnormalverteilung und \(F\) die wahre Verteilung des Merkmals ist.

  3. Testgröße:

    \[ T = \sup_{x \in \mathbb{R}} |S_n(x) - \Phi(x)| \]

    wobei \(S_n\) die empirische Verteilungsfunktion der Stichprobe (der Größe \(n\)) ist.

    konkreter Testwert:

    \[ t = \max(D_1, D_2) \]

    Bestimmen von \(D_1\) und \(D_2\) mittels Tabelle:

    \(j\)

    \(a_j\)

    \(h_j\)

    \(s_j = \frac{1}{n} \sum_{i=1}^j h_i\)

    \(F_0(a_j) = \Phi(a_j)\)

    \(F_0(a_j) - s_{j-1}\)

    \(s_j - F_0(a_j)\)

    1

    -2.81

    1

    0.1

    0.0025

    0.0025

    0.0975

    2

    -1.63

    1

    0.2

    0.0516

    < 0

    0.1484

    3

    0.46

    2

    0.4

    0.6772

    0.4772

    < 0

    4

    0.75

    1

    0.5

    0.7734

    0.3734

    < 0

    5

    0.82

    1

    0.6

    0.7939

    0.2939

    < 0

    6

    1.72

    1

    0.7

    0.9573

    0.3573

    < 0

    7

    2.04

    2

    0.9

    0.9793

    0.2793

    < 0

    8

    2.66

    1

    1.0

    0.9961

    0.0961

    0.0039

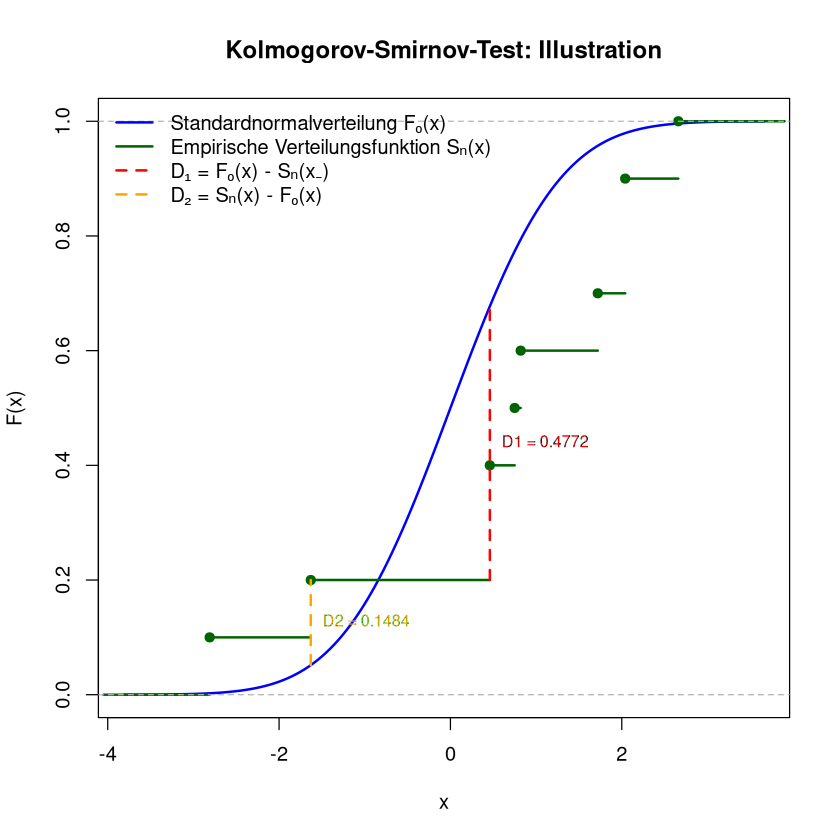
    Beachte: Wir schreiben hier \(s_j\) für die konkrete empirische Verteilungsfunktion an der Stelle \(a_j\) ausgewertet, d.h. \(s_j := s_n(a_j)\).

    \[ D_1 = 0.4772, \quad D_2 = 0.1484 \quad \Rightarrow \quad \boxed{t = 0.4772} \]

  4. Kritischer Bereich:

    \[ K = (K_{10,0.95}, 1] = (0.4092, 1] \]

    mit R:

    library("BoutrosLab.plotting.general")
critical.value.ks.test(10,0.95)

  5. Entscheidung:

    \[ t \in K \quad \Rightarrow \quad H_0 \text{ wird abgelehnt.} \]

  6. Interpretation:
    Auf Grundlage der Stichprobe verwerfen wir (bei Signifikanzniveau 0.05) die Hypothese, dass die Daten von einem standardnormalverteilten Merkmal stammen.

Hide code cell source 
# Stichprobe
x <- c(2.04, 0.75, 0.46, -2.81, 2.04, 0.46, -1.63, 0.82, 1.72, 2.66)

# Sortierte Stichprobe
x_sorted <- sort(x)
n <- length(x)

# Empirische Verteilungsfunktion
edf <- ecdf(x)

# Standardnormalverteilung
x_vals <- seq(min(x) - 1, max(x) + 1, length.out = 1000)
F_theo <- pnorm(x_vals)

# Plot Grundstruktur
plot(x_vals, F_theo, type = "l", lwd = 2, col = "blue",
     xlab = "x", ylab = "F(x)", main = "Kolmogorov-Smirnov-Test: Illustration")

# Empirische Verteilungsfunktion zeichnen
lines(edf, verticals = FALSE, do.points = TRUE, col = "darkgreen", lwd = 2)

# EDF-Werte bei den Sprungstellen
edf_vals <- sapply(x_sorted, edf)
edf_vals_shifted <- c(0, edf_vals[-n])

# Standardnormalverteilung an den Stellen a_j
pnorm_vals <- pnorm(x_sorted)

# D1 = max(F0(a_j) - S_n(a_{j-1}))
d1_vec <- pnorm_vals - edf_vals_shifted
D1 <- max(d1_vec)
i_d1 <- which.max(d1_vec)

# D2 = max(S_n(a_j) - F0(a_j))
d2_vec <- edf_vals - pnorm_vals
D2 <- max(d2_vec)
i_d2 <- which.max(d2_vec)

# Markierung D1
segments(x0 = x_sorted[i_d1], x1 = x_sorted[i_d1],
         y0 = edf_vals_shifted[i_d1], y1 = pnorm_vals[i_d1],
         col = "red", lwd = 2, lty = 2)
text(x_sorted[i_d1], (pnorm_vals[i_d1] + edf_vals_shifted[i_d1]) / 2,
     labels = paste0("D1 = ", round(D1, 4)), pos = 4, col = "red", cex = 0.8)

# Markierung D2
segments(x0 = x_sorted[i_d2], x1 = x_sorted[i_d2],
         y0 = pnorm_vals[i_d2], y1 = edf_vals[i_d2],
         col = "orange", lwd = 2, lty = 2)
text(x_sorted[i_d2], (pnorm_vals[i_d2] + edf_vals[i_d2]) / 2,
     labels = paste0("D2 = ", round(D2, 4)), pos = 4, col = "orange", cex = 0.8)

# Legende
legend("topleft",
       legend = c("Standardnormalverteilung F₀(x)",
                  "Empirische Verteilungsfunktion Sₙ(x)",
                  "D₁ = F₀(x) - Sₙ(x₋)",
                  "D₂ = Sₙ(x) - F₀(x)"),
       col = c("blue", "darkgreen", "red", "orange"),
       lty = c(1, 1, 2, 2),
       lwd = 2,
       bty = "n")
../_images/a17b07e4eb5b51c01c2a80b1643ab9647e0dfdb838a690ac406109b4a61da031.png

Umsetzung des Kolmogorov-Smirnov-Tests in R#

In R kann der Kolmogorov-Smirnov-Test mit der Funktion ks.test() durchgeführt werden.

Beispiel: Test auf Standardnormalverteilung#

Gegeben ist eine Stichprobe:

x <- c(2.04, 0.75, 0.46, -2.81, 2.04, 0.46, -1.63, 0.82, 1.72, 2.66)
ks.test(x, "pnorm", mean = 0, sd = 1)

Beispielausgabe:

One-sample Kolmogorov-Smirnov test

data:  x
D = 0.48, p-value = 0.04056
alternative hypothesis: two-sided

Interpretation:

  • Teststatistik \(D = 0.48\)

  • p-Wert \(\approx 0.041\)

  • Bei einem Signifikanzniveau von \(\alpha=0.05\) wird \(H_0\) abgelehnt, da \(p<\alpha\). Wir gehen also davon aus, dass die Daten nicht aus einer Standardnormalverteilung stammen.

Andere Verteilungen:

Will man nicht auf die Normalverteilung testen, so ersetzt man das zweite Argument im Befehl ks.test() durch die passende Verteilungsfunktion. Dahinter gibt man den bzw die Parameter der Verteilung ein. Beispiel:

ks.test(x, "pexp", 4)

Hier wird die Nullhypothese „Daten stammen aus der Exponentialverteilung mit \(lambda=4\)“ getestet.

Weiteres zum KS-Test#

Zwei Stichproben-Test#

In einer leicht abgewandelten Variante kann man mit dem Kolmogorov-Smirnov-Test prüfen, ob zwei Stichproben der selben Verteilung entstammen können. Dabei werden beide empirischen Verteilungsfunktionen miteinander verglichen. Als Testgröße dient der maximale Abstand zwischen den Funktionen. In R wird dies ebenfalls mit der Funktion ks.test umgesetzt.

Beispiel:

x1 <- rnorm(50, mean = 0)
x2 <- rnorm(50, mean = 1)
ks.test(x1, x2)

	Exact two-sample Kolmogorov-Smirnov test

data:  x1 and x2
D = 0.42, p-value = 0.000246
alternative hypothesis: two-sided

Hier testet man die Hypothese:

  • \(H_0\): Beide Stichproben stammen aus derselben Verteilung

  • \(H_1\): Die Verteilungen unterscheiden sich

Alternative: Lilliefors-Test#

Neben dem Kolmogorov-Smirnov Test gibt es noch den Lilliefors-Test dieser unterscheidet sich in hauptsächlich in den folgenden 2 Punkten vom hier vorgestellten Kolmogorov-Smirnov-Test:

  • er ist ausschließlich geeignet um eine Stichprobe auf Normalverteilung zu testen

  • er benötigt keine vorgegebenen Paramerter, stattdessen werden \(\mu\) und \(\sigma\) innerhalb des Tests geschätzt

In R setzt mnd den Lillifors-Test mit lillie.test aus dem Paket nortest um:

install.packages("nortest")
library(nortest)
lillie.test(x)