Zwei nominale Merkmale#
Werden 2 Merkmale abgefragt, so sieht eine Stichprobe der Größe \(n\) folgendermaßen aus:
Der erste Eintrag gehört jeweils zum Merkmal \(X\), der zweite zum Merkmal \(Y\).
In diesem Kapitel sollen die beteiligten Merkmale beide nominal messbar sein. Wir stellen uns zum Beispiel Augenfarbe und Haarfarbe vor.
Kontingenztafeln#
Die Daten einer solchen Stichprobe lassen sich dann in einer Tabelle, einer sogenannten Kontingenztafel abtragen. Diese wird folgendermaßen erstellt:
Definition
Sei \((x_1,y_1),\dots, (x_n,y_n)\) ein (zweidimensionale) Stichprobe für die Merkmale \(X\) und \(Y\). Die möglichen Ausprägungen von \(X\) sind \(a_1,\dots,a_k\) und die von \(Y\) sind \(b_1,\dots,b_m\). Mit \(h_{ij}\) bezeichnen wir die absolute Häufigkeit des Auftretens der Kombination \((a_i,b_j)\) in der Stichprobe. Die Kontingenztafel (auch Kontingenztabelle, Kreuztabelle) für die absoluten Häufigkeiten ist dann
\(b_1\) |
\(b_2\) |
\(\dots\) |
\(b_m\) |
Gesamt |
|
|---|---|---|---|---|---|
\(a_1\) |
\(h_{11}\) |
\(h_{12}\) |
\(\dots\) |
\(h_{1m}\) |
\(h_{1\cdot}\) |
\(a_2\) |
\(h_{21}\) |
\(h_{22}\) |
\(\dots\) |
\(h_{2m}\) |
\(h_{2\cdot}\) |
\(\vdots\) |
\(\vdots\) |
\(\vdots\) |
\(\ddots\) |
\(\vdots\) |
\(\vdots\) |
\(a_k\) |
\(h_{k1}\) |
\(h_{k2}\) |
\(\dots\) |
\(h_{km}\) |
\(h_{k\cdot}\) |
Gesamt |
\(h_{\cdot1}\) |
\(h_{\cdot 2}\) |
\(\dots\) |
\(h_{\cdot m}\) |
\(N\) |
Dabei sind
die sogenannten Randhäufigkeiten.
Beispiel
Es wurden 100 Personen befragt, ob Sie verheiratet (ja/nein) sind und welche politisch Partei (A/B/C/D) Sie bei der letzten Wahl gewählt haben. Dies ergab
Zählt man durch ergibt sich beispielsweise, dass 12 mal die Kombination \((\text{ja},\text{A})\) in der Stichprobe vorkommt, also dass genau 12 der Personen verheiratet waren und die Partei A gewählt haben. Diese Häufigkeiten tragen wir in der Kontingenztafel ab:
\(\text{Partei A}\) |
\(\text{Partei B}\) |
\(\text{Partei C}\) |
\(\text{Partei D}\) |
\(\text{Gesamt}\) |
|
|---|---|---|---|---|---|
\(\text{verheiratet}\) |
\(12\) |
\(9\) |
\(7\) |
\(26\) |
\(54\) |
\(\text{nicht verheiratet}\) |
\(8\) |
\(17\) |
\(15\) |
\(6\) |
\(46\) |
\(\text{Gesamt}\) |
\(20\) |
\(26\) |
\(22\) |
\(32\) |
\(100\) |
Es gibt auch die Möglichkeit die relativen Häufigkeiten in der Tabelle einzutragen. Dann erhält man die Kontingenztafel für relative Häufigkeiten:
Definition
Sei \((x_1,y_1),\dots, (x_n,y_n)\) ein (zweidimensionale) Stichprobe für die Merkmale \(X\) und \(Y\). Die möglichen Ausprägungen von \(X\) sind \(a_1,\dots,a_k\) und die von \(Y\) sind \(b_1,\dots,b_m\). Mit \(h_{ij}\) bezeichnen wir die absolute Häufigkeit und mit \(f_{ij}=\frac{h_{ij}}{n}\) relative Häufigkeit des Auftretens der Kombination \((a_i,b_j)\) in der Stichprobe. Die Kontingenztafel für die relativen Häufigkeiten ist dann
\(b_1\) |
\(b_2\) |
\(\dots\) |
\(b_m\) |
Gesamt |
|
|---|---|---|---|---|---|
\(a_1\) |
\(f_{11}\) |
\(f_{12}\) |
\(\dots\) |
\(f_{1m}\) |
\(f_{1\cdot}\) |
\(a_2\) |
\(f_{21}\) |
\(f_{22}\) |
\(\dots\) |
\(f_{2m}\) |
\(f_{2\cdot}\) |
\(\vdots\) |
\(\vdots\) |
\(\vdots\) |
\(\ddots\) |
\(\vdots\) |
\(\vdots\) |
\(a_k\) |
\(f_{k1}\) |
\(f_{k2}\) |
\(\dots\) |
\(f_{km}\) |
\(f_{k\cdot}\) |
Gesamt |
\(f_{\cdot1}\) |
\(f_{\cdot 2}\) |
\(\dots\) |
\(f_{\cdot m}\) |
\(1\) |
Dabei sind
die sogenannten relativen Randhäufigkeiten.
Schauen wir und in unserem Beispiel an
Beispiel
Es wurden 100 Personen befragt, ob Sie verheiratet (ja/nein) sind und welche politisch Partei (A/B/C/D) Sie bei der letzten Wahl gewählt haben. Dies ergab die Kontingenztafel (der absoluten Häufigkeiten)
\(\text{Partei A}\) |
\(\text{Partei B}\) |
\(\text{Partei C}\) |
\(\text{Partei D}\) |
\(\text{Gesamt}\) |
|
|---|---|---|---|---|---|
\(\text{verheiratet}\) |
\(12\) |
\(9\) |
\(7\) |
\(26\) |
\(54\) |
\(\text{nicht verheiratet}\) |
\(8\) |
\(17\) |
\(15\) |
\(6\) |
\(46\) |
\(\text{Gesamt}\) |
\(20\) |
\(26\) |
\(22\) |
\(32\) |
\(100\) |
Teilen wir alle Werte durch \(n=100\) erhalten wir den Kontingenztafel der relativen Häufigkeiten.
\(\text{Partei A}\) |
\(\text{Partei B}\) |
\(\text{Partei C}\) |
\(\text{Partei D}\) |
\(\text{Gesamt}\) |
|
|---|---|---|---|---|---|
\(\text{verheiratet}\) |
\(0.12\) |
\(0.09\) |
\(0.07\) |
\(0.26\) |
\(0.54\) |
\(\text{nicht verheiratet}\) |
\(0.08\) |
\(0.17\) |
\(0.15\) |
\(0.06\) |
\(0.46\) |
\(\text{Gesamt}\) |
\(0.2\) |
\(0.26\) |
\(0.22\) |
\(0.32\) |
\(1\) |
Den Übergang von absoluten zu relativen Werten, mittels Teilen durch eine Gesamtzahl, nennt man auch normieren.
Um einen Zusammenhang zwischen den betrachteten Merkmalen zu erkennen, ist es oft sinnvoll die Werte der Tabelle nicht mit \(n\) zu normieren, sondern
jede Zeile mit Ihrer Zeilensumme zu normieren oder
jede Spalte mit Ihrer Spaltensumme zu normieren.
Die so ermittelten Werte nennt man dann bedingte relative Häufigkeiten:
Definition
Sei \((x_1,y_1),\dots, (x_n,y_n)\) ein (zweidimensionale) Stichprobe für die Merkmale \(X\) und \(Y\). Die möglichen Ausprägungen von \(X\) sind \(a_1,\dots,a_k\) und die von \(Y\) sind \(b_1,\dots,b_m\). Mit \(h_{ij}\) bezeichnen wir die absolute Häufigkeit. Die bedingten relativen Häufigkeiten für \(X\) gegeben \(Y=b_j\) sind dann
Die bedingten relativen Häufigkeiten für \(Y\) gegeben \(X=a_i\) sind dann
Schauen wir uns das wieder am Beispiel an.
Beispiel
Es wurden 100 Personen befragt, ob Sie verheiratet (ja/nein) sind und welche politisch Partei (A/B/C/D) Sie bei der letzten Wahl gewählt haben. Dies ergab die Kontingenztafel (der absoluten Häufigkeiten)
\(\text{Partei A}\) |
\(\text{Partei B}\) |
\(\text{Partei C}\) |
\(\text{Partei D}\) |
\(\text{Gesamt}\) |
|
|---|---|---|---|---|---|
\(\text{verheiratet}\) |
\(12\) |
\(9\) |
\(7\) |
\(26\) |
\(54\) |
\(\text{nicht verheiratet}\) |
\(8\) |
\(17\) |
\(15\) |
\(6\) |
\(46\) |
\(\text{Gesamt}\) |
\(20\) |
\(26\) |
\(22\) |
\(32\) |
\(100\) |
Teilen wir alle Zeilen durch die Zeilensumme erhalten wir die relativen Häufigkeiten für \(X\) gegeben \(Y\):
\(\text{Partei A}\) |
\(\text{Partei B}\) |
\(\text{Partei C}\) |
\(\text{Partei D}\) |
\(\text{Gesamt}\) |
|
|---|---|---|---|---|---|
\(\text{verheiratet}\) |
\(0.222\) |
\(0.167\) |
\(0.120\) |
\(0.481\) |
\(1\) |
\(\text{nicht verheiratet}\) |
\(0.174\) |
\(0.360\) |
\(0.3261\) |
\(0.130\) |
\(1\) |
So erkennt man beispielsweise, dass unter den Verheirateten ca \(48.1\%\) Partei D gewählt haben, während sich unter den nicht verheirateten Personen nur \(13\%\) für Partei D entschieden. Wir beziehen uns also bei den Prozentzahlen jeweils auf die Untergruppe der Verheirateten oder Nicht-Verheirateten. Wir rechnen die Prozentzahlen also aus unter der Bedingung, dass wir nur die Untergruppe betrachten. Daher nennt man diese Größen bedingte relative Häufigkeiten.
Andersrum kann man Kontingentafel der absoluten Häufigkeiten natürlich auch durch die Spaltensummen teilen. So erhalten wir
\(\text{Partei A}\) |
\(\text{Partei B}\) |
\(\text{Partei C}\) |
\(\text{Partei D}\) |
|
|---|---|---|---|---|
\(\text{verheiratet}\) |
\(0.6\) |
\(0.346\) |
\(0.318\) |
\(0.8125\) |
\(\text{nicht verheiratet}\) |
\(0.4\) |
\(0.654\) |
\(0.682\) |
\(0.1875\) |
\(\text{Gesamt}\) |
\(1\) |
\(1\) |
\(1\) |
\(1\) |
Hier erkennt man nun, dass unter den Wählern der Partei D mehr als \(81\%\) verheiratet sind. Die Bezugsgruppe sind also jeweils alle Wähler einer bestimmten Partei.
Umsetzung in R#
Wir nutzen dazu wieder den Befehl table(). Werden 2 gleichlange Vektoren als Argumente eingegeben, erstellt der Befehl eine Kontingenztafel.
var1 <- c("C", "C", "C", "B", "C", "B", "B",
"B", "C", "A", "B", "B", "A", "B", "C", "A", "C", "C", "A", "A",
"A", "A", "C", "B", "C", "B", "A", "B", "C", "B", "A", "C", "C",
"A", "C", "B", "A", "C", "A", "A", "B", "C", "C", "A", "C", "A",
"C", "B", "A", "B")
var2 <- c("X", "X", "Z", "X", "Y", "X",
"X", "Z", "X", "Y", "X", "Z", "X", "Z", "Y", "Z", "Y", "Y", "Z",
"Y", "Y", "Z", "Z", "X", "Y", "Y", "X", "Y", "X", "X", "Y", "Z",
"Z", "X", "Y", "X", "Y", "X", "Z", "Z", "Y", "Z", "X", "Y", "Y",
"Z", "Y", "X", "Z", "Z")
rbind(var1,var2)
kontingenztafel <- table(var1,var2)
cat("Kontingenztafel der absoluten Häufigkeiten:")
kontingenztafel
cat("\nKontingenztafel der relativen Häufigkeiten:")
prop.table(kontingenztafel)
cat("\nKontingenztafel der bedingten relativen Häufigkeiten (bedingt auf var1):")
prop.table(kontingenztafel, margin=1)
cat("\nKontingenztafel der bedingten relativen Häufigkeiten (bedingt auf var2):")
prop.table(kontingenztafel, margin=2)
| var1 | C | C | C | B | C | B | B | B | C | A | ⋯ | B | C | C | A | C | A | C | B | A | B |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| var2 | X | X | Z | X | Y | X | X | Z | X | Y | ⋯ | Y | Z | X | Y | Y | Z | Y | X | Z | Z |
Kontingenztafel der absoluten Häufigkeiten:
var2
var1 X Y Z
A 3 6 7
B 8 3 4
C 6 8 5
Kontingenztafel der relativen Häufigkeiten:
var2
var1 X Y Z
A 0.06 0.12 0.14
B 0.16 0.06 0.08
C 0.12 0.16 0.10
Kontingenztafel der bedingten relativen Häufigkeiten (bedingt auf var1):
var2
var1 X Y Z
A 0.1875000 0.3750000 0.4375000
B 0.5333333 0.2000000 0.2666667
C 0.3157895 0.4210526 0.2631579
Kontingenztafel der bedingten relativen Häufigkeiten (bedingt auf var2):
var2
var1 X Y Z
A 0.1764706 0.3529412 0.4375000
B 0.4705882 0.1764706 0.2500000
C 0.3529412 0.4705882 0.3125000
Graphische Veranschaulichung#
Säulendiagramme#
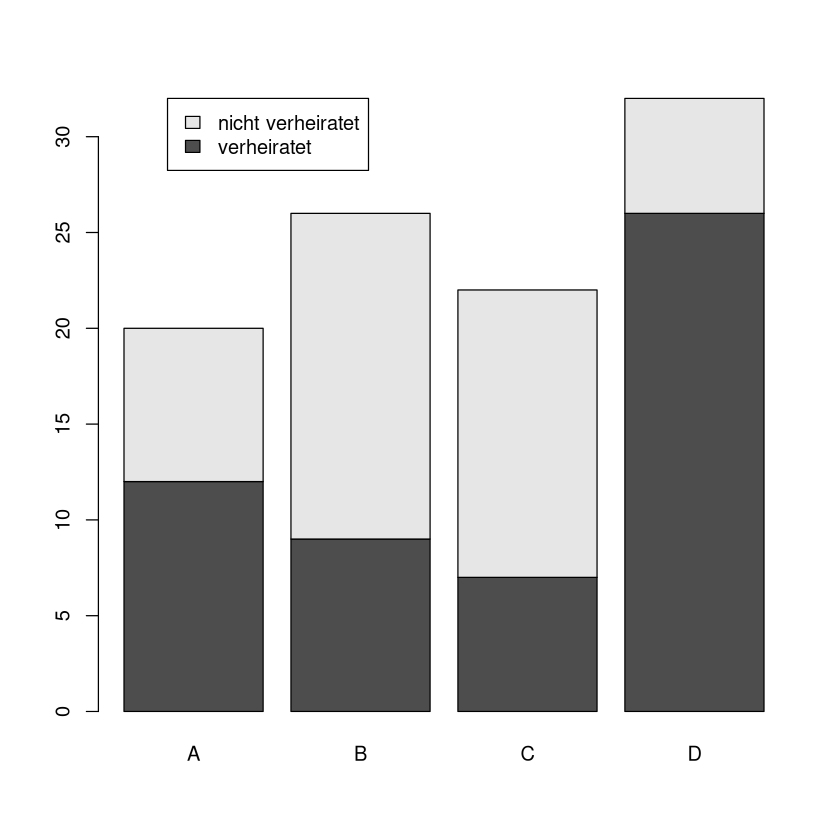
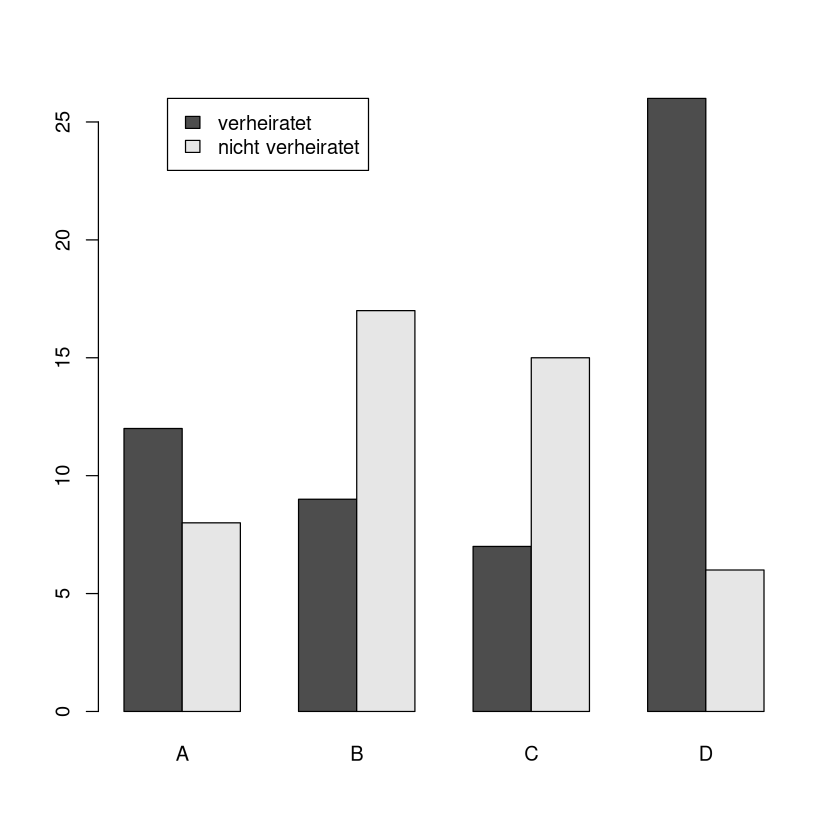
Hier bieten sich etwa gruppierte oder gestapelte Säulendiagramme an:
M <- matrix(c(12,9,7,26,8,17,15,6),byrow=T,nrow=2,dimnames = list(c("verheiratet","nicht verheiratet"),c("A","B","C","D")))
barplot(M,
legend.text = c("verheiratet","nicht verheiratet"),
args.legend = list(x = "topleft", # <- Legende steht links oben
inset = c(0.1,0)) # <- Legende wird noch leicht nach rechts verschoben
)
barplot(M,
beside=T,
legend.text = c("verheiratet","nicht verheiratet"),
args.legend = list(x = "topleft", # <- Legende steht links oben
inset = c(0.1,0)) # <- Legende wird noch leicht nach rechts verschoben
)
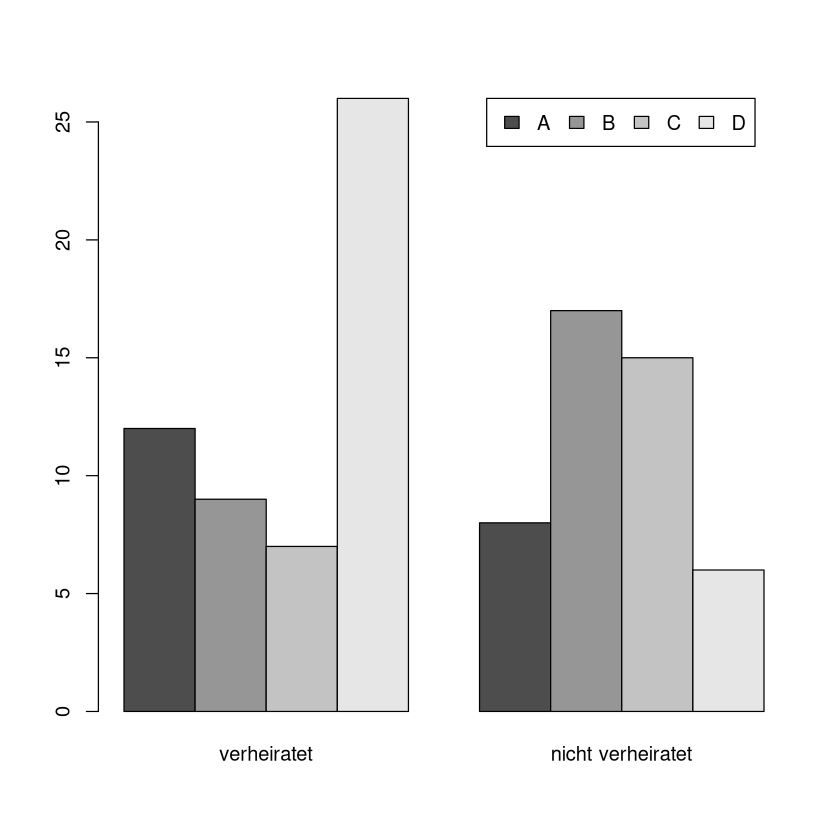
Wieder lassen sich die Diagramme auch andersrum gruppieren:
M <- matrix(c(12,9,7,26,8,17,15,6),byrow=T,nrow=2,dimnames = list(c("verheiratet","nicht verheiratet"),c("A","B","C","D")))
barplot(t(M),
legend.text = c("A","B","C","D"),
args.legend = list(x = "topright", # <- Legende steht links oben
inset = c(0.05,0), # <- Legende wird noch leicht nach rechts verschoben
horiz=T)
)
M <- matrix(c(12,9,7,26,8,17,15,6),byrow=T,nrow=2,dimnames = list(c("verheiratet","nicht verheiratet"),c("A","B","C","D")))
barplot(t(M),
beside=T,
legend.text = c("A","B","C","D"),
args.legend = list(x = "topright", # <- Legende steht links oben
inset = c(0.05,0), # <- Legende wird noch leicht nach rechts verschoben
horiz=T)
)
Mosaik-Diagramm#
Das Mosaik-Diagramm ist ähnlich wie das auf 100% skalierte gestapelte Säulendiagramm. Zusätzlich ist hier noch die Breite der Säule proportional zur relativen Häufigkeit der Gruppe. Auf diese Weise ist die Größe jeder einzelnen Fläche proportional zur relativen Häufigkeit.
Maßzahlen#
Der 2x2 Fall#
Hier betrachten wir den Fall, dass beide Merkmale nur genau 2 Ausprägungen haben. Beispielsweise wurden 200 erkrankte Personen mit zwei verschiedenen Medikamenten (A und B) behandelt. Nach 4 Wochen wird geprüft, ob die Personen genesen sind oder weiterhin krank. Dies ergab:
Medikament A |
Medikament B |
Summe |
|
|---|---|---|---|
genesen |
70 |
80 |
150 |
krank |
10 |
40 |
50 |
Summe |
80 |
120 |
200 |
Hier bietet es sich an, Verhältnisse in den verschiedenen Gruppen/Untergruppen zu studieren:
Unter den mit Medikament A Behandelten ist die Anzahl der Genesenen 7 mal so groß wie die Anzahl der Kranken, d.h. unter den mit A Behandelten ist das Verhältnis von Genesenen zu Kranken 7:1 (7 zu 1)
Unter den mit Medikament B Behandleten ist das Verhältnis von Genesenen zu Kranken 2:1 (2 zu 1).
Unter den Genesenen ist das Verhältnis von Personen die Medikament A nehmen zu Personen die Medikament B nehmen 7:8.
Unter den Kranken ist das Verhältnis von Personen die Medikament A nehmen zu Personen die Medikament B nehmen 1:4.
Man nennen diese Verhältnisse Chancen (engl. odds). Stellt man sich vor alle Personen die Medikament A bekommen haben, sind in einem Raum und wir greifen eine Person zufällig heraus, so ist die Chance eine genesene Person zu ziehen \(7:1=7\). Bei der Gruppe die Medikament B bekommen haben ist die Chance eine genesene Person zu ziehen \(2:1\). Um nun zu quantifizieren wie unterscheidlich diese Verhältnisse zwischen den Gruppen sind, bildet man den Quotienten aus den Chancen:
Diese Zahl heißt Chancenverhältnis (engl. odds-ratio) und gibt an, wie stark sich die Chance eine genesene Person zu ziehen ändert, wenn zwischen der Gruppe mit Medikament A und der Gruppe mit Medikament B wechselt.
Genauer: Die Chance eine genesene Person zu ziehen ist unter den mit Medikament A Behandelten 3.5 mal höher als unter den mit Medikament B behandelten.
Die genau Definition:
Definition
Zu den beiden Merkmalen \(X\) und \(Y\) (mit je 2 Ausprägungen, \(A\),\(B\) bzw \(C\),\(D\)) sei eine Stichprobe erhoben wurden. Die zugehörigen Häufigkeiten seien in der folgenden Tabelle abgetragen:
C |
D |
Summe |
|
|---|---|---|---|
A |
\(h_{11}\) |
\(h_{12}\) |
\(h_{1\cdot}\) |
B |
\(h_{21}\) |
\(h_{22}\) |
\(h_{2\cdot}\) |
Summe |
\(h_{\cdot 1}\) |
\(h_{\cdot 2}\) |
\(n\) |
Das Chancenverhältnis ist dann definiert mittels:
Bedeutung:
\(\gamma=1\) heißt: die Chancen sind in beiden Gruppen gleich.
\(\gamma>1\) heißt: die Chancen sind in Gruppen A sind besser als in Gruppe B.
\(\gamma<1\) heißt: die Chancen sind in Gruppen B sind besser als in Gruppe A.
Der allgemeine Fall#
Für den Vergleich von nominalen Merkmalen von denen mindestens eins mehr als 2 Ausprägungen hat, lässt sich das Chancenverhältnis nicht berechnen. Hier geht man anders vor:
Wir stellen uns eine Kontingentafel vor, von der wir nur die Randhäufigkeiten kennen:
\(b_1\) |
\(\dots\) |
\(b_m\) |
\(\text{Summe}\) |
|
|---|---|---|---|---|
\(a_1\) |
? |
? |
? |
\(h_{1\cdot}\) |
\(\vdots\) |
? |
? |
? |
\(\vdots\) |
\(a_k\) |
? |
? |
? |
\(h_{k\cdot}\) |
\(\text{Summe}\) |
\(h_{\cdot 1}\) |
\(\dots\) |
\(h_{\cdot m}\) |
\(n\) |
Nun stellen wir uns die Frage, wie müsste die Tabelle ausgefüllt sein, wenn Zugehörigkeit zu den Gruppen \(Y=b_1\), … , \(Y=b_m\) keinen Einfluss auf die (prozentuale) Aufteilung auf die Gruppen \(X=a_1\), … , \(X=a_k\) hat. Wenn also beispielsweise \(20\%\) der gesamten Stichprobe die Ausprägung \(X=a_1\) aufweisen, so sollten auch in der Untergruppe (also der Spalte) \(Y=b_1\) genau \(20\%\) den Wert \(X=a_1\) aufweisen. Genauso sollten \(20\%\) von allen Werten aus der Spalte \(Y=b_2\) den Wert \(X=a_1\) aufweisen, usw.
Wenn das Merkmal \(Y\) keinen Einfluss auf \(X\) hat, so muss also für jedes \(i\) und jedes \(j\) gelten:
Umgestellt ergibt dies
Wenn also der Eintrag in der Kontingenztafel an Stelle \((i,j)\) genau dem Wert \(\frac{h_{i\cdot}h_{\cdot j}}{n}\) entspricht, so sind Größenverhältnisse der \(a_i\)’s in jeder \(b_j\)-Spalte gleich. Man sagt, die Merkmale \(X\) und \(Y\) haben dann keinen Einfluss aufeinander. Der Wert
ist als gerade die erwartete Häufigkeit, falls \(X\) und \(Y\) keinen Einfluss aufeinander haben
Die Maßzahl die wir nun betrachten wollen, sagt, wie weit wir von dieser Unabhängigkeit entfernt sind. Sie wird berechnet mittels
Im Zähler sehen wir die Differenz \(h_{ij}-e_{ij}\):
Wenn dieser Wert immer gleich Null ist sind, liegt „größtmögliche Unabhängigkeit“ vor. Dann ergibt sich \(\chi^2=0\).
Wenn die gemesse Häufigkeit \(h_{ij}\) immer sehr stark von der erwarteten Häufigkeit \(e_{ij}\) abweicht, ist der Wert im Zähler groß. Durch das Quadrat spielt das Vorzeichen der Abweichung keine Rolle. Daher liegt bei einer „großen Abweichung von Unabhängigkeit“ ein sehr großer Wert \(\chi^2\) vor.
Fazit: Der Wert \(\chi^2\) ist ein Maß für die Unabhängigkeit der beobachteten Merkmale. Ein kleiner Wert spricht für Unabhängigkeit, ein großer Wert für starke Abhängigkeit. Die Maßzahl \(\chi^2\) kann alle Werte aus \([0,\infty)\) annehmen.
Problem: Der Wert \(\chi^2\) hängt von den Dimenson der Tabelle ab und kann beliebig groß werden. So sind Kontingeztafeln unterschieldicher Dimension schwer vergleichbar. Einen Ausweg liefert der korrigierte Kontingenzkoeffizient:
Für \(K^*\) gilt nun \(0\leq K^* \leq 1\).
Wir fassen die eingefühten Größen noch einmal in der folgenden Definition zusammen
Definition
Wir betrachten ein bivariate Stichprobe der Größe \(n\) zu zwei nominalen Merkmalen. Dann heißt
der \(\chi^2\)-Koeffizient und
der korrigierte Kontingenzkoeffizient.
Nun schauen wir uns diese Größen anhand eines Beispiels an.
Beispiel
Die Jungs und Mädchen der 8. Klasse sollen sich beim Sportfest auf die drei Sporarten: Volleyball, Fussball und Handball aufteilen. Die Aufteilung ergab folgende Kontingenztabelle
Kontingenztabelle (2x3):
Volleyball |
Fussball |
Handball |
Summe |
|
|---|---|---|---|---|
Jungs |
10 |
20 |
30 |
60 |
Mädchen |
20 |
25 |
15 |
60 |
Summe |
30 |
45 |
45 |
120 |
Erwartete Häufigkeiten:
Die erwartete Häufigkeit berechnet sich nach der Formel \(e_{ij}=\frac{h_{i\cdot}h_{\cdot j}}{n}\). Wir tragen erwarteten Häufigkeiten in die Tabelle ein:
Volleyball |
Fussball |
Handball |
Summe |
|
|---|---|---|---|---|
Jungs |
\( \frac{60 \cdot 30}{120} = 15\) |
\(\frac{60 \cdot 45}{120} = 22.5\) |
\(\frac{60 \cdot 45}{120} = 22.5\) |
\(60\) |
Mädchen |
\(\frac{60 \cdot 30}{120} = 15\) |
\(\frac{60 \cdot 45}{120} = 22.5\) |
\(\frac{60 \cdot 45}{120} = 22.5\) |
\(60\) |
Summe |
\(30\) |
\(45 \) |
\(45\) |
\(120\) |
Berechnung des \(\chi^2\)-Wertes:
Die Formel lautet:
Einsetzen der Werte:
Berechnung des korrigierten Kontingenzkoeffizienten:
Es gilt
In diesem Beispiel ist \(M=\min\{2,3\}=2\) und \(\chi^2=8.\bar 8\). Daher gilt:
Fazit:
Der \(\chi^2\)-Wert beträgt 8.\bar 8.
Der korrigierte Kontingenzkoeffizient \(K^*\) beträgt 0.371.
Umsetzung in R#
Der 2x2 Fall: Chancenverhältnis#
# Erstellung einer 2x2 Kontingenztabelle
K <- matrix(c(30, 20, 10, 40), nrow = 2, byrow = TRUE)
rownames(K) <- c("Ereignis Ja", "Ereignis Nein")
colnames(K) <- c("Gruppe 1", "Gruppe 2")
K
# Manuelle Berechnung des Odds Ratios
a <- K[1, 1]
b <- K[1, 2]
c <- K[2, 1]
d <- K[2, 2]
odds_ratio <- (a / c) / (b / d)
# Ausgabe des Odds Ratios
cat("Odds-Ratio = ",odds_ratio)
| Gruppe 1 | Gruppe 2 | |
|---|---|---|
| Ereignis Ja | 30 | 20 |
| Ereignis Nein | 10 | 40 |
Odds-Ratio = 6
Der allgemeine Fall: \(\chi^2\)-Wert und Kontingenzkoeffizient#
# Erstellung einer 2x3 Kontingenztabelle
Ktab <- matrix(c(10, 20, 30, 20, 25, 15), nrow = 2, byrow = TRUE)
rownames(Ktab) <- c("Kategorie A", "Kategorie B")
colnames(Ktab) <- c("Gruppe 1", "Gruppe 2","Gruppe 2")
# Ausgabe der Tabelle
Ktab
# Berechnung des Chi^2-Werts
Ktab <- as.table(Ktab) # Umwandeln in Datentyp "table"
chi2_test <- chisq.test(Ktab) # Berechnung chi-quadrat-Test
chi2_value <- chi2_test$statistic # Extraktion des chi-quadrat-Werts
# Berechnung des Kontingenzkoeffizienten K
n <- sum(Ktab) # Gesamtzahl n berechnen
K <- sqrt(chi2_value / (chi2_value + n)) # Kontingenzkoeffizient
# Berechnung des korrigierten Kontingenzkoeffizienten K*
M <- min(dim(Ktab)) # Minimum aus Zeilen- und Spaltenzahl
Kstern <- K/sqrt((M-1)/M) # korr. Kontingenzkoeffizient
# Ausgabe der Werte
cat("Chi^2-Wert:", chi2_value, "\n\n")
cat("Korrigierter Kontingenzkoeffizient K*:", Kstern)
| Gruppe 1 | Gruppe 2 | Gruppe 2 | |
|---|---|---|---|
| Kategorie A | 10 | 20 | 30 |
| Kategorie B | 20 | 25 | 15 |
Chi^2-Wert: 8.888889
Korrigierter Kontingenzkoeffizient K*: 0.3713907