Mehr als 2 Merkmale

Es folgt ein Überblick über Methoden der deskriptiven Statistik für multivariate Daten, wenn mehr als 2 Merkmale gemessen/erhoben wurden. Zu beachten ist hier wieder welche Messbarkeit die erhobenen Merkmale haben.

Maßzahlen

Vektor mit Maßzahlen

Die Maßzahlen der univariaten Statistik können pro Merkmal erhoben werden und dann als Vektor oder Tabelle dargestellt werden. Liegen metrische Daten vor, so kann z.B. ein Mittelwertvektor gebildet werden. Dies ist zeigt natürlich nicht den Zusammenhang der Daten, sondern behandelt sie wie einzelne getrennt voneinander erhobene Stichproben.

Umsetzung in R

Hier bietet es sich an, den apply()-Befehl zu nutzen. Damit kann man eine Funktion auf die Spalten (oder Zeilen) eines data.frames anwenden.

apply(iris[,1:4], 2, mean)

Sepal.Length

5.84333333333333

Sepal.Width

3.05733333333333

Petal.Length

3.758

Petal.Width

1.19933333333333

Erkärung des Codes

• iris[,1:4] wählt die ersten 4 Spalten von iris aus. In der 5. Spalte stehen die Spezies, die möchten wir hier nicht betrachten.

• Die 2 steht für Spalten, d.h. wir wollen die Funktion auf die Spalten anwenden. Eine 1 würde bedeuten, dass wir die Funktion auf die Zeilen anwenden wollen.

• mean heißt die Funktion die wir auf jede einzelne Spalte anwenden wollen

Es ist auch möglich eine Funktion selbst zu definieren und diese in den apply-Befehl einzusetzen. Die ist zum Beispiel nötig, wenn wir den Variationskoeffizient pro Spalte ausrechnen wollen.

varkoeff <- function(x){ sd(x)/mean(x)}
apply(iris[, 1:4], 2, varkoeff)

Sepal.Length

0.14171125977944

Sepal.Width

0.142564201353041

Petal.Length

0.46974407484286

Petal.Width

0.635551141434419

Erkärung des Codes

• varkoeff <- function(x){ ... } bedeutet wir definieren eine neue Funktion. Sie soll varkoeff heißen. Hier kann man sich einen beliebigen Namen ausdenken. Der Ausdruck function(x) sagt, dass es eine Funktion ist und das Argument x heißt. In die geschweiften Klammern schreibt man, was die Funktion mit dem x macht, also die Bildungsvorschrift.

• sd(x)/mean(x) ist die Bildungsvorschrift in unserer Funktion: Berechne die Standardabweichung von x und teile diesen Wert durch das arithmetische Mittel von x.

Der summary-Befehl

Eine schnelle Übersicht über viele Maßzahlen liefert der Befehl summary().

summary(iris)

  Sepal.Length    Sepal.Width     Petal.Length    Petal.Width   
 Min.   :4.300   Min.   :2.000   Min.   :1.000   Min.   :0.100  
 1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300  
 Median :5.800   Median :3.000   Median :4.350   Median :1.300  
 Mean   :5.843   Mean   :3.057   Mean   :3.758   Mean   :1.199  
 3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.800  
 Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500  
       Species  
 setosa    :50  
 versicolor:50  
 virginica :50  
                
                
                

Kovarianzmatrix und Korrelationsmatrix

Zeigt die Kovarianzen (oder Korrelationskoeffizienten) zwischen allen Variablenpaaren (Diagonalen = Varianzen). Um dies zu verstehen, wiederholen Sie gern Maßzahlen im Abschnitt Zwei metrische Merkmale.

An Stelle \(i,j\) der Matrix steht die Kovarianz (oder der Korrelationskoeffizient) vom \(i\)-tem und \(j\)-tem Merkmal. Die Kovarianz (bzw Korrelation nach Pearson) lässt sich natürlich nur zwischen stetigen Merkmalen erheben. Auf der Diagonalen der Kovarianzmatrix steht jeweils die Varianz. Auf der Diagonalen der Korrelationsmatrix steht immer eine \(1\), denn dies ist der Korrelationskoeffizient von eine Spalte mit sich selbst.

Merke:

Kovarianzmatrix:

• An Stelle \((i,j)\) steht die Kovarianz von Spalte \(i\) und Spalte \(j\).

• Die Kovarianzmatrix ist symmetrisch: An Stelle \((i,j)\) steht immer der gleiche Wert wie an Stelle \((j,i)\).

• Auf der Diagonalen stehen die Varianzen: An Stelle \((i,i)\) steht die Varianz der Daten in Spalte \(i\).

Korrelationsmatrix:

• An Stelle \((i,j)\) steht der Korrelationskoeffizient von Spalte \(i\) und Spalte \(j\).

• Die Korrelationsmatrix ist symmetrisch: An Stelle \((i,j)\) steht immer der gleiche Wert wie an Stelle \((j,i)\).

• Auf der Diagonalen stehen immer \(1\)en.

Umsetzung in R

Wendet man die (schon bekannten) Befehle cov und cor auf einen data.frame mit metrischen Daten an, so wird die Korrelationsmatrix bzw die Kovarianzmatrix erstellt.

cov(iris[,1:4])

cor(iris[,1:4])

A matrix: 4 × 4 of type dbl

	Sepal.Length	Sepal.Width	Petal.Length	Petal.Width
Sepal.Length	0.6856935	-0.0424340	1.2743154	0.5162707
Sepal.Width	-0.0424340	0.1899794	-0.3296564	-0.1216394
Petal.Length	1.2743154	-0.3296564	3.1162779	1.2956094
Petal.Width	0.5162707	-0.1216394	1.2956094	0.5810063

A matrix: 4 × 4 of type dbl

	Sepal.Length	Sepal.Width	Petal.Length	Petal.Width
Sepal.Length	1.0000000	-0.1175698	0.8717538	0.8179411
Sepal.Width	-0.1175698	1.0000000	-0.4284401	-0.3661259
Petal.Length	0.8717538	-0.4284401	1.0000000	0.9628654
Petal.Width	0.8179411	-0.3661259	0.9628654	1.0000000

Graphische Darstellungen

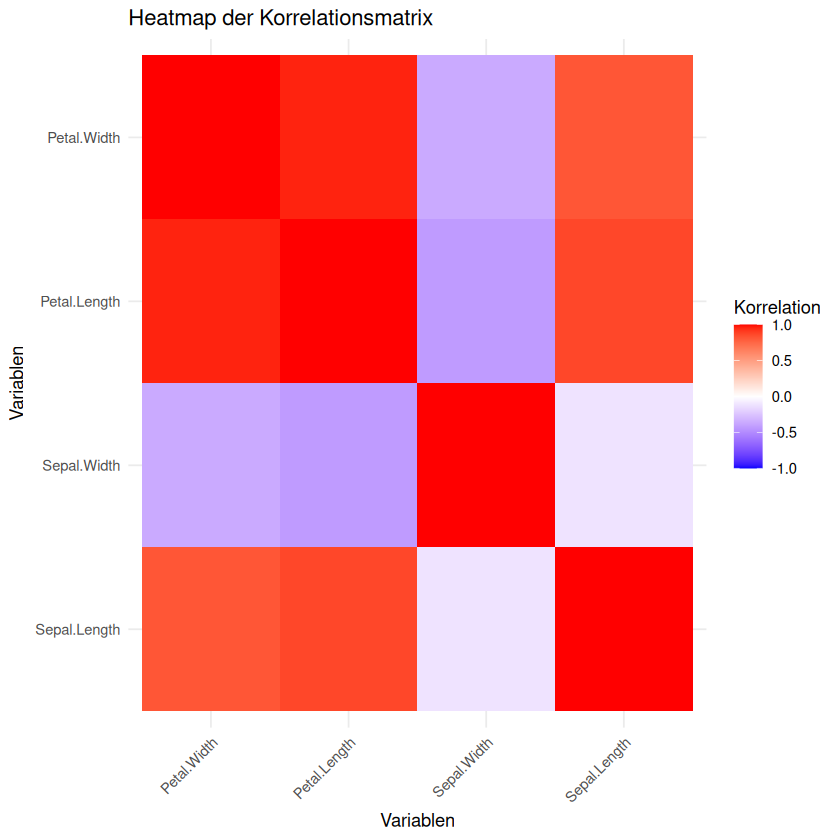
Heatmap

Eine Heatmap ist eine Art von visueller Darstellung, die verwendet wird, um komplexe Daten zu visualisieren und zu analysieren. Sie zeigt die Beziehungen zwischen verschiedenen Variablen oder Werten in einer Tabelle oder Matrix.

Eine Heatmap besteht aus einer Tabelle oder Matrix, in der jede Zelle einen Wert darstellt. Die Werte werden in einer Farbskala dargestellt, wobei die Helligkeit oder Intensität der Farbe die Größe oder Stärke des Wertes anzeigt. Die Farben können auch unterschiedliche Nuancen haben, um die Art der Beziehung zwischen den Variablen anzuzeigen.

Eine Heatmap für eine Korrelationsmatrix ist eine besondere Art von Heatmap, die verwendet wird, um die Korrelationen zwischen verschiedenen Variablen in einer Datenmenge zu visualisieren. Hier werden die Korrelationen zwischen den Variablen in einer Farbskala dargestellt. Dadurch kann man schnell erkennen, welche Variablen stark miteinander korreliert sind und welche nicht.

Umsetzung in R: Varinate 1 ohne zusätzliches Paket

# Korrelationsmatrix berechnen
korrelationsmatrix <- cor(iris[, 1:4])
# Heatmap zeichnen
heatmap(korrelationsmatrix,         # korrelationsmatrix ist Input
        symm=TRUE,                  # sagt, dass symm. Matrix eigegeben wird
        revC = TRUE,                # sort für die richtige Reihenfolge d. Zeilen
        Rowv = NA,Colv = NA,)       # kein Dendrogramm zeichnen

Umsetzung in R: Varinate 2 mit reshape2 und ggplot2

Mit ggplot2 sieht der Heatplot etwas moderner aus. Außerdem haben wir die Möglichkeit die eine Legende für die Farbscala hinzuzufügen.

library(ggplot2)
library(reshape2)

# Korrelationsmatrix berechnen
korrelationsmatrix <- cor(iris[, 1:4])

# Umstrukturieren der Matrix für ggplot2
korrelationsmatrix_melted <- melt(korrelationsmatrix)

ggplot(korrelationsmatrix_melted, 
       aes(factor(Var1, levels = rev(levels(Var1))), Var2, fill = value)) +
  geom_tile() +
  scale_fill_gradient2(low = "blue", high = "red", mid = "white", midpoint = 0, limit = c(-1, 1), space = "Lab", name = "Korrelation") +
  theme_minimal() +
  theme(axis.text.x = element_text(angle = 45, vjust = 1, hjust = 1)) +
  labs(title = "Heatmap der Korrelationsmatrix", x = "Variablen", y = "Variablen")

Erläuterung des Codes

• library(reshape2): Hier laden wir die Bibliothek reshape2, die wir später für die Umstrukturierung der Korrelationsmatrix benötigen.

• korrelationsmatrix <- cor(iris[, 1:4]): Berechnet die Korrelationsmatrix

• korrelationsmatrix_melted <- melt(korrelationsmatrix): Umstrukturierung der Matrix, so dass sie als Eingabe für ggplot2 passt. Die melt()-Funktion erstellt eine neue Tabelle, in der jede Zeile eine einzelne Zelle der ursprünglichen Matrix darstellt. Die neuen Spalten Var1 und Var2 enthalten die Namen der Variablen, die korreliert sind, und die Spalte value enthält die Korrelation zwischen den Variablen.

• ggplot(korrelationsmatrix_melted, ...) der plot Befehl von ggplot2

• aes() definiert die Ästhetik der Heatmap.

• Die factor()-Funktion wird verwendet, um die Variablen in der Var1-Spalte in der richtigen Reihenfolge anzuzeigen.

• Die geom_tile()-Funktion erstellt die Heatmap selbst.

• Die scale_fill_gradient2()-Funktion definiert die Farbskala für die Heatmap.

• Die theme_minimal()-Funktion passt die Optik leicht an (ist optional)

• Die theme()-Funktion setzt die Anzeige der Variablen in der Var1-Spalte.

• Die labs()-Funktion setzt den Titel und die Beschriftungen für die Heatmap.

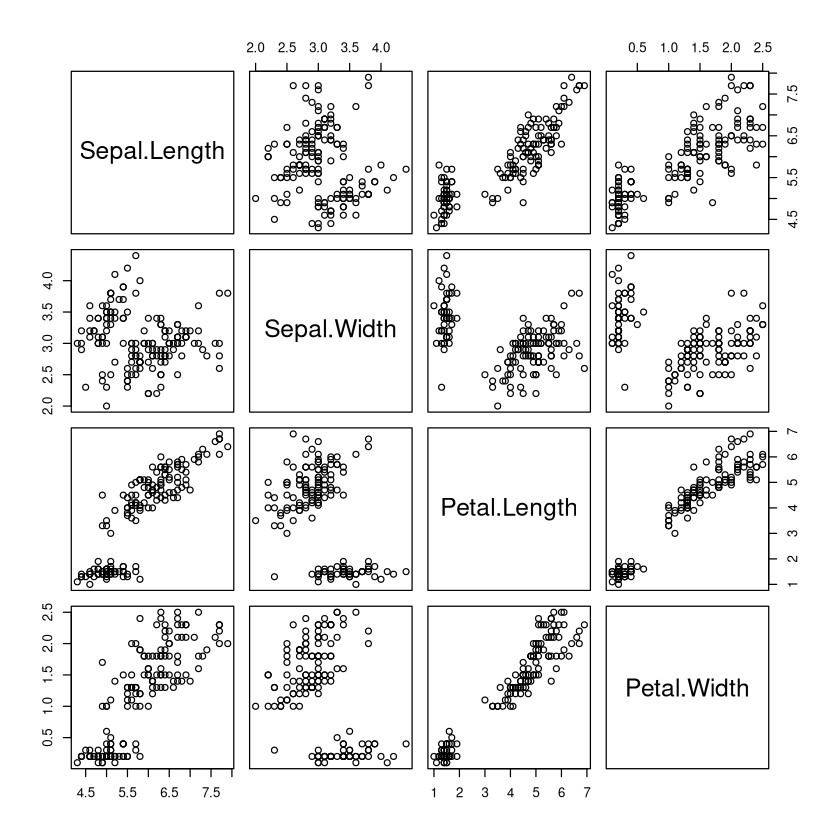
Streudiagramm-Matrix

Die paarweise Darstellung aller Streudiagramme der möglichen Variablenkombinationen.
Dies ist schnell erreicht mit dem Befehl pairs().

pairs(iris[,1:4])

3D-Streudiagramme

Für drei Variablen lässt sich noch ein Streudiagramm zeichnen. Die ist auch möglich mit Interaktion/Rotation. Halten Sie dazu in der Grafik die linke Maustaste gedrückt und bewegen Sie den Curser.

Wir plotten zunächst 3 Merkmale aus dem iris- Datensatz. Die Färbung wird entsprechend der Spezies vorgenommen.

library(plotly)     # Paket für 3d-Plots

Show code cell output Hide code cell output

Attache Paket: ‘plotly’

Das folgende Objekt ist maskiert ‘package:ggplot2’:

    last_plot

Das folgende Objekt ist maskiert ‘package:stats’:

    filter

Das folgende Objekt ist maskiert ‘package:graphics’:

    layout

plot_ly(data = iris ,         # plot_ly ist der Plot-Befehl aus "plotly", 
        x = ~Sepal.Length,    # data= legt Datensatz fest
        y = ~Sepal.Width,     # x,y,z = ordnet den Achsen die Spalte zu
        z = ~Petal.Width,     #
        color = ~Species,     # Farbe entsprechend der Spezies
        type="scatter3d",     # es soll ein 3d-Plot entstehen
        mode="markers",       # werte sollen als Punkte dargestellt werden
        size = 0.2)           # Größe der Punkte

# Ein weiteres Beispiel mit zufälligen Daten
set.seed(123)                                 # damit bleibt der Zufall jedes mal gleich
temp     <- rnorm(100, mean=30, sd=5)         # zufällige Temperaturen auswürfeln
pressure <- rnorm(100)                        # zufälligen Druck auswürfeln
dtime    <- 1:100                             # Zeitpunkte zuordnen
plot_ly(x=temp, y=pressure, z=dtime, 
        type="scatter3d", mode="markers", 
        color=temp)                           # Farbe entsprechend der Temperatur

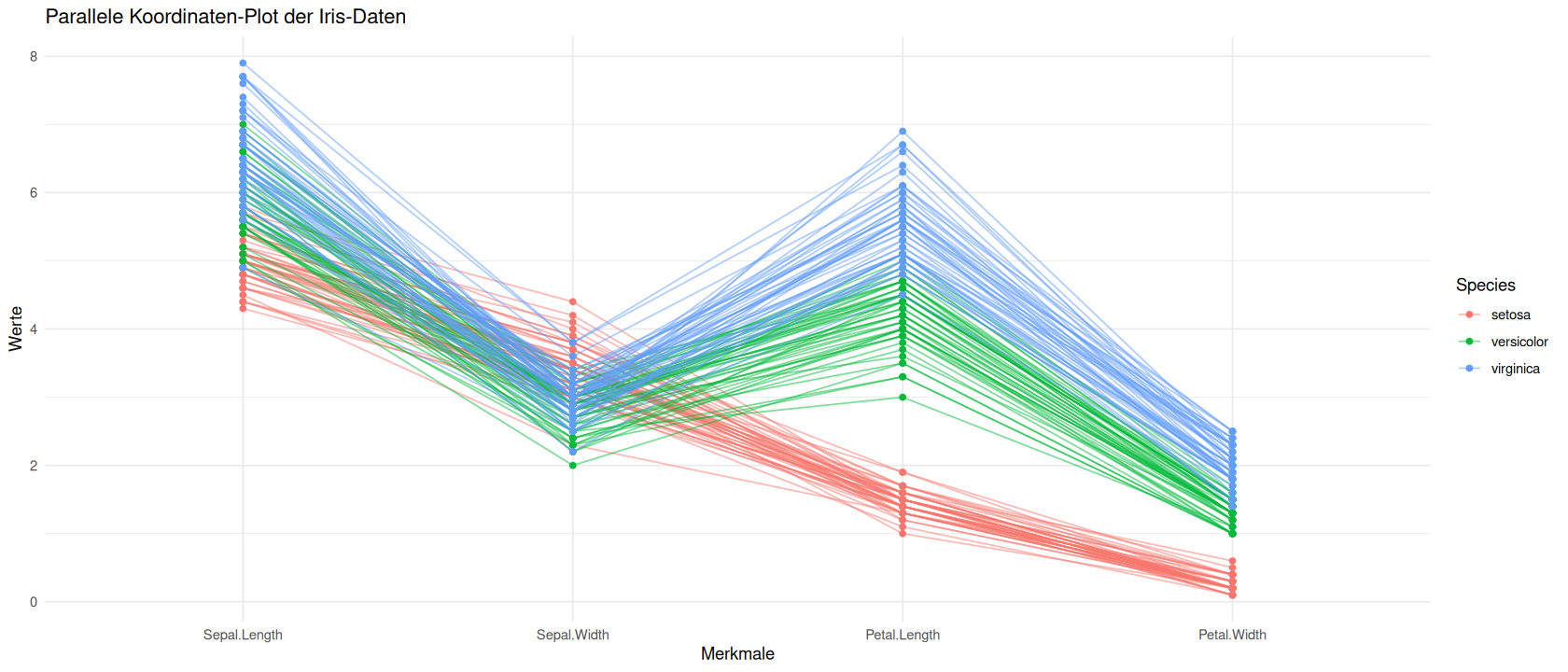
Parallele Koordinaten

Was ist ein Parallel Coordinate Plot?

Ein Parallel Coordinate Plot (deutsch: Parallele Koordinaten-Diagramm) ist eine Visualisierungsmethode zur Darstellung mehrerer numerischer Variablen gleichzeitig. Dabei wird jede Variable auf einer eigenen vertikalen Achse dargestellt, und jede Beobachtung (Zeile im Datensatz) wird als Linie gezeichnet, die die Werte der Beobachtung über die Achsen hinweg verbindet.

Diese Diagrammart eignet sich besonders zur Darstellung von multivariaten Daten mit mehreren numerischen Variablen. Alle Variablen werden auf parallelen Achsen gezeigt, um Muster in Beobachtungen zu erkennen.

Wie erstellt man einen Parallel Coordinate Plot in R?

Für die Erstellung von Parallel Coordinate Plots in R wird häufig das Paket GGally verwendet, das eine Erweiterung von ggplot2 ist. Wir zeigen dies am Beispiel des iris Datensatz.

library(ggplot2)  # Pakte um schöne Grafiken zu erstellen
library(GGally)   # Paket um den Parallel-Koordianten-Plot zu erstellen

Registered S3 method overwritten by 'GGally':
  method from   
  +.gg   ggplot2

options_orig<-options()            # Anzeigeoptionen speichern
options(repr.plot.width = 14, repr.plot.height = 6)   # Anzeigeoptionen ändern (Breite Grafik)
# Parallel Coordinate Plot
ggparcoord(data = iris,
           columns = 1:4,          # Die Spalten 1 bis 4 (numerische Variablen)
           groupColumn = 5,        # Gruppierung nach Species
           scale = "globalminmax", # Werte auf gleiche Skala bringen
           alphaLines = 0.5,       # Transparenz der Linien
           showPoints = TRUE) +    # Punkte für einzelne Werte anzeigen
  labs(title = "Parallele Koordinaten-Plot der Iris-Daten",
       x = "Merkmale",             # Titel und Achsen
       y = "Werte") +              # Bezeichnungen
  theme_minimal()                  # optionale optische Anpassung
options(options_orig)              # Anzeigeoptionen zurücksetzen

Interpretation

Beim Interpretieren eines Parallel Coordinate Plots achtet man auf folgende Aspekte:

• Gruppenunterschiede: Linien von verschiedenen Gruppen (z.B. Arten) haben oft ähnliche Verläufe.

• Korrelationen: Wenn zwei benachbarte Achsen fast parallele Linien zeigen, deutet dies auf eine positive Korrelation hin. Kreuzen sich die Linien häufig, könnte eine negative Korrelation vorliegen.

• Ausreißer: Einzelne Linien, die sich stark von den anderen unterscheiden, können auf Ausreißer hinweisen.

• Streuung: Eine breite Streuung der Linien zeigt eine hohe Varianz in den Daten.

Vor- und Nachteile

Vorteile	Nachteile
Darstellung vieler Variablen	Schwer lesbar bei großen Datenmengen
Vergleich von Gruppen möglich	Interpretation kann schwierig sein
Identifikation von Ausreißern möglich	Linien können sich stark überlagern
Visualisierung von Korrelationen	Reihenfolge der Achsen beeinflusst das Ergebnis