Übung 3#
1. Maßzahlen berechnen#
Nutzen Sie den R-internen Datensatz airquality und hier insbesondere die Spalte Temp.
In welcher Einheit ist die Temperatur gegeben? Rechnen Sie diese in Grad-Celsius um.
Berechnen Sie von der Temperatur (in Grad-Celsius):
Median (Lösung: \(26.11\))
Mittelwert (Lösung: \(25.490196\))
Standardabweichung (Lösung: \(5.25848\))
Varianz (Lösung: \(27.65165\))
Schiefe (Lösung: \(-0.3741\))
\(0.8\)-Quantil (Lösung: \(30\))
Variationskoeffizient (Lösung: \(0.20629\))
Spannweite (Lösung: \(22.7778\))
IQR (Lösung: \(7.2222\))
Welche Einheiten haben die berechneten Größen?
# Platz zum Rechnen
2. Klasseneinteilung#
Mit dem Befehl cut() lässt sich eine Stichprobe in Klassen einteilen. Wie in der Vorlesung besprochen, wird dies typischerweise bei stetigen Merkmalen und bei diskreten Merkmalen mit vielen Ausprägungen nötig.
Aufgaben:
Teilen Sie die Daten in dem Vektor x mithilfe des Befehls cut() in Klassen ein.
Geben Sie dabei einmal nur die Anzahl der Klassen vor.
Geben Sie in einem anderen Versuch die genauen Klassengrenzen ein. Wann entstehen Werte
NAund was bedeuten diese?Verschaffen Sie sich einen Überblick über das Ergebnis von
cut()indem Sie eine Häufigkeitstabelle erstellen.
x<-c(39.5, 17.2, 41.7, 6.5, 21.1, 53.8, 15, 29.4,
48.1, 51.5, 17.7, 7.3, 13.1, 29.4, 44.3, 16.6,
57.3, 71.8, 51.4, 74.2, 84.3, 32.9, 81.5,
18.8, 29.5, 67, 68.7, 40.6, 44.9, 38.5, 11.9,
10.3, 58.2, 40.9, 23.6, 70.7, 18.8, 43.8,
68.1, 44.5, 61.7, 64.6, 46.3, 50.8, 57.9,
61.5, 52.1, 15.9, 15, 33.4, 22.2, 20.7, 52.7,
31.1, 26.2, 54.7, 65.4, 42.7, 48.2, 38, 35.9,
70.5, 38.8, 50.6, 46.3, 55.4, 75.2, 2.2, 38.6,
46.2, 85, 29.6, 44.8, 15.1, 73.6, 56.5, 32.2,
1, 38.3, 59, 17.4, 67.3, 47.5, 46.7, 39.6,
33.7, 55.3, 7.6, 35.8, 47, 17.9, 37.3, 28.7,
69.6, 58.7, 42.7, 35.2, 61.4, 56, 34.1)
3. Histogramme#
Histogramme geben einen guten und schnellen Überblick über einen Datenvektor (mit metrischen Daten).
Aufgaben
Datensatz wählen
Wir verwenden hier eingebauten R-Datensatz
airquality. Schauen Sie sich mithead()die ersten Zeilen des Datensatzes an. Was bedeuten die EinträgeNA?Geben mit
hist()ein Histogramm mit fürOzoneaus.Passen Sie den Titel an.
Schreiben Sie an die y-Achse die dargestellte Größe und die Einheit.
Ändern Sie die Farbe der Säulen in ihre Lieblingsfarbe.
Erstellen Sie nun ein Histogramm für
Ozone, bei welchem Sie genau vorgeben welche Klassengrenzen zu wählen sind.Teilen Sie die Daten in Gruppen basierend auf der Windgeschwindigkeit ein:
Gruppe 1: Tage mit niedriger Windgeschwindigkeit (Windgeschwindigkeit kleiner als der Median)
Gruppe 2: Tage mit hoher Windgeschwindigkeit (Windgeschindigkeit größer-gleich dem Median)
Speichern Sie die Datensätze unter als Variablen
air1undair2ab.Histogramme erstellen
Erstellen Sie zwei Histogramme für die Ozonwerte (Ozone) der beiden Gruppen.
Achten die Darauf, dass in beiden Histogrammen die gleiche Klasseneinteilung vorgenommen wird.
Vergeben Sie sinnvolle Titel und Achsenbeschriftungen
Passen Sie auch die Farbe an.
Fügen Sie ein Gitternetz hinzu.
Diskutieren Sie (mit Ihrem Nachbarn) die Unterschiedliche in den Verteilungen der Ozonwerte zwischen den Gruppen.
Berechnen Sie jeweils 3 sinnvolle statistische Maßzahlen um Ihre Beobachtung zu quantifizieren.
# Platz zum Rechnen
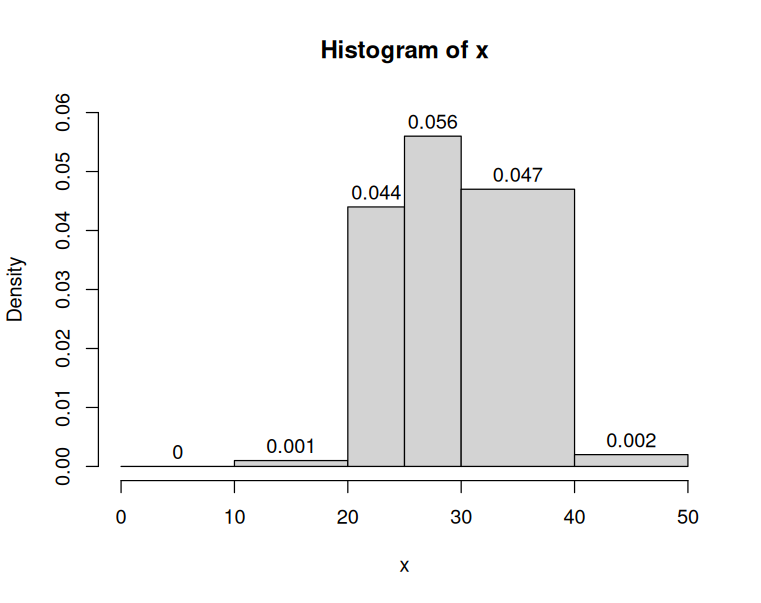
Histogramme mit unterschiedlicher Klassenbreite: In der folgenden Grafik ist eine Histogramm mit unterschiedlicher Klassenbreite zu einer Stichprobe der Größe 200 zu sehen.
Füllen Sie die Häufigkeitstabelle aus:
[0,10)
[10,20)
[20,25)
[25,30)
[30,40)
[40,50)
relative Häufigkeit
absolute Häufigkeit
4. Boxplots und empirische Verteilungsfunktionen#
Betrachten Sie wieder den Datensatz airquality.
Erstellen Sie einen Boxplot der Ozon-Werte.
Erstellen Sie zwei Boxplots in einer Grafik für die Ozon-Werte:
in einem werden die Ozonwerte für Tage mit Temperaturen \(>26\) Grad Celsius betrachtet
in dem anderen werden die Temperaturen \(\leq 26\) Grad Celsius betrachtet
Leiten Sie aus der Grafik einen möglichen Zusammenhang zwischen Temperatur und Ozongehalt ab.
Wir wiederholen dies nun mit der Verteilungsfunktion
Erstellen Sie für eine Verteilungsfunktion für die Ozon-Wert in
airquality.Erstellen Sie zwei Verteilungsfunktionen in einer Grafik für die Ozon-Werte:
in einer werden die Ozonwerte für Tage mit Temperaturen \(>26\) Grad Celsius betrachtet
in der anderen werden die Temperaturen \(\leq 26\) Grad Celsius betrachtet
Hinweis: mit dem Befehl
lines()wird in eine bestehende Grafik geplottet.Die Lösung zu 4. sollte etwa folgendermaßen aussehen:
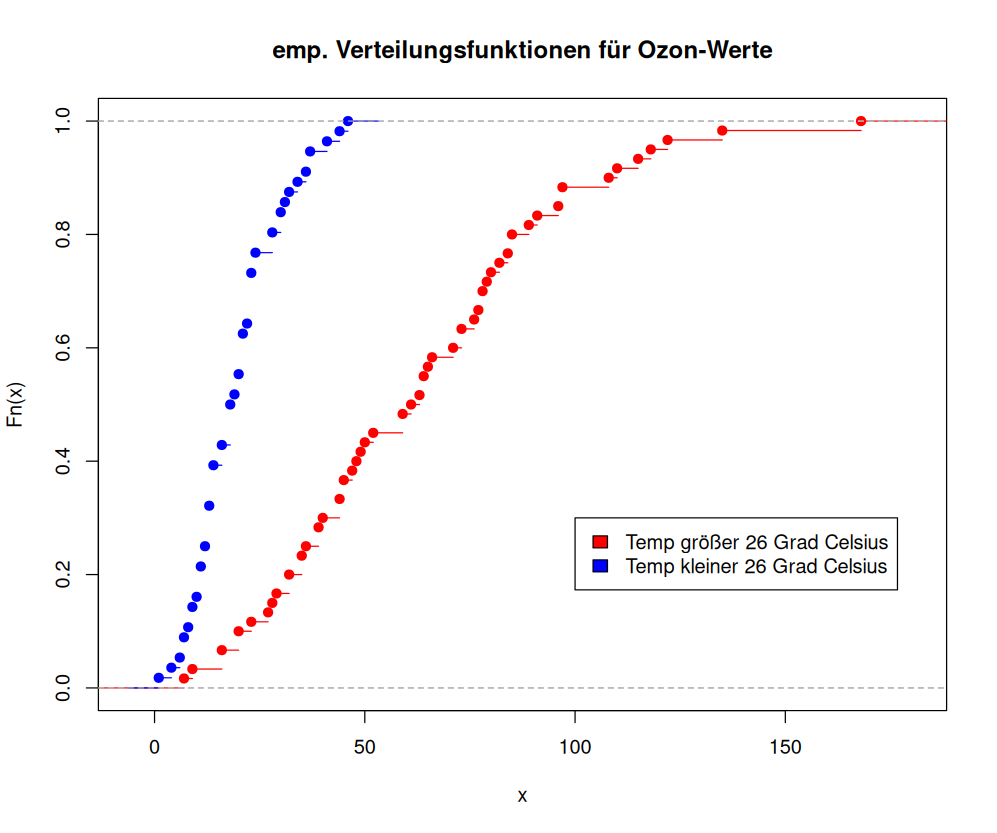
# Platz zum Rechnen


