Dreiecksverteilung

Dreiecksverteilung#

Definition#

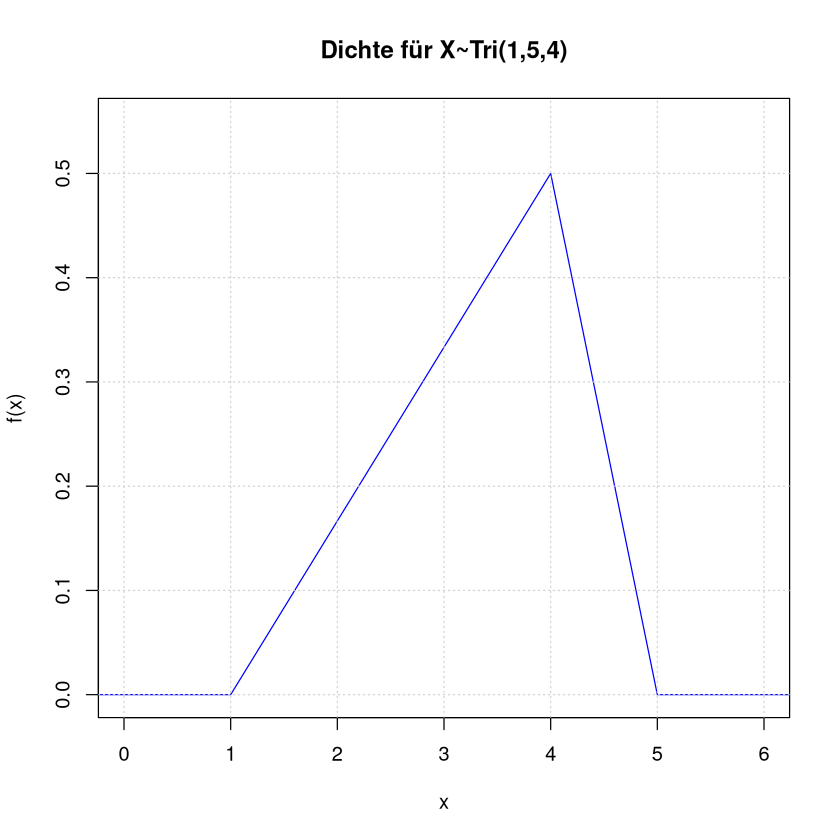
Diese Verteilung hat ihren Namen vom Verlauf der Dichtefunktion. Diese ist in folgender Grafik dargestellt:

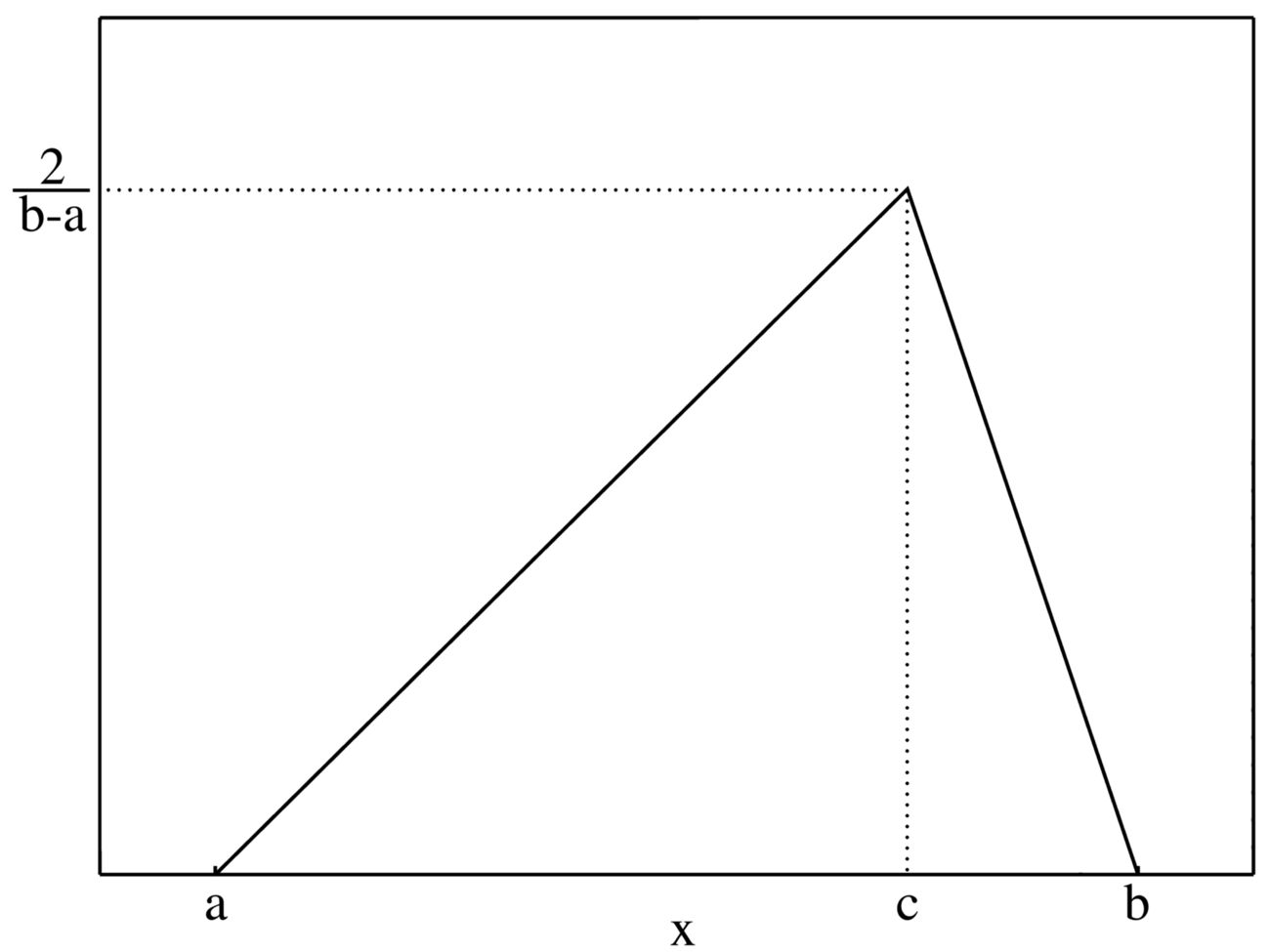
dreiecksvert

Die Parameter \(a\), \(b\) und \(c\) kann man anpassen. Zu beachten ist jedoch, dass \(a< c< b\) gelten soll. Der Wert \(\frac{2}{b-a}\) ist genau so gewählt, dass die Fläche unter der Funktion gleich \(1\) ist.

Die in der Grafik dargestellte Dichtefunktion ist explizit in der folgenden Definition gegeben.

Definition

Sei \(a\), \(b\) und \(c\) reelle Zahlen mit \(a<b<c\). Eine Zufallsvariable \(X\) welche mit der Wahrscheinlichkeitsdichte

\[\begin{split}f:\mathbb R\to\mathbb R,\qquad f(x)=\begin{cases} \frac{2(x-a)}{(b-a)(c-a)} & \text{falls } a\leq x\leq c\\ \frac{2(b-x)}{(b-a)(b-c)} & \text{falls } c< x\leq b\\ 0 & \text{sonst.} \end{cases}\end{split}\]

verteilt ist, heißt Dreieck-verteilt. Wir schreiben dann kurz

\[X\sim \mathrm{Tri}(a,b,c)\]

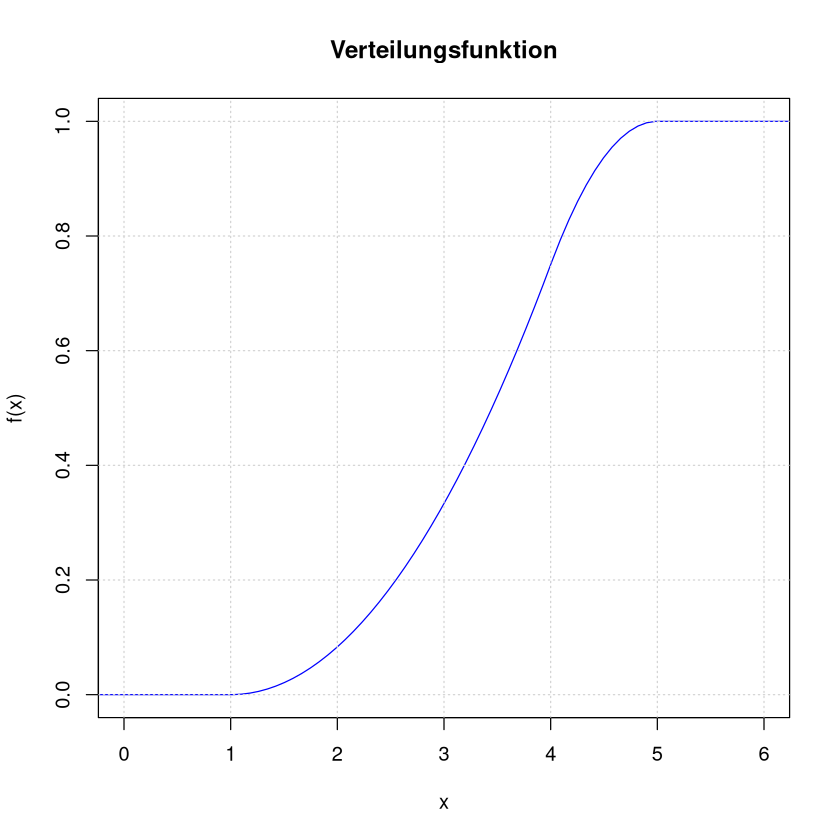
Die Verteilungsfunktion ist dann

\[\begin{split}F:\mathbb R \to [0,1],\qquad F(x)=\begin{cases} 0 & \text{falls }x<a \\ \frac{(x-a)^2}{(b-a)(c-a)} & \text{falls } a\leq x\leq c\\ 1-\frac{(b-x)^2}{(b-a)(b-c)}& \text{falls } c< x\leq b\\ 1 & \text{falls }x>b \end{cases} \end{split}\]

Anwendungen#

Es folgen ein paar Situationen in oft mit der Dreiecksverteilung gearbeitet wird:

  • Schätzungen von Projektzeiten Bei einer Aufgabe wird eine minimale (optimistische), eine typische (wahrscheinlichste) und eine maximale (pessimistische) Dauer angegeben. Die Dauer ist oft dreiecksförmig verteilt.

  • Fehlertoleranz in der Fertigung Ein Produktionsprozess hat eine Maßabweichung, die sich zwischen einer minimalen und maximalen Grenze bewegt, die typische Abweichung liegt etwa in der Mitte zwischen diesen beiden Werten.

  • Lieferschätzungen im E-Commerce Die Lieferzeit für ein Paket liegt zwischen 2 und 7 Tagen, mit einer wahrscheinlichsten Lieferzeit von etwa 4 Tagen.

  • Kraftstoffverbrauch eines Fahrzeugs Der Verbrauch eines Autos pro 100 km schwankt zwischen 5 und 10 Litern, mit einem wahrscheinlichsten Wert von etwa 7 Litern (unter normalen Bedingungen).

Eigenschaften#

Gilt \(X\sim \mathrm{Tri}(a,b,c)\), so gilt

\[ \mathbb E(X)= \frac{a+b+c}{3} \]
\[ \mathrm{Var}(X)= \frac{(a-b)^2+(b-c)^2+(a-c)^2}{36} \]

Wahrscheinlichkeitsdichte

Hide code cell source 
plot(c(-1,1,4,5,7),c(0,0,0.5,0,0),type = "l",
     col="blue",xlim=c(0,6),ylim=c(0,0.55),
     main="Dichte für X~Tri(1,5,4)",
     xlab="x",ylab="f(x)"
    )
grid()
../_images/0a3a79ed3236d8ec7cb46439933db66d346486382f2add73b9e75b4e2bf0675b.png

Verteilungsfunktion

Hide code cell source 
library(extraDistr)
q <- seq(from = -1,to=7,length.out = 100)
plot(q,ptriang(q,1,5,4),type="l",
     col="blue",xlim=c(0,6),
     main="Verteilungsfunktion",
     xlab="x",ylab="f(x)")
grid()
../_images/7cf2992bee696678b18f3618ceaba17b708c092d0108e7b9bd44ba03a0a8ba6a.png

Beispiel#

Beispiel: Kraftstoffverbrauch eines Fahrzeugs

Ein Auto verbraucht je nach Fahrweise und äußeren Bedingungen unterschiedlich viel Kraftstoff.

  • Minimaler Verbrauch: 5 Liter pro 100 km (unter optimalen Bedingungen).

  • Maximaler Verbrauch: 10 Liter pro 100 km (bei hoher Last oder ungünstigen Bedingungen).

  • Wahrscheinlichster Verbrauch: 7 Liter pro 100 km (bei normaler Fahrt).

Um dies zu modellieren soll der Verbrauch \(X\) einer Dreiecksverteilung folgen mit den Parametern:

  • \(a = 5\) (Minimum)

  • \(b = 10\) (Maximum)

  • \(c = 7\) (Maximalstelle der Dichte)

  1. Wie hoch ist die Wahrscheinlichkeit, dass der Verbrauch höchstens 6 Liter pro 100 km beträgt?

  2. Wie hoch ist die Wahrscheinlichkeit, dass der Verbrauch zwischen 6 und 8 Litern liegt?

  3. Wie groß muss \(t\) sein, damit die Wahrscheinlichkeit, dass der Verbrauch kleiner als \(t\) ist, genau \(0.9\) beträgt?

  4. Wie groß ist der Erwartungswert des Kraftstoffverbrauchs?

Lösung

  1. Angeben der Zufallsvariable

\(X\) … Der zufällige Verbrauch in Liter pro 100 km.

\(X\sim \mathrm{Tri}(5,10,7)\)

  1. Die Verteilungsfunktion

\[\begin{split} F(x) = \begin{cases} 0 &\text{falls } x < 5 \\ \frac{(x-5)^2}{10} &\text{falls } 5 \leq x \leq 7 \\ 1 - \frac{(10-x)^2}{15} &\text{falls } 7 < x \leq 10 \\ 1 &\text{falls } x > 10 \end{cases} \end{split}\]

  1. Berechnung der konkreten Antworten:

    • Aufgabe 1: Gesucht ist \(\mathbb P(X \leq 6)\)

      \[\mathbb P(X \leq 6) = F(6)= \frac{(6-5)^2}{10} = \frac{1^2}{10} = 0.1\]

      Antwort: Die Wahrscheinlichkeit, dass der Verbrauch höchstens 6 Liter pro 100 km beträgt, ist 0.1 (10%).

    • Aufgabe 2: Gesucht ist \(\mathbb{P}(6 \leq X \leq 8)\)

      \[ \mathbb{P}(6 \leq X \leq 8) = F(8) - F(6) \]

      Da \(8\) im Bereich \(7 < x \leq 10\) liegt:

      \[ F(8) = 1 - \frac{(10-8)^2}{15} = 1 - \frac{2^2} {15} = 1 - \frac{4}{15} = \frac{11}{15} \approx 0.733 \]

      Daher gilt

      \[ \mathbb{P}(6 \leq X \leq 8) = 0.733 - 0.1 = 0.633 \]

      Antwort: Die Wahrscheinlichkeit, dass der Verbrauch zwischen 6 und 8 Litern liegt, beträgt 0.633 (63.3%).

    • Aufgabe 3: Gesucht ist das 0.9-Quantil der Verteilung.

      Setze \(0.9=F(t)\) und löse nach \(t\) auf. Da wir nicht wissen, in welchem Intervall \([5,7]\) oder \((7,10]\) das Ergebnis liegen wird müssen wir beide ausprobieren:

      • Fall \([5,7]\): Löse \(0.9=\frac{(t-5)^2}{10}\). Dies ergibt \(t_1=2\) und \(t_2=8\). Beide liegen nicht im Intervall.

        → Das 0.9-Quantil liegt nicht im Intervall \([5,7]\).

      • Fall \((7,10]\): Löse \(0.9=1-\frac{(10-t)^2}{15}\). Dies ergibt

        \[0.1= \frac{(10-t)^2}{15} \quad \Leftrightarrow \quad 1.5=(10-t)^2\]

        also \(t_1= 8.7752\) und \(t_2=11.2247\). Für \(t_1\in (7,10]\) gilt.

        → Das gesuchte Quantil ist:

      \[t= 8.7752 \]

    • Aufgabe 4: Gesucht ist der Erwartungswert \(E(X)\)

      \[ E(X) = \frac{a + b + c}{3} = \frac{5 + 10 + 7}{3} = \frac{22}{3} \approx 7.33 \]

      Antwort: Der erwartete Kraftstoffverbrauch beträgt 7.33 Liter pro 100 km.

Umsetzung mit R#

Hier nutzen wir das Paket extraDistr um effizient mit der Dreiecksverteilung zu rechnen.

library(extraDistr)
# Aufgaben 1,2 und 3 aus dem Beispiel berechnet man 
# in R wie folgt
# Aufgabe 1
ptriang(6,a=5,b=10,c=7)
# Aufgabe 2
ptriang(8,a=5,b=10,c=7)-ptriang(6,a=5,b=10,c=7)
# Aufgabe 3
qtriang(0.9,a=5,b=10,c=7)
0.1
0.633333333333333
8.77525512860841

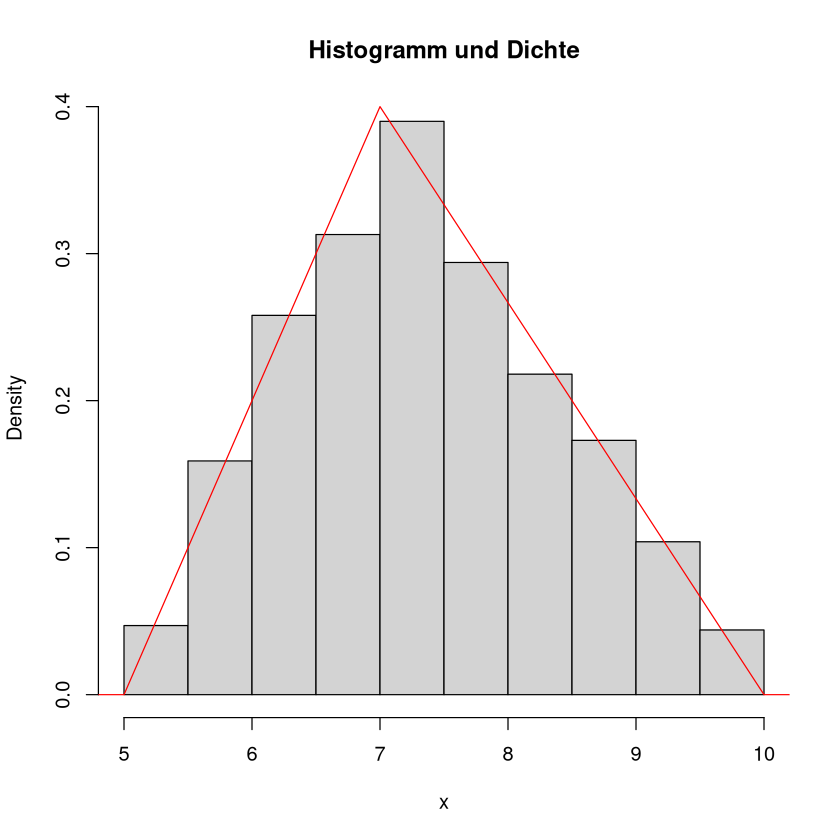
Wir erzeugen nun Zufallszahlen und erstellen ein Histogramm mit den relativen Häufigkeiten.

set.seed(457)
x<-rtriang(2000, 5, 10, 7)
hist(x,probability = TRUE,main="Histogramm und Dichte")
points(c(0,5,7,10,15),c(0,0,2/5,0,0),type="l",col="red")
../_images/b03e1e3314c5e41b37b32d67dbe87b137430350b7fd37ad91622321fe9105456.png