Konzentrationmaße

Was soll gemessen werden?

Ein Konzentrationsmaß misst, wie ungleich eine bestimmte Größe (z. B. Einkommen, Marktanteile oder Bevölkerung) innerhalb einer Gruppe verteilt ist. Es zeigt also, ob eine Ressource stark konzentriert oder gleichmäßig verteilt ist.

Beispiele

• Einkommensverteilung:

  • Wenn in einer Stadt 100 Menschen leben und jeder genau 2.000 € im Monat verdient, ist die Verteilung gleichmäßig – die Konzentration ist niedrig.

  • Wenn aber ein Mensch 100.000 € hat und die anderen 99 nur je 500 €, dann ist die Konzentration hoch, weil wenige viel besitzen und viele wenig.

• Marktanteile:

  • Wenn zehn Firmen jeweils 10 % des Marktes kontrollieren, ist die Konzentration gering.

  • Wenn aber eine Firma 91 % und die anderen neun je nur 1 % haben, ist der Markt stark konzentriert (Monopol-Tendenz).

• Bevölkerungsverteilung in Städten:

  • Wenn ein Land nur aus Städten besteht mit etwa der gleichen Eingwohnerzahl, ist die Bevölkerung gleichmäßig verteilt (niedrige Konzentration).

  • Wenn fast alle Menschen in einer einzigen Mega-Stadt leben und der Rest des Landes dünn besiedelt ist, ist die Konzentration hoch.

Um diese Art von Konzentration in Zahlen zu fassen lernen wir hier 2 Maßzahlen kennen:

• den Gini-Koeffizient

• den Herfindahl-Index

Außerdem werden wir eine graphische Visualisierung der Konzentration kennenlernen, die Lorenzkurve.

Lorenzkurve

Hier gehen wir davon aus, dass die Daten in Form einer geordneten Liste

\[ x_1 \leq x_2 \leq \dots \leq x_n \]

aus nicht-negativen Werten vorliegen. Die Lorenzkurve visualisiert - für jedes k - welchen Anteil die \(k\) kleinsten Wert an der Gesamtsumme haben, also für \(1\leq k\leq n\)

\[ \frac{x_1+ \dots + x_k}{x_1+ \dots + x_n} \]

Definition

Zu einer gegebenen Liste \( x_1 \leq x_2 \leq \dots \leq x_n \) aus nicht-negativen Zahlen heißt der Streckenzug durch die Punkte

\[(0,0), (u_1,v_1), \dots ,(u_n,v_n)=(1,1)\]

Lorenzkurve, wobei

\[u_k= \frac{k}{n} \quad \text{ und }\quad v_k=\frac{x_1+\dots+x_k}{x_1+\dots+x_n}\]

Stellen wir uns vor \(x_1,\dots,x_n\) beschreibt die Marktanteile von \(n\) Unternehmen. Der Gesamtmarkt habe die Größe \(x_1+\dots+x_n\). Dann ist

• \(u_k\) der Anteil \(k\) kleinsten Marktteilnehmer

• \(v_k\) der kummulierte Marktanteil für die \(k\) kleinsten Marktteilnehmer

Beispiel

Angenommen, wir haben 5 Haushalte mit folgendem monatlichen Einkommen (in Euro):

Haushalt	Einkommen (in Euro)
A	\(4000\)
B	\(2000\)
C	\(1000\)
D	\(3000\)
E	\(10000\)

Zuerst ordnen wir die Stichprobe:

\[ x_1=1000, \quad x_2=2000,\quad x_3= 3000,\quad x_4=4000, \quad x_5=10000\]

Das Gesamteinkommen beträgt:

\[ 1000 + 2000 + 3000 + 4000 + 10000 = 20000 \]

Die Berechnung der \(u_k\) und \(v_k\):

Index \(k\)	\(u_k\)	Einkommen (sortiert)	Anteil am Ges.Einkommen	\(v_k\)
\(1\)	\(\frac15=0.2\)	\(1000\)	\(\frac{1}{20}\)	\(\frac{1}{20}=0.05\)
\(2\)	\(\frac25=0.4\)	\(2000\)	\(\frac{2}{20}\)	\(\frac{3}{20}=0.15\)
\(3\)	\(\frac35=0.6\)	\(3000\)	\(\frac{3}{20}\)	\(\frac{6}{20}=0.3\)
\(4\)	\(\frac45=0.8\)	\(4000\)	\(\frac{4}{20}\)	\(\frac{10}{20}=0.5\)
\(5\)	\(\frac55=1\)	\(10000\)	\(\frac{10}{20}\)	\(\frac{20}{20}=1\)

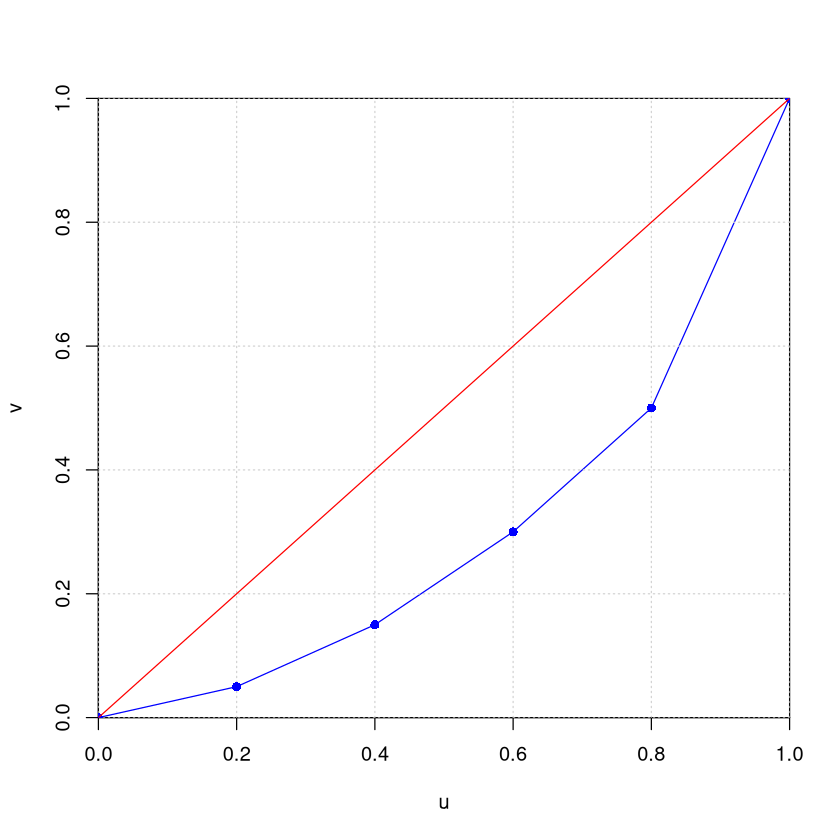
Die Lorenzkurve verläuft also durch die Punkte

\[(0,0), \quad (0.2,0.05), \quad (0.4,0.15), \quad (0.6,0.3), \quad (0.8,0.5), \quad (1,1)\]

Im folgenden R-Code wird diese Lorenzkurve erstellt.

Umsetzung in R

# Einkommenswerte (aufsteigend sortiert)
einkommen <- c(1000, 2000, 3000, 4000, 10000)
n         <- length(einkommen)                # Stichprobengröße
u         <- (0:n)/n                          # u-Vektor
f         <- einkommen/sum(einkommen)         # Anteil des Gesamteinkommens
v         <- c(0,cumsum(f))            # kummulierter Anteil des Gesamteinkommens
rbind(u,v)                                    # klebt u und v zu Matrix zusammen

# Plot-Befehle:
plot(u,v, type="l", xlim=c(0,1), ylim=c(0,1), xaxs="i", yaxs="i", col="blue", main="Lorenzkurve") # Lorenzkurve
grid()                                        # Gitter
points(u, v, pch=16, col="blue")              # Punkte an den Knicken hinzufügen
abline(0,1, col="red")                        # Diagonale

A matrix: 2 × 6 of type dbl

u	0	0.20	0.40	0.6	0.8	1
v	0	0.05	0.15	0.3	0.5	1

Erläuterung des R-Codes

• einkommen <- c(1000, 2000, 3000, 4000, 10000)

  • Erstellt einen Vektor einkommen, der die Einkommen von 5 Haushalten speichert.

  • Die Werte sind aufsteigend sortiert, was für die Lorenzkurve wichtig ist.

  • Sind die Werte noch nicht sortiert, nutze sort().

• n <- length(einkommen)

  • Dies zählt die Anzahl der Elemente im Vektor (hier n = 5).

• u <- (0:n)

  • Erstellt den Vektor u, der die kumulierten Anteile der Haushalte darstellt.

  • 0:n erzeugt eine Zahlenreihe von 0 bis n (also 0, 1, 2, 3, 4, 5).

  • Durch Teilen durch n wird das Ganze in ein Zahl zwischen 0 und 1t umgewandelt: u = (0, 0.2, 0.4, 0.6, 0.8, 1).

• ant.eink <- einkommen / sum(einkommen)

  • sum(einkommen) berechnet das gesamte Einkommen (1000 + 2000 + 3000 + 4000 + 10000 = 20000).

  • Jedes Einkommen wird durch diese Summe geteilt. Dies ergibt den prozentualen Anteil jedes Haushalts am Gesamteinkommen.

• v <- c(0, cumsum(f))

  • cumsum(f) berechnet die kumulierte Summe der Anteile

  • c(0, ...) setzt am Anfang eine 0, damit die Lorenzkurve immer bei (0,0) beginnt. Für den Vektor u haben wir die Null oben auch schon erzeugt.

  • Ergebnis: v = (0, 0.05, 0.15, 0.3, 0.5, 1)

• rbind(u,v)

  • Dies erzeugt eine Matrix, in der die beiden Vektoren untereinander stehen.

  • So kann man beide Werte direkt nebeneinander sehen.

• plot(u, v, type="l", xlim=c(0,1), ylim=c(0,1), xaxs="i", yaxs="i", col="blue", main="Lorenzkurve")

  • plot(u, v, type="l") zeichnet eine Linie (type="l") basierend auf den u- und v-Werten.

  • xlim=c(0,1), ylim=c(0,1) begrenzen die Achsen exakt auf das Intervall \([0,1]\).

  • xaxs="i", yaxs="i" entfernt extra Platz an den Rändern.

  • col="blue" zeichnet die Lorenzkurve in blau.

  • main="Lorenzkurve" legt den Titel der Grafik fest

• grid()

  • Fügt ein Hintergrund-Gitter hinzu, um die Werte leichter abzulesen.

• points(u, v, pch=16, col="blue")

  • setzt blaue Punkte an die Stützstellen der Lorenzkurve.

  • pch=16 bedeutet gefüllte Kreise.

• abline(0,1, col="red")

  • zeichnet die Diagonale von (0,0) nach (1,1).

  • Diese Linie stellt die perfekte Gleichverteilung dar – alle Haushalte hätten den gleichen Anteil am Einkommen.

  • col="red" macht die Linie rot zur besseren Sichtbarkeit.

Bemerkungen zur Lorenzkurve

• In einem Punkt der Lorenzkurve wird dargestellt, welchen Markanteil die kleinsten Marktteilnehmer für sich beanspruchen. Wird z.B. der Punkt \((0.4,0.15)\) in der Kurve abgetragen, so heißt dies: Die \(40\%\) kleinsten Marktteilnehmer besitzen zusammen \(15\%\) des gesamten Marktanteils.

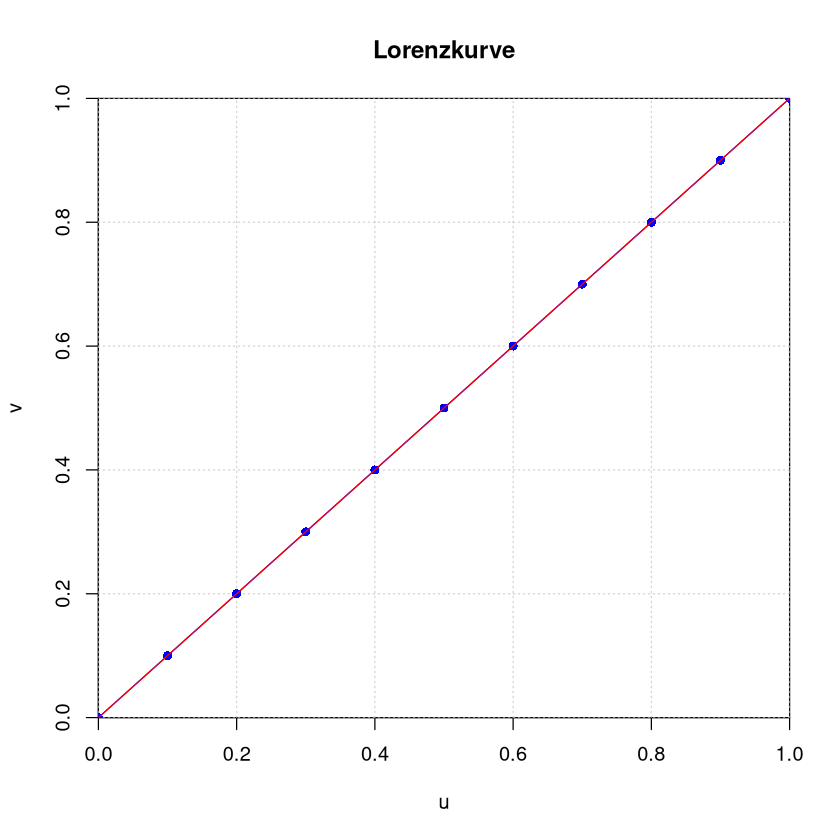
• Die Lorenzkurve liegt genau dann auf der Diagonalen (d.h. auf der Geraden \(u=v\)), wenn der gesamte Markt gleichmäßig unter den Teilnehmener aufgeteilt ist.

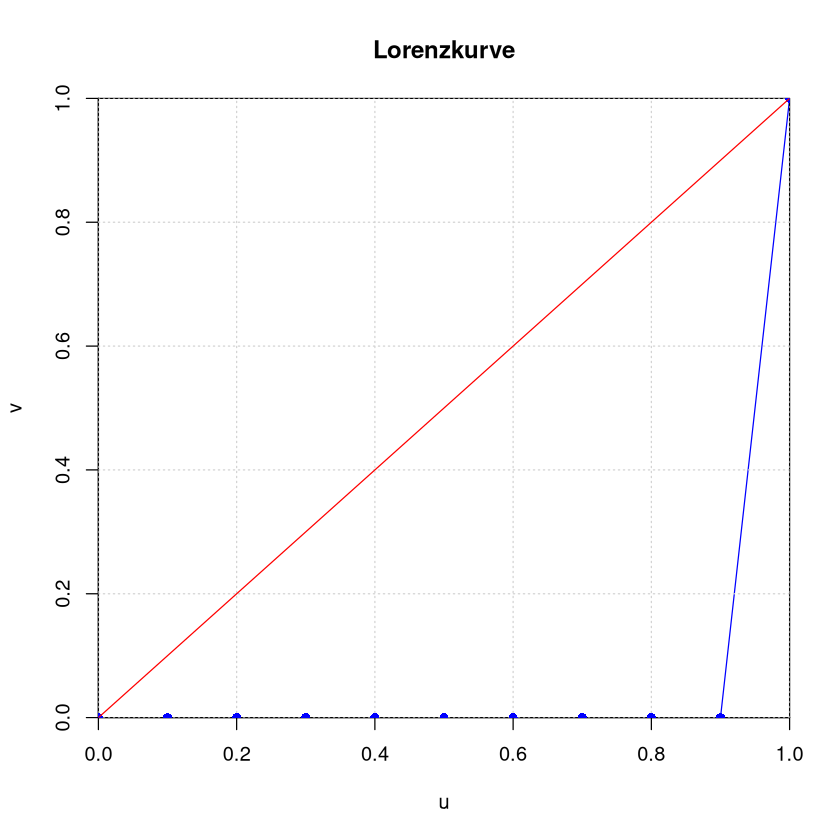
• Je weiter sich die Lorenzkurve „in die Ecke schmiegt“, desto stärker ist die Konzentration der Marktanteile bei wenigen Marktteilnehmern (d.h. desto ungleichmäßiger sind die Anteile verteilt).

• Um die Stärke der Konzentration zu quantifizieren, berechnen wir die Fläche zwischen der Lorenzkurve und der Diagonalen. Dies führt zum Gini-Koeffizient, siehe nächstes Kapitel.

  • große Fläche \(\Rightarrow\) starke Konzentration

  • kleine Fläche \(\Rightarrow\) geringe Konzentration

Gini-Koeffizient

Definition

Ist die geordnete Stichprobe \(x_{1}, \dots ,x_{n}\) gegeben, so gilt berechnet sich der Gini-Koeffizient mittels:

\[ G=\frac{2\sum_{i=1}^n i\cdot x_{i}}{n\sum_{i=1}^{n} x_{i}} - \frac{n+1}{n} \]

Der Gini-Koeffizient entspricht genau dem Verhältznis zwischen Fläche zwischen Diagonale und Lorenzkurve und Fläche zwischen Diagonale und \(u\)-Achse, also

\[\begin{split}\begin{align*} G &= \frac{\text{Fläche zwischen Diagonale und Lorenzkurve}}{\text{Fläche zwischen Diagonale und $u$-Achse}} \\ &= 2 \cdot \text{Fläche zwischen Diagonale und Lorenzkurve}. \end{align*} \end{split}\]

Häufigkeiten

Ist die Stichprobe mit Häufigkeiten gegeben, so gibt es (ähnlich wie bei Mittelwert und Standardabweichung) eine effizientere Methode den Gini-Koeffizient zu berechnen:

Sind die geordneten Ausprägungen \(a_1<\dots< a_k\) und die zugehörigen Häufigkeiten \(h_1,\dots,h_k\) gegeben:

\[ G=\frac{\sum_{i=1}^k (u_{i-1}+u_i)h_i a_i}{\sum_{i=1}^k h_i a_i} - 1 \]

wobei

\[ u_i=\frac1n \sum_{j=1}^i h_j \quad\text{und}\quad v_i=\frac{\sum_{j=1}^i h_ja_j}{\sum_{j=1}^k h_j a_j}\]

Bemerkungen zum Gini-Koeffizient

• Gilt \(x_1=\dots=x_n\), so ergibt sich \(G=0\) (Nullkonzentration)

• Gilt \(x_1=\dots=x_{n-1}=0\) und \(x_n\neq 0\), so gilt \(G=\frac{n-1}{n}\) (maximale Konzentration)

• Folgerung: es gilt immer \(0\leq G \leq \frac{n-1}{n}\)

• Damit der Gini-Koeffizient bei maximaler Konzentration den Wert 1 annimmt, verwendet man gern den normierten Gini-Koeffizient

Definition

Der normierte Gini-Koeffizient ergibt sich mittls

\[G^*= \frac{n}{n-1} G.\]

• Folgerung: es gilt immer \(0\leq G^* \leq 1\)

• Beachte: Es kann trotz gleichem Gini-Koeffizient eine unterschiedliche Verteilung der Anteile vorliegen.

Umsetzung in R

stichprobe <- c(4,2,5,9,1,3,3,4)
x          <- sort(stichprobe)
n          <- length(stichprobe)
G          <- ( 2*sum(x * (1:n)) ) / ( n * sum(x)   )  -  (n+1)/n
Gnorm      <- G * n / (n-1)

cat("Gini-Koeffizient: ",G,"\n\n")

cat("normierter Gini-Koeffizient: ",Gnorm,"\n\n")

Gini-Koeffizient:  0.3024194 

normierter Gini-Koeffizient:  0.3456221 

Herfindahl-Index

In diesem Kapitel folgt eine weitere Methode um die Konzentration zu messen

Wir stellen uns hier vor die Daten liegen in Form einer Liste

\[x_1, x_2, \dots , x_n\]

bestehend aus nicht-negativen Werten vor. Der relative Anteil den ein Wert am Gesamten hat ist \(f_i:=\frac{x_i}{x_1+\dots+x_n}\), \(i=1,\dots,n\) also

\[ f_1:=\frac{x_1}{x_1+\dots+x_n}, f_2:=\quad\frac{x_2}{x_1+\dots+x_n} , \quad \dots\quad, f_n:=\frac{x_n}{x_1+\dots+x_n}.\]

Definition

Der Herfindahl-Index ist nun definiert als die folgende Quadratsumme der relativen Anteile

\[ H:= \sum_{i=1}^{n} f_i^2 \]

Beispiel

In einem fiktiven Land gibt es 5 Städte mit folgenden Einwohnerzahlen

Stadt	\(\text{A}\)	\(\text{B}\)	\(\text{C}\)	\(\text{D}\)	\(\text{E}\)
Einwohnerzahl	\(5000\)	\(15000\)	\(10000\)	\(20000\)	\(50000\)

Die Gesamteinwohnerzahl ist damit

\[G = 5000+15000+10000+20000+50000 = 100000\]

So berechnen sich die Anteil, also die relativen Häufigkeiten mittels

\[f_1=\frac{5000}{100000}=0.05, \quad f_2=0.15,\quad f_3=0.1,\quad f_4=0.2, \quad f_5=0.5\]

und der Herfindahl-Index

\[ H=0.05^2 + 0.15^2 + 0.1^2 + 0.2^2+ 0.5^2 = 0.325\]

• Der Herfindahl-Index liegt bei \(1/n\), wenn \(x_1=\dots=x_n\) also alle Teilnehmer den gleichen Marktanteil haben.

• Der Herfindahl-Index liegt bei \(1\), wenn es einen Marktteilnehmer gibt, der einen 100%igen Marktanteil hat, d.h wenn \(x_1=\dots=x_{n-1}=0\) und \(x_n\neq 0\).

• Im Allgemeinen gilt: \(\frac1n \leq H \leq 1\)

• Je höher der Herfindahl-Index, desto stärker ist die Konzentration

Umsetzung in R

einwohner <- c(5000,15000,10000,20000,50000)
f         <- einwohner/sum(einwohner)
H         <- sum(f^2)
cat("Herfindahl-Index: ",H)

Herfindahl-Index:  0.325

Mehr Beispiele

Wir schauen uns hier noch ein paar Beispiele an.

Beispiel: Monopol

Ein Marktteilnehmer hat alles, alle anderen haben nichts.

x     <- c(0,0,0,0,0,0,0,0,0,1)
n     <- length(x)
# Gini-Koeffizient
G     <- ( 2*sum(x * (1:n)) ) / ( n * sum(x)   )  -  (n+1)/n
# normierter Gini-Koeffizient
Gnorm <- G * n / (n-1)
# Herfindahl-Index
H     <- sum( (x/sum(x))^2 )


cat("Gini-Koeffizient: ",G,"\n\n")

cat("normierter Gini-Koeffizient: ",Gnorm,"\n\n")

cat("Herfindahl-Index: ",H,"\n\n")

u         <- (0:n)/n                          # u-Vektor
f         <- x/sum(x)
v         <- c(0,cumsum(f))                   # kummulierter Anteil der Gesamtsumme
rbind(u,v)                                    # klebt u und v zu Matrix zusammen

# Plot-Befehle:
plot(u,v, type="l", xlim=c(0,1), ylim=c(0,1), xaxs="i", yaxs="i", col="blue", main="Lorenzkurve") # Lorenzkurve
grid()                                        # Gitter
points(u, v, pch=16, col="blue")              # Punkte an den Knicken hinzufügen
abline(0,1, col="red")                        # Diagonale

Gini-Koeffizient:  0.9 

normierter Gini-Koeffizient:  1 

Herfindahl-Index:  1 

A matrix: 2 × 11 of type dbl

u	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
v	0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	1

Beispiel: Nullkonzentration

Alle Marktteilnehmer haben den gleichen Anteil am Markt.

x     <- c(5,5,5,5,5,5,5,5,5,5)
n     <- length(x)
# Gini-Koeffizient
G     <- ( 2*sum(x * (1:n)) ) / ( n * sum(x)   )  -  (n+1)/n
# normierter Gini-Koeffizient
Gnorm <- G * n / (n-1)
# Herfindahl-Index
H     <- sum( (x/sum(x))^2 )


cat("Gini-Koeffizient: ",G,"\n\n")

cat("normierter Gini-Koeffizient: ",Gnorm,"\n\n")

cat("Herfindahl-Index: ",H,"\n\n")

u         <- (0:n)/n                          # u-Vektor
f         <- x/sum(x)
v         <- c(0,cumsum(f))                   # kummulierter Anteil der Gesamtsumme
rbind(u,v)                                    # klebt u und v zu Matrix zusammen

# Plot-Befehle:
plot(u,v, type="l", xlim=c(0,1), ylim=c(0,1), xaxs="i", yaxs="i", col="blue", main="Lorenzkurve") # Lorenzkurve
grid()                                        # Gitter
points(u, v, pch=16, col="blue")              # Punkte an den Knicken hinzufügen
abline(0,1, col="red")                        # Diagonale

Gini-Koeffizient:  0 

normierter Gini-Koeffizient:  0 

Herfindahl-Index:  0.1 

A matrix: 2 × 11 of type dbl

u	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
v	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1

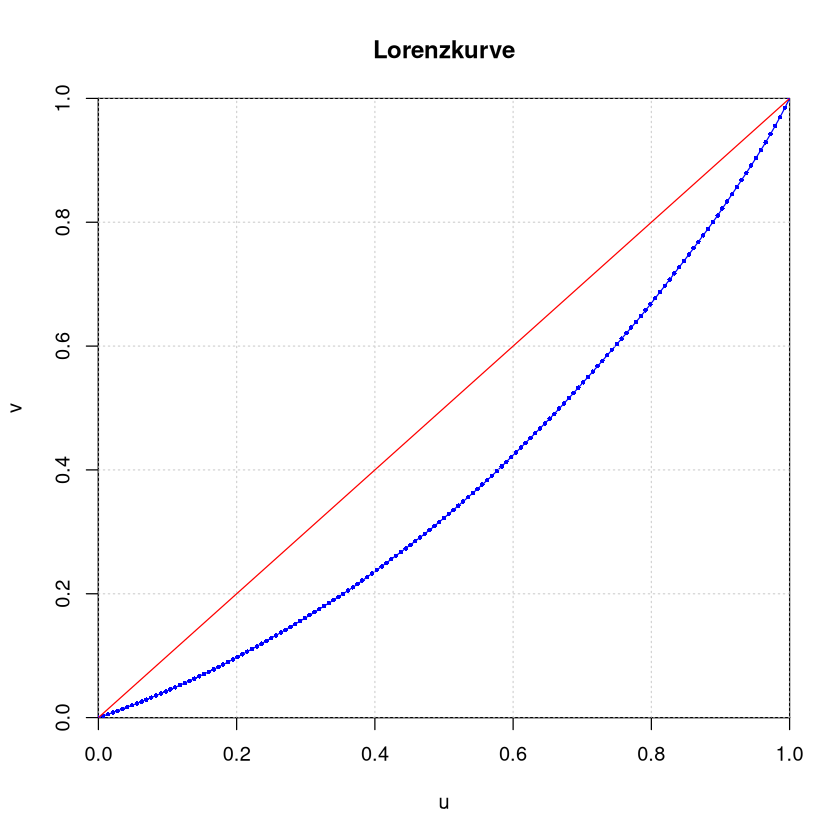
Beispiel: Mittlere Konzentration, reale Daten

Monatliche Passagierzahlen für internationale Flüge von 1949 bis 1960. Mehr Informationen dazu mit der Eingabe help(AirPassengers) in R.

x <- sort(as.numeric(AirPassengers))
cat("Die sortieren Daten: ")
x
n     <- length(x)
# Gini-Koeffizient
G     <- ( 2*sum(x * (1:n)) ) / ( n * sum(x)   )  -  (n+1)/n
# normierter Gini-Koeffizient
Gnorm <- G * n / (n-1)
# Herfindahl-Index
H     <- sum( (x/sum(x))^2 )


cat("Gini-Koeffizient: ",G,"\n\n")

cat("normierter Gini-Koeffizient: ",Gnorm,"\n\n")

cat("Herfindahl-Index: ",H,"\n\n")

u         <- (0:n)/n                          # u-Vektor
f         <- x/sum(x)
v         <- c(0,cumsum(f))                   # kummulierter Anteil der Gesamtsumme
rbind(u,v)                                    # klebt u und v zu Matrix zusammen


# Plot-Befehle:
plot(u,v, type="l", xlim=c(0,1), ylim=c(0,1), xaxs="i", yaxs="i", col="blue", main="Lorenzkurve") # Lorenzkurve
grid()                                        # Gitter
points(u, v, pch=16, col="blue", cex=0.5)     # Punkte an den Knicken hinzufügen
abline(0,1, col="red")                        # Diagonale

Die sortieren Daten: 

1. 104
2. 112
3. 114
4. 115
5. 118
6. 118
7. 119
8. 121
9. 125
10. 126
11. 129
12. 132
13. 133
14. 135
15. 135
16. 136
17. 140
18. 141
19. 145
20. 146
21. 148
22. 148
23. 149
24. 150
25. 158
26. 162
27. 163
28. 166
29. 170
30. 170
31. 171
32. 172
33. 172
34. 178
35. 178
36. 180
37. 180
38. 181
39. 183
40. 184
41. 188
42. 191
43. 193
44. 194
45. 196
46. 196
47. 199
48. 199
49. 201
50. 203
51. 204
52. 209
53. 211
54. 218
55. 227
56. 229
57. 229
58. 229
59. 230
60. 233
61. 234
62. 235
63. 235
64. 236
65. 237
66. 237
67. 242
68. 242
69. 243
70. 259
71. 264
72. 264
73. 267
74. 269
75. 270
76. 271
77. 272
78. 274
79. 277
80. 278
81. 284
82. 293
83. 301
84. 302
85. 305
86. 306
87. 306
88. 310
89. 312
90. 313
91. 315
92. 315
93. 317
94. 318
95. 318
96. 336
97. 337
98. 340
99. 342
100. 347
101. 347
102. 348
103. 348
104. 355
105. 355
106. 356
107. 359
108. 360
109. 362
110. 362
111. 363
112. 364
113. 374
114. 390
115. 391
116. 396
117. 404
118. 404
119. 405
120. 405
121. 406
122. 407
123. 413
124. 417
125. 419
126. 420
127. 422
128. 432
129. 435
130. 461
131. 461
132. 463
133. 465
134. 467
135. 472
136. 472
137. 491
138. 505
139. 508
140. 535
141. 548
142. 559
143. 606
144. 622

Gini-Koeffizient:  0.2407563 

normierter Gini-Koeffizient:  0.2424399 

Herfindahl-Index:  0.00820769 

A matrix: 2 × 145 of type dbl

u	0	0.006944444	0.013888889	0.020833333	0.02777778	0.03472222	0.04166667	0.04861111	0.05555556	0.06250000	⋯	0.9375000	0.9444444	0.9513889	0.9583333	0.9652778	0.9722222	0.9791667	0.9861111	0.9930556	1
v	0	0.002576617	0.005351436	0.008175805	0.01102495	0.01394842	0.01687189	0.01982013	0.02281793	0.02591482	⋯	0.8799395	0.8916334	0.9037980	0.9163095	0.9288953	0.9421500	0.9557268	0.9695761	0.9845898	1