Zwei metrische Merkmale#
Werden 2 Merkmale abgefragt, so sieht eine Stichprobe der Größe \(n\) folgendermaßen aus:
Der erste Eintrag gehört jeweils zum Merkmal \(X\), der zweite zum Merkmal \(Y\).
In diesem Kapitel sollen die beteiligten Merkmale beide metrisch messbar sein. Wir stellen uns zum Beispiel Körpergröße und Körpergewicht vor.
Streudiagramm#
Der erste Schritt ist die graphische Veranschaulichung der Daten. Wir tragen dazu die Punkte in einem 2-dimensionalen Koordiantensystem ab.
# Streudiagram für den cars Datensatz
# cars enthält einen 2-dim. Datensatz.
# Es wurd jeweils die Ausgangsgeschwindigkeit (in mph)
# und der Bremsweg (in ft) gemessen.
# Jede Messung entspricht einem Punkt
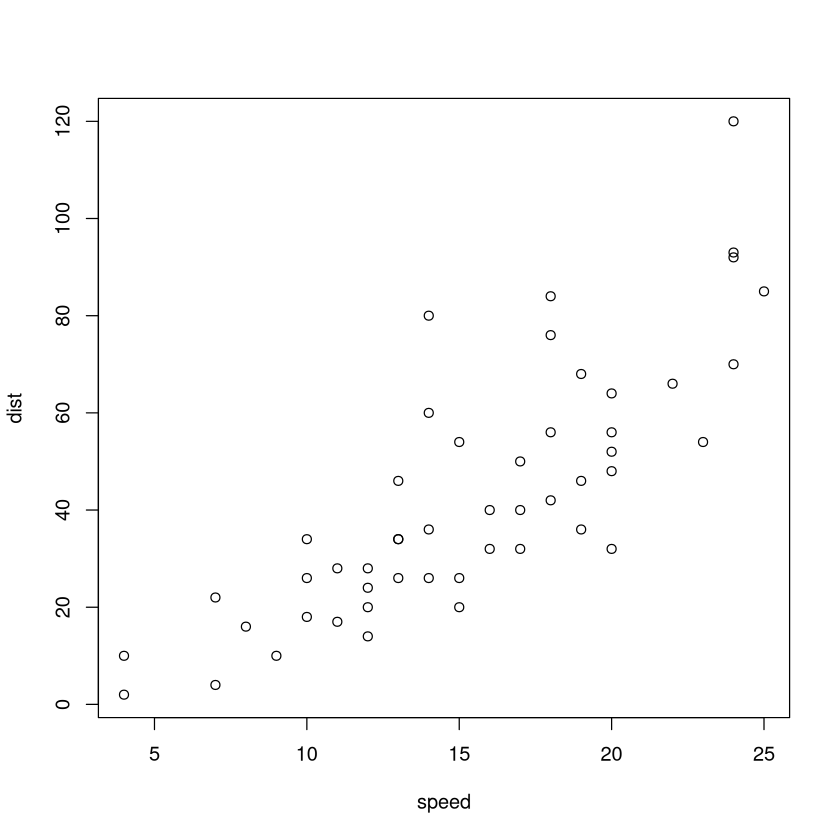
plot(cars)
Wir erkennen im Streudiagramm, dass mit größerer Geschwindigkeit typischerweise auch ein größerer Bremsweg einher geht.
Warnung
Eine Kontingenztafel ist für diese Daten nicht besonders sinnvoll, da zu viele verschieden Ausprägungen vorliegen. Ein Ausweg könnte sein die Daten zu klassieren und sie dann wie ordinale oder nominale Merkmale zu behandeln.
Wir können die beiden Stichproben auch getrennt voneinander oder nebeneinander betrachten und über 2 Boxplots oder 2 Verteilungsfunktionen darstellen. Dabei verlieren wir allerdings den Zusammenhang zwischen beiden Größen.
Ein wichtige Fragen beim Analysieren eines Streudiagramms sind:
Wie stark ähneln die Daten einer Geraden? -> Antwort liefert der Korrelationskoeffizient, siehe unten
Welche Gerade approximiert die Daten am besten? -> Antwort liefert die Regressionsgerade
Maßzahlen#
Wichtige Maßzahlen sind die Stichproben-Kovarianz und der Stichproben-Korrelationskoeffizient. Sie sind wie folgt definiert:
Definition
Ist \((x_1,y_1),\dots,(x_n,y_n)\) die zweidimensionale Stichprobe zweier metrisch messbarer Merkmale \(X\) und \(Y\), so definieren wir
die Stichproben-Kovarianz mittels
\[ s_{x,y} = \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar x) (y_i - \bar y) \]den Stichproben-Korrelationkoeffizient mittels
\[ r_{x,y} = \frac{s_{x,y}}{s_x\cdot s_y}\]
wobei
Setzt man alles ein und kürzt, so ergibt sich:
Berechnung in R:#
Man nutz nur die Befehle cov() für die Stichprobenkovarianz und cor() für die den Stichprobenkorrelationskoeffizient.
Die hier definierten Maßzahlen quantifizieren die Stärke des linearen Zusammenhangs. Grob gesagt geben sie Auskunft darüber wie sehr das Streudiagramm einer Geraden ähnelt. Der Korrelationskoeffizient ist die normierte Version der Kovarianz. Während die Kovarianz beliebige (positive wie negative) Werte annehmen kann, liegt der Korrelationskoeffizient immer im Intervall \([-1,1]\).
Je näher \(r_{x,y}\) an \(1\) oder \(-1\) liegt, desto mehr ähnelt das Streudiagramm einer Geraden.
Ein positiver Korrelationskoeffizient sagt, dass
große \(x\)-Werte typischerweise mit großen \(y\)-Werten zusammenfallen.
kleine \(x\)-Werte typischerweise mit kleinen \(y\)-Werte zusammenfallen.
Ein negativer Korrelationskoeffizient sagt, dass
große \(x\)-Werte typischerweise mit kleinen \(y\)-Werten zusammenfallen.
kleine \(x\)-Werte typischerweise mit großen \(y\)-Werte zusammenfallen.
Gilt \(r_{x,y}=1\), so liegen alle Punkte auf einer steigenden Gerade.
Gilt \(r_{x,y}=-1\), so liegen alle Punkte auf einer fallenden Gerade.
Gilt \(r_{x,y}=0\) so ist liegt kein linearer Zusammenhang vor.
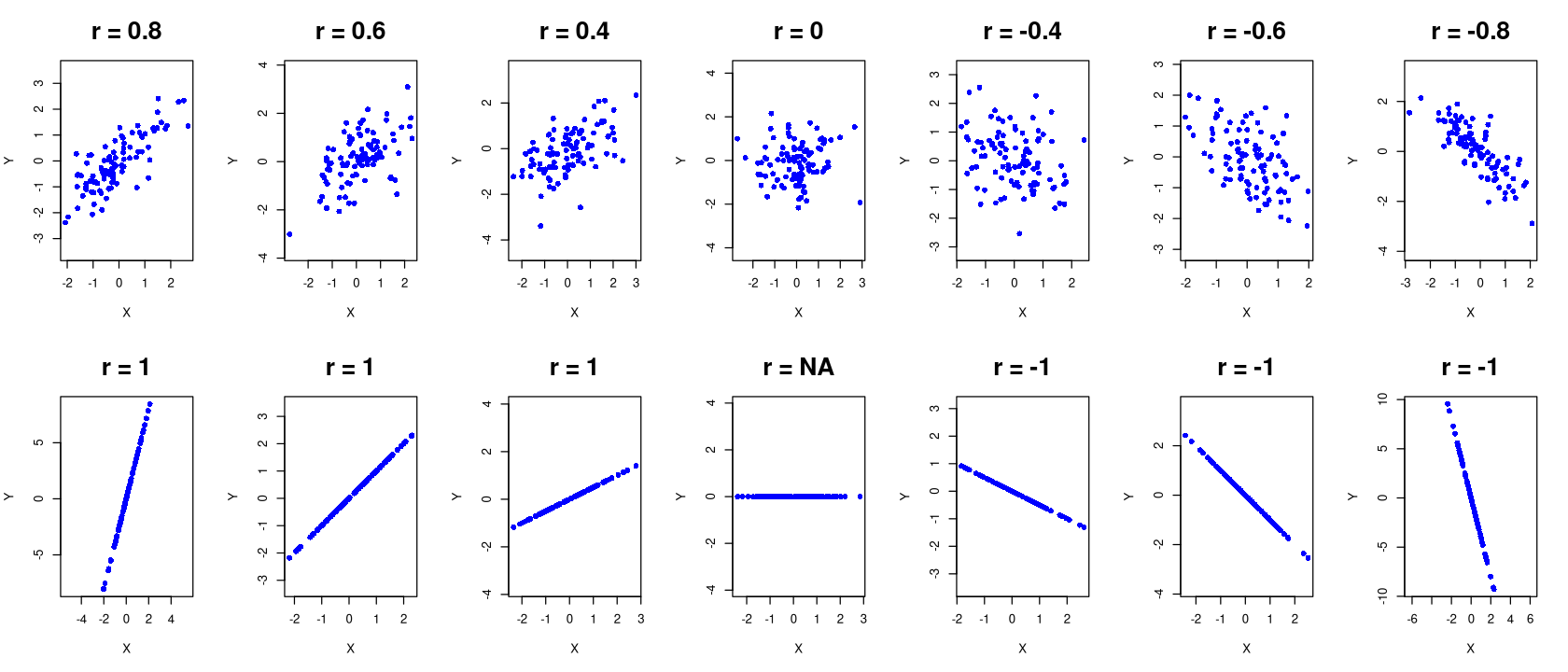
Die folgende Grafik zeigt Streudiagramme und zugehörige Korrelationskoeffizienten.
cov(cars$dist,cars$speed)
cor(cars$dist,cars$speed)
Interpretation#
Die hier definierten Maßzahlen quantifizieren die Stärke des linearen Zusammenhangs. Grob gesagt geben sie Auskunft darüber wie sehr das Streudiagramm einer Geraden ähnelt. Der Korrelationskoeffizient ist die normierte Version der Kovarianz. Während die Kovarianz beliebige (positive wie negative) Werte annehmen kann, liegt der Korrelationskoeffizient immer im Intervall \([-1,1]\).
Je näher \(r_{x,y}\) an \(1\) oder \(-1\) liegt, desto mehr ähnelt das Streudiagramm einer Geraden.
Ein positiver Korrelationskoeffizient sagt, dass
große \(x\)-Werte typischerweise mit großen \(y\)-Werten zusammenfallen.
kleine \(x\)-Werte typischerweise mit kleinen \(y\)-Werte zusammenfallen.
Ein negativer Korrelationskoeffizient sagt, dass
große \(x\)-Werte typischerweise mit kleinen \(y\)-Werten zusammenfallen.
kleine \(x\)-Werte typischerweise mit großen \(y\)-Werte zusammenfallen.
Gilt \(r_{x,y}=1\), so liegen alle Punkte auf einer steigenden Gerade.
Gilt \(r_{x,y}=-1\), so liegen alle Punkte auf einer fallenden Gerade.
Gilt \(r_{x,y}=0\) so ist liegt kein linearer Zusammenhang vor.
Die folgende Grafik zeigt Streudiagramme und zugehörige Korrelationskoeffizienten.
Show code cell source
# Notwendiges Paket laden
library(MASS)
options(repr.plot.width = 14, repr.plot.height = 6)
# Anzahl der Punkte
n <- 100
# Mittelwerte der beiden Variablen
mu <- c(0, 0)
rvec <- c(0.8,0.6,0.4,0,-0.4,-0.6,-0.8)
par(mfrow = c(2, 7)) # Layout mit 3 Zeilen und 7 Spalten
set.seed(1234)
for (i in 1:7) {
r <- rvec[i]
Sigma <- matrix(c(1, r, r, 1), ncol=2)
data <- mvrnorm(n, mu, Sigma)
# Erstellen einer Punktwolke
plot(data, main=paste("r =", r), cex.main=2,
xlab="X", ylab="Y", pch=16, col="blue",asp=1)
}
mvec <- c(4,1,0.5,0,-0.5,-1,-4)
rvec <- c(1,1,1,"NA",-1,-1,-1)
for (i in 1:7) {
sig <- 0.5
r <- rvec[i]
x <- rnorm(100,mean = 0,sd = 1)
y <- mvec[i]*x
data <- mvrnorm(n, mu, Sigma)
# Erstellen einer Punktwolke
plot(x,y, main=paste("r =", r), cex.main=2,
xlab="X", ylab="Y", pch=16, col="blue", asp=1)
}
par(mfrow = c(1, 1)) # Zurücksetzen
Warnung
Der Korrelationskoeffizient kann nur einen linearen Zusammenhang messen. Es folgen ein paar Beispiele, in denen jeweils offensichtlich ein deutlicher Zusammenhang zwischen \(x\) und \(y\) vorliegt, aber immer \(r_{x,y}\approx 0\) gilt.
Show code cell source
par(mfrow = c(2, 2)) # Layout mit 2 Zeilen und 3 Spalten
options(repr.plot.width = 10, repr.plot.height = 10)
set.seed(232) # Reproduzierbarkeit
n <- 200
## Grafik 1##
# Erzeuge Punkte auf einem Kreis mit zufälligem Winkel
theta <- runif(n, 0, 2 * pi) # Gleichverteilte Winkel
x <- cos(theta)
y <- sin(theta)
# Streudiagramm zeichnen
plot(x, y, main = paste("Korrelation:", round(cor(x, y), 3)),
xlab = "x", ylab = "y", pch = 16, col = "blue", asp=1)
## Grafik 2 ##
x <- runif(n, -2*pi, 2 * pi) # Gleichverteilte Winkel
e <- runif(n,min = -0.4,max=0.4)
y <- 2*cos(x)+e
# Streudiagramm zeichnen
plot(x, y, main = paste("Korrelation:", round(cor(x, y), 3)),
xlab = "x", ylab = "y", pch = 16, col = "blue", asp=1)
## Grafik 3 ##
x <- runif(n, -2*pi, 2 * pi) # Gleichverteilte Winkel
e <- runif(n,min = -0.6,max=0.6)
y <- 0.18*x^2+e
# Streudiagramm zeichnen
plot(x, y, main = paste("Korrelation:", round(cor(x, y), 3)),
xlab = "x", ylab = "y", pch = 16, col = "blue", asp=1)
## Grafik 4 ##
theta <- runif(n, 0, 2 * pi) # Gleichverteilte Winkel
r <- runif(n, min = 0,max=0.4)
x <- r*cos(theta) + sample(c(-1,1),n,replace = T)
y <- r*sin(theta) + sample(c(-1,1),n,replace = T)
# Streudiagramm zeichnen
plot(x, y, main = paste("Korrelation:", round(cor(x, y), 3)),
xlab = "x", ylab = "y", pch = 16, col = "blue", asp=1)
Klassierung#
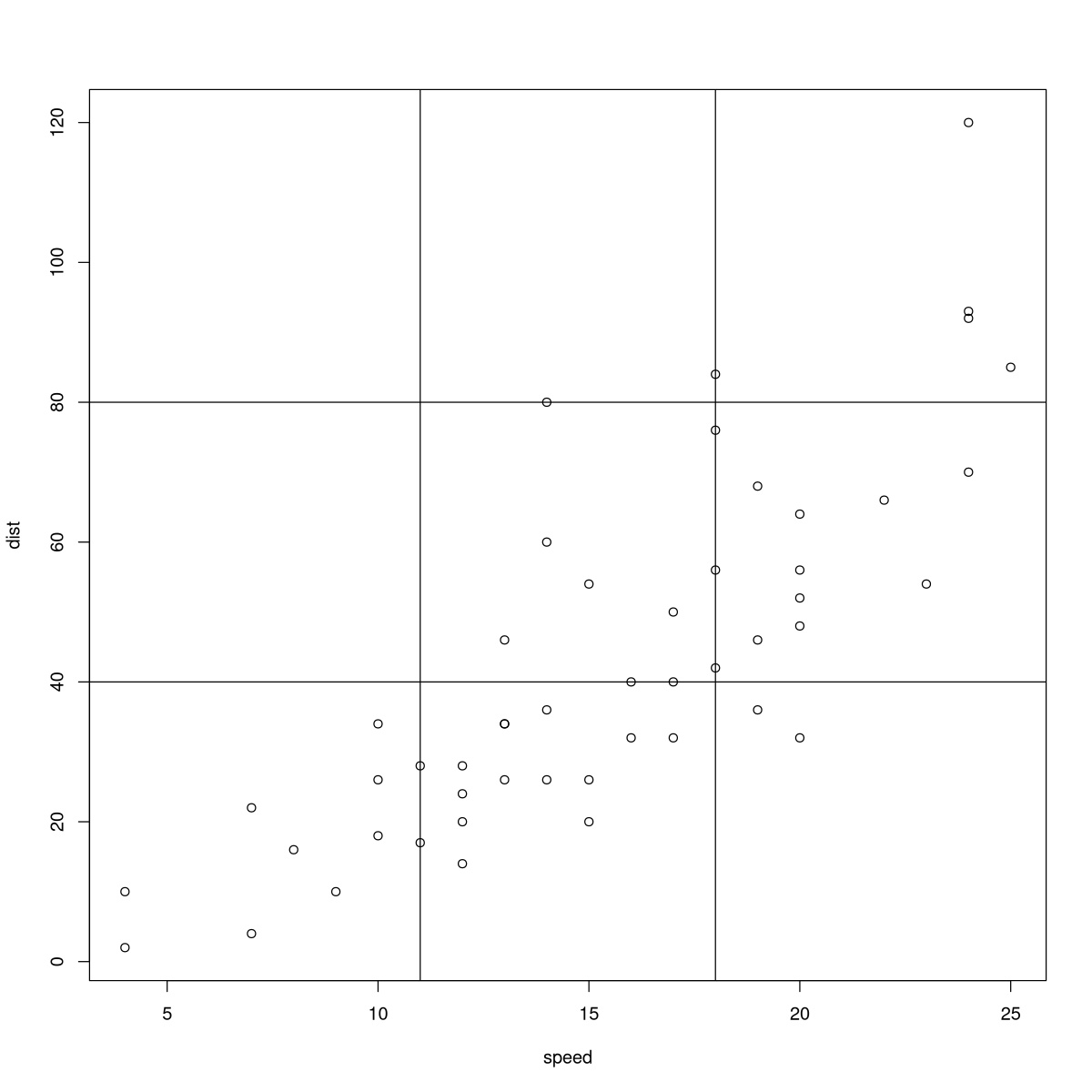
Durch Klassierung der Daten lässt sich wieder ein Merkmal mit wenigen Ausprägungen erzeugen. Auf diese Weise können andere Methoden wie Kontingenztafeln, Säulendiagramme usw. zur Veranschaulichung der Daten angewandt werden.
plot(cars)
abline(v=11)
abline(v=18)
abline(h=40)
abline(h=80)
cat("Kontingenztafel für die klassierten Daten:")
table(cut(cars$dist, breaks =c(0,40,80,120) ),
cut(cars$speed, breaks = c(3,11,18,25) )
)