Grundlagen#
Was ist eine stetige Zufallsvariable?#
Im Kapitel Grundlagen zu Zufallsvariablen haben wir bereits gelernt, was eine Zufallsvariable ist. Im Beispiel zu Wartezeiten ist uns auch schon eine stetige Zufallsvariable begegnet.
Um genau zu definieren was eine stetige Zufallsvariable ist, erinnern wir uns noch an die Definition der Verteilungsfunktion, aus dem Kapitel Verteilungsfunktion: Ist \(X\) eine Zufallsvariable, so ist die Verteilungsfunktion \(F_X\) oder \(F\) gegeben durch:
Die Definition einer stetigen Zufallsvariable lautet dann:
Definition
Eine Zufallsvariable \(X\) heißt stetige Zufallsvariable, falls die zugehörige Verteilungsfunktion \(F_X\) stetig ist.
Ist \(F_X\) nicht nur stetig, sondern sogar differenzierbar, so heißt die Ableitung \(f_X=F_X^`\) Wahrscheinlichkeitsdichte oder Dichtefuntion der Zufallsvariable \(X\)
Für die Begriffe Stetigkeit und Differenzierbarkeit einer Funktion, sei auf Ihre Grundvorlesung verwiesen, siehe auch Stetigkeit Wikipedia und Differenzierbarkeit Wikipedia.
Im Rahmen dieser Vorlesung gehen wir immer davon aus, dass die Verteilungsfunktion \(F_X\) einer stetigen Zufallsvariable auch (bis auf endlich viele Stellen) differenzierbar ist.
Eigenschaften der Wahrscheinlichkeitsdichte
Sei \(X\) eine stetige Zufallsvariable mit Wahrscheinlichkeitsdichte \(f\). Dann gilt
\(f\) ist auf ganz \(\mathbb R\) definiert
\(f(x)\geq 0\) für alle \(x\in \mathbb R\)
\(\int_{-\infty}^\infty f(x) \mathrm d x = 1\)
Der Satz sagt, dass jede Wahrscheinlichkeitsdichte diese 3 Eigenschaften hat. Die Umkehrung gilt auch: jede Funktion \(f\) die diese 3 Eigenschaften hat, ist Wahrscheinlichkeitsdichte einer Zufallsvariable. Die Verteilungsfunktion berechnet man aus der Dichte dann wie folgt:
Merke
Die Verteilung einer stetigen Zufallsvariable gibt man an, indem man
die Wahrscheinlichkeitsdichte
oder
die Verteilungsfunktion angibt.
Unabhängigkeit von stetigen Zufallsvariablen#
Unabhängigkeit von Zufallsvariablen haben wir schon im Zusammenhang mit diskreten Zufallsvariablen kennengelernt. Die Definition von Unabhängigkeit ist für stetige Zufallsvariablen exakt die gleiche. So nennen wir zwei Zufallsvariablen \(X\) und \(Y\) genau dann unabhängig, wenn für alle \(s\) und \(t\) gilt:
Für den Fall mit mehr als 2 Zufallsvariablen, schauen Sie bitte in hier.
Wahrscheinlichkeiten bei stetigen Zufallsvariablen#
Wir lernen hier wie man bei stetigen Zufallsvariablen mit Hilfe von Verteilungsfunktion und Dichtefunktion Wahrscheinlichkeiten berechnet. Entscheidend ist dabei der folgende Zusammenhang:
Wahrscheinlichkeiten - Verteilunungsfunktion - Dichte
Sei \(X\) eine stetige Zufallsvariable mit Verteilungsfunktion \(F\) und Wahrscheinlichkeitsdichte \(f\). Dann gilt
Wahrscheinlichkeit |
mit Verteilungsfunktion |
mit Wahrscheinlichkeitsdichte |
|---|---|---|
\(\mathbb P(X\leq t)=\mathbb P(X<t)\) |
\(=F(t)\) |
\(=\int\limits_{-\infty}^t f(x) \mathrm d x\) |
\(\mathbb P(X\geq t)=\mathbb P(X>t)\) |
\(=1-F(t)\) |
\(=\int\limits_t^{\infty} f(x) \mathrm d x\) |
\(\mathbb P(s\leq X\leq t)=\mathbb P(s<X<t)\) |
\(=F(t)-F(s)\) |
\(=\int\limits_{s}^t f(x) \mathrm d x\) |
Beachte: In den Ereignissen kann man jeweils \(\leq \) durch \(<\) und \(\geq \) durch \(>\) (und andersrum) ersetzen. Zum Beispiel gilt
Wir erkennen, das Wahrscheinlichkeiten berechnet werden, indem die zugehörige Fläche unter der Wahrscheinlichkeitsdichte bestimmt wird. Noch leichter lassen sich Wahrscheinlichkeiten aber mit Hilfe der Verteilungsfunktion berechnen, da hier kein Integrieren mehr notwendig ist.
Verschanschaulichung des Zusammenhangs zwischen „Wahrscheinlichkeiten - Verteilunungsfunktion - Dichte“: (am Beispiel der Normalverteilung)
Beispiele#
Beispiel: Exponentialverteilung (Spezialfall)
Gegeben sei die Wahrscheinlichkeitsdichte
Dann ist die Verteilungsfunktion gegeben durch:
Begründung:
Variante 1: Leite \(F\) ab.
Offensichtlich gilt für \(x\geq 0\): \(F'(x)= \mathrm{e}^{-x}\). Für \(x<0\) ist \(F\) konstant, daher ist dort auch die Ableitung gleich Null. Außerdem liegt \(F\) zwischen \(0\) und \(1\).
Variante 2: Integriere \(f\)
für \(t\geq 0\) gilt: \(\int\limits_{-\infty}^t f(x)\mathrm d x = \int\limits_0^t \mathrm{e}^{-x} \mathrm d x =[-\mathrm{e}^{-x}]_0^t= -\mathrm{e}^{-t}-(-1)= 1- \mathrm{e}^{-t}\)
Wahrscheinlichkeiten berechnen:
\(\mathbb P(X\geq 2)\)
Variante 1: mit \(F\)
\(\mathbb P(X\geq 2)= 1- F(2)= 1-(1-\mathrm{e}^{-2})= \mathrm{e}^{-2}\approx 0.1353 \)
Variante 2: mit \(f\)
\(\mathbb P(X\geq 2)= \int\limits_2^\infty \mathrm{e}^{-x}\mathrm d x = [-\mathrm{e}^{-x}]_2^\infty = - (-\mathrm{e}^{-2})\approx 0.1353 \)
Beispiel
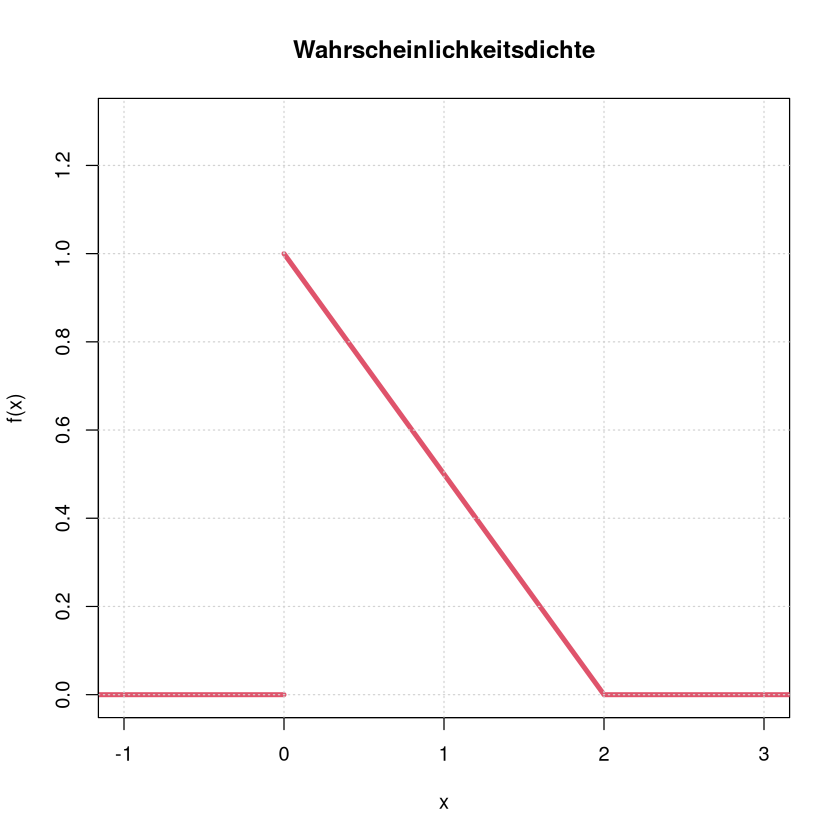
Die Funktion \(f\) gegeben durch
ist eine Wahrscheinlichkeitsdichte.
Begründung:
\(f\) ist auf ganz \(\mathbb R\) definiert
\(f(x)\) ist für alle \(x\) nicht-negativ (siehe Grafik unten)
\(\int_{-\infty}^\infty f(x)\mathrm d x = 1\), denn
\[\int\limits_{-\infty}^\infty f(x)\mathrm d x =\int\limits_{0}^2 1-\frac x2 = [x-\frac{x^2}{4}]_{0}^2 =(2-1)-0=1\]
Die Verteilungsfunktion ist
denn
Wahrscheinlichkeiten berechnen:
Gesucht \(\mathbb P(\frac12< X <1)\).
Nutze die Verteilungsfunktion:
plot(c(-2,0),c(0,0),
xlim=c(-1,3), ylim=c(0,1.3),
type = "l", col=2, lwd=4,
main = "Wahrscheinlichkeitsdichte",
xlab = "x", ylab="f(x)")
points(c(0,2,4),c(1,0,0), type="l", col=2, lwd=4)
grid()
x <- seq(from = 0, to =2,length.out = 50)
y <- x-x^2/4
plot(c(-2,x,4),c(0,y,1),
xlim=c(-1,3), ylim=c(0,1.3),
type="l", col=2, lwd=4,
main = "Verteilungsfunktion",
xlab = "x", ylab="F(x)")
grid()