Maßzahlen für univariate Stichproben

Inhalt

Maßzahlen für univariate Stichproben#

Wir haben bereits Histogramme kennengelernt. Diese zeigen optisch die Verteilung der Stichprobe. Damit ist beispielsweise für metrische Merkmale gemeint, dass die Histogramme verdeutlichen:

wo wieviele Werte der Stichprobe liegen
welches sind die größten und kleinsten Werte
in welchem Bereich liegen besonders viele Werte, wo liegen wenige, wo liegen keine Werte
wie stark streuen die Werte, liegen die Werte alle eng zusammen, liegen die Werte weit auseinander
usw.

Um Dieses und Ähnliches mit Zahlenwerten zu quantifizieren wurden verschiedene Maßzahlen entwickelt. Ein paar besonders wichtige werden wir hier kennenlernen.

Sei von hier an $x_1, \dots , x_n$ eine Stichprobe eines metrischen Merkmals.

Modus#

Der Modus (oder Modalwert) einer Stichprobe ist ein Wert, welcher am häufigsten in der Stichprobe vorkommt.

Beispiel

Eine Umfrage nach der Lieblingsfarbe ergab die Stichprobe

\[\text{lila, rot, lila, gelb, blau, grün, pink, lila} \]

Der Wert lila wurde am häufigsten gewählt, daher ist der Modalwert der Stichprobe: $x_{\text{mod}}= \text{"lila"}$.

In einer weiteren Umfrage wurde die Note in Mathematik abgefragt. Hier ergab sich


Note	1	2	3	4	5	6
Häufigkeit	4	7	7	3	0	1

Hier gibt es daher zwei Modalwerte: 2 und 3.

Arithmetisches Mittel#

Umgangssprachlich auch Mittelwert genannt, berechnet sich wie folgt

\[ \bar x = \frac1n \sum_{i=1}^n x_i \]

Es ist ein sogenanntes Lagemaß, es beschreibt die (mittlere) Lage der Stichprobe auf der reellen Achse.

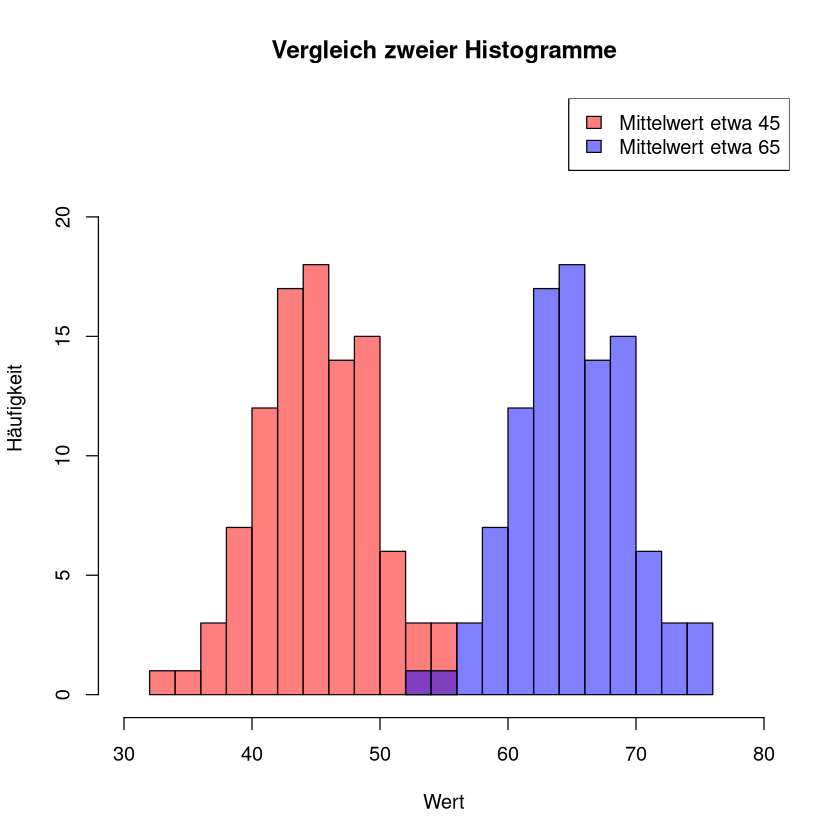
Hier sehen wir zwei Stichproben mit ihren Histogramme dargestellt. Man erkennt, dass die Verteilung der Stichproben gleich ist - bis auf eine Verschiebung um 20. Diese unterschiedliche Lage der Stichprobe wird durch die Unterschiedlichen Mittelwerte verdeutlicht. Die Mittelwerte untescheiden sich auch genau um 20.

../../_images/9ec938b08c154616eb128cc9f28375f8d519a0e839b40bd45186bc15a07375a1.png

Varianz#

Die Varianz misst die Streuung der Stichprobe. Sie gibt an, wie weit die einzelnen Werte im Durchschnitt vom Mittelwert entfernt sind. Eine hohe Varianz zeigt an, dass die Werte weit verstreut sind, während eine niedrige Varianz bedeutet, dass die Werte nahe am Mittelwert liegen.

\[ s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2 \]

In der Formel sieht man, dass die Varianz die mittlere quadratische Abweichung vom Mittelwert misst

Standardabweichung#

Die Standardabweichung einer Stichprobe ist die Wurzel der Varianz:

\[ s = \sqrt{s^2} = \left(\frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2\right)^{\frac12} \]

Ebenso wie die Varianz ist sie ein Maß für die Streuung der Stichprobenwerte um den Mittelwert.

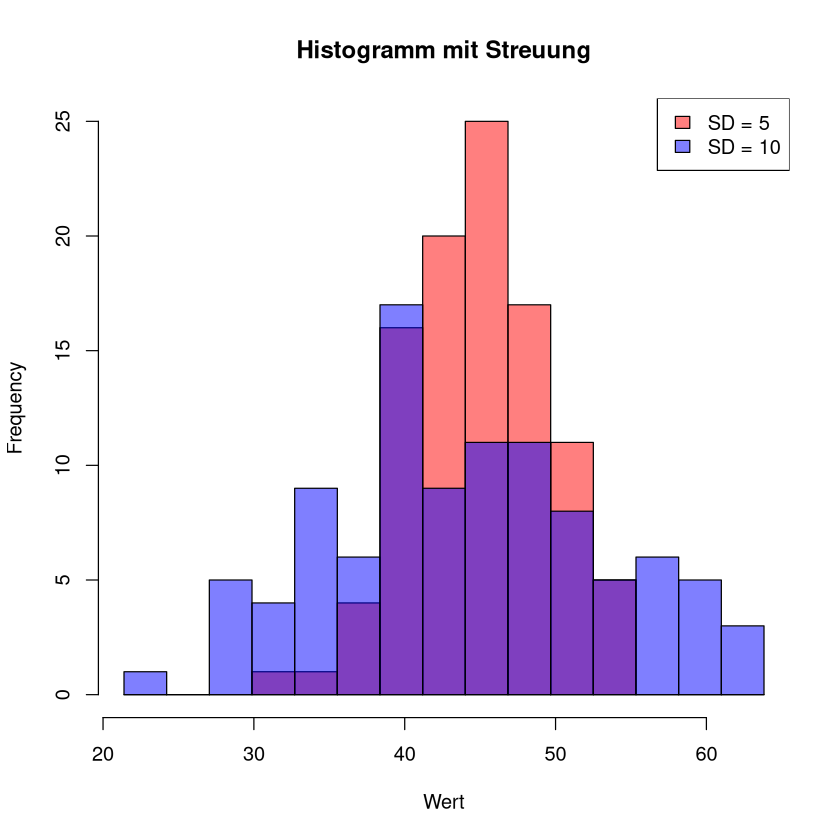
In der folgenden Grafik sieht man 2 Histogramme. Die zugehörigen Stichproben haben den gleichen Mittelwert, jedoch unterschiedliche Varianz bzw. unterscheidliche Standardabweichung (5 und 10). Das Histogramm zur Stichprobe mit der größeren Standardabweichung (blau) ist flacher und breiter als das andere (rot).

../../_images/283ede3b3ce8e152c87de0f3467bfdb525c2b09b9254916972b7615e1bd6e3ce.png

Vergleich von Varianz und Standardabweichung#

Beide Maßzahlen messen die Streuung der Stichprobe, aber sie haben unterschiedliche Einheiten:

Die Einheit der Varianz ist das Quadrat der ursprünglichen Einheit (z.B. $m^2$, wenn die Stichprobe in Meter $m$ angegeben ist). Die Standardabweichung ist in der gleichen Einheit wie die ursprünglichen Daten (z.B. $m$) angegeben. Oft wird die Standardabweichung bevorzugt, da sie etwas leichter zu interpretieren ist. Die Varianz hingegen ist leichter zu berechnen (da keine Wurzel gezogen werden muss).

Beispiel

Stellen Sie sich vor, Sie haben eine Stichprobe von 10 Werten, die wie folgt sind: 10, 12, 15, 16, 20, 22, 25, 28, 30, 32. Die Einheit der Werte sei $g$ (Gramm).

Der Mittelwerte der Stichprobe ist

\[ \bar x =\frac1{10}\sum_{i=1}^{10} x_i = \frac{10+ 12+ 15+ 18+20+ 22+ 25+ 28+ 30+ 32}{10} = 21\]

Mit Einheit: $\bar x = 21 g$

Die Varianz und die Standardabweichung dieser Stichprobe ist dann

\[s^2 = \frac19\sum_{i=1}^{10}(x_i-\bar x)^2 = \frac{(10-21)^2+(12-21)^2+\dots + (30-21)^2}{9} = 59.\bar{1}\]

\[s= \sqrt{59.\bar 1} \approx 7.688 \]

Mit Einheit: $s^2 = 59.\bar{1} g^2$ und $s\approx 7.688 g$

Variationskoeffizient#

Der Variationskoeffizient ist ein relatives Streuungsmaß, das die Standardabweichung in Relation zum Mittelwert setzt. Dadurch wird die Vergleichbarkeit von Streuungen zwischen Datensätzen mit unterschiedlichen Mittelwerten verbessert. Er wird wie folgt berechnet:

\[ v = \frac{s}{\bar{x}} \]

Dabei ist:

$s$ die Standardabweichung der Stichprobe
$\bar{x}$ der Mittelwert der Stichprobe

Der Variationskoeffizient wird genutzt, um die Streuung relativ zum Mittelwert zu bewerten. Besonders hilfreich ist er, wenn man Datensätze mit sehr unterschiedlichen Skalen vergleichen möchte.

Beispiel:

Eine Standardabweichung von 5 kann bei einem Mittelwert von 50 als relativ gering angesehen werden (v = 0.1 = 10%).
Dieselbe Standardabweichung bei einem Mittelwert von 10 wäre jedoch sehr hoch (v = 0.5 = 50%).

Vorteile gegenüber der Standardabweichung und Varianz:

Er ist ein einheitsloses Maß und ermöglicht daher Vergleiche zwischen verschiedenen Datensätzen, unabhängig von der Skalierung.
Besonders nützlich in Wirtschafts- und Sozialwissenschaften, wo absolute Streuungen oft weniger aussagekräftig sind als relative Streuungen.

Nachteile:

Er setzt voraus, dass der Mittelwert $\bar{x} \neq 0$ ist, da eine Division durch Null nicht definiert ist.
Bei Daten mit negativen oder um Null schwankenden Mittelwerten kann er schwer interpretierbar sein.

Spannweite#

Die Spannweite ist ein weiteres Maß zur Qunatifizierung der Streuung einer Stichprobe. Sie ist definiert als Abstand zwischen minimalem und maximalem Wert der Stichprobe:

\[ r = \max(x_1,\dots, x_n) - \min(x_1,\dots, x_n)\]

Da nur größter und kleinster Wert der Stichprobe in die Berechnung eingehen, hat die „Verteilung dazwischen“ keinen Einfluss auf die Spannweite. Beispielsweise haben die beiden Stichproben $$ 0,1,2,3,4,5,6,7,8,9,10 $$ und $$ 0,5,5,5,5,5,5,5,5,5,10 $$ den gleichen Mittelwert und die gleiche Spannweite.

Schiefe#

Die Schiefe ist ein Maß für die Asymmetrie einer Verteilung. Sie gibt an, wie stark die vorliegende Verteilung von einer vollkommen symmetrischen Verteilung abweicht. Die Schiefe kann mit der folgenden Formel berechnet werden:

\[ g_m = \frac{\frac1n \sum_{i=1}^n (x_i - \bar x)^3}{ \left(\frac1n \sum_{i=1}^n(x_i-\bar x)^2 \right)^{\frac32} } \]

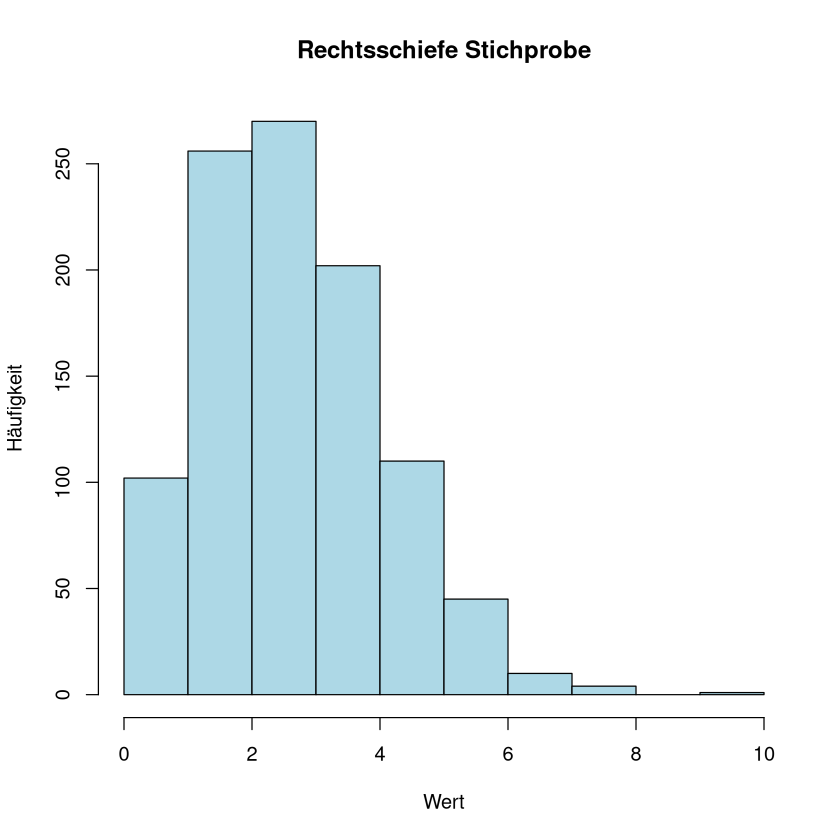
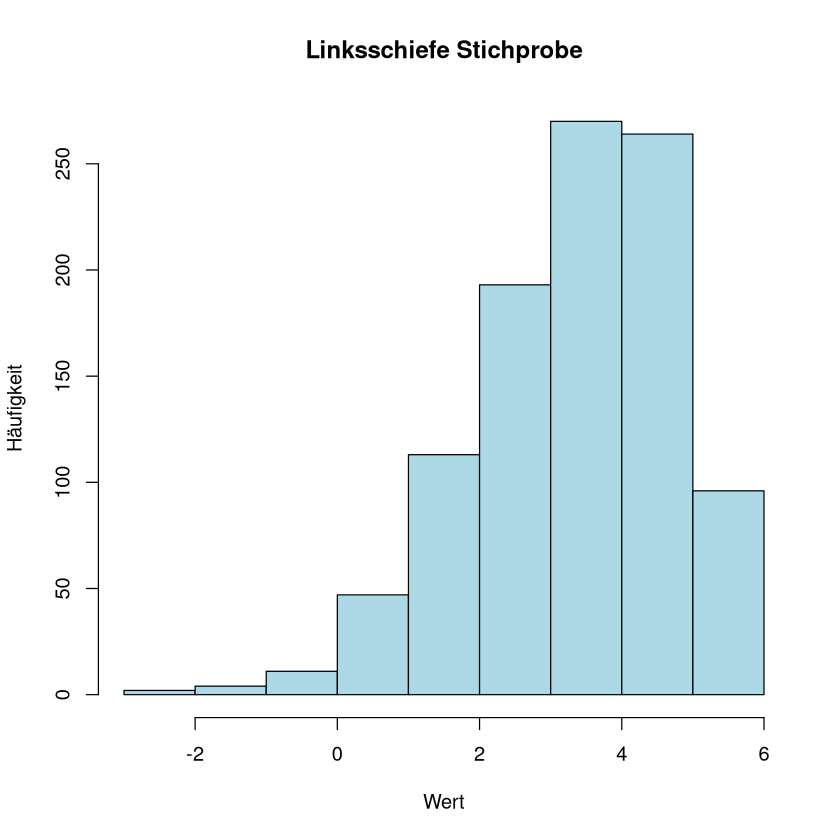
Eine positive Schiefe $g_m>0$ bedeutet, dass die Verteilung rechtsschief ist, d.h. dass die Verteilung länger nach rechts ausläuft als nach links. Eine negative Schiefe $g_m<0$ bedeutet, dass die Verteilung linksschief ist, d.h. dass die Verteilung länger nach links ausläuft als nach rechts. Eine Schiefe von $0$ bedeutet, dass die Verteilung symmetrisch ist, d.h. dass die Verteilung gleichmäßig auf beiden Seiten der Mittelwert verteilt ist.

Vergleich mit anderen Maßzahlen

Die Schiefe kann mit anderen Maßzahlen wie der Varianz und der Standardabweichung verglichen werden. Während die Varianz und die Standardabweichung die Streuung der Stichprobe messen, gibt die Schiefe an, wie asymmetrisch die Verteilung ist.

Im folgenden Beispiel erzeugen wir zufällige Werte, plotten das Histogramm und berechnen dazu die Schiefe

[1] "Schiefe der rechtsschiefen Stichprobe:  0.66"

../../_images/25dfea8d8353535e9d27abdf634f89aa09f821006a43316fe5b08f0e895c5abd.png

[1] "Schiefe der linksschiefen Stichprobe:  -0.65"

../../_images/e66818a0d4f04ed4faad9dd23e2fef17d9d0b3997a761d1674d718672c8afffc.png

Median#

Der Median $m$ bezeichnet die Mitte der Stichprobe. Um ihn zu ermitteln wird die Stichprobe aufsteingend sortiert.

Ist die Stichprobengröße ungerade, so ist $m$ der Wert in der Mitte.
Ist die Stichprobengröße gerade, so ist $m$ der Durchschnitt der beiden mittleren Werte

Beispiel 1 Der Median der Stichprobe $2,5,7,8,9$ ist $m=7$, da es $n=5$ (ungerade) Werte gibt und die 7 in der Mitte der geordneten Stichprobe steht.

Beispiel 2 Der Median der Stichprobe $2,5,7,8$ ist $m=6$, da es $n=4$ (gerade) Werte gibt und die 6 der Durchschnitt der beiden Werte in der Mitte der geordneten Stichprobe ist.

Der Median ist, wie des arithmetische Mittel ein Lagemaß. Es beschreibt wo die Daten auf dem Zahlenstrahl liegen. Genauer gesagt, beschreibt der Median wo die Mitte der Daten auf dem Zahlenstrahl liegt.

Beachte: In den Berechnung des Medians gehen nicht genauen Werte der Stichprobe ein. Es ist allein der mittlere Wert der (oder die beiden mittleren Werte die) die $m$ bestimmt. Beispielsweise haben die beiden folgenden Stichproben den gleichen Median:

Stichprobe 1: $\quad 1,4,6,7,7,8,9$

Stichprobe 2: $\quad 3,4,6,7,9,30,74$

Der Median ist jeweils $7$. Aber das arithmetische Mittel ist für die erste Stichprobe $6$ und für die zweite Stichprobe $19$.

Eine andere Möglichkeit den Median zu beschreiben ist: Der Median ist ein Wert für den gilt

mindestens $50\%$ der Stichprobenwerte sind kleiner-gleich $m$ und
mindestens $50\%$ der Stichprobenwerte sind größer-gleich $m$ und

Quantile#

Quantile verallgemeinern die Idee des Medians folgendermaßen. Sei $x_1,\dots,x_n$ eine Stichprobe. Ein $0.3$-Quantil ist ein Wert $q$ für den gilt:

mindestens $0.3\cdot n$ der Stichprobenwerte sind kleiner-gleich $q$ und
mindestens $0.7\cdot n$ der Stichprobenwerte sind größer-gleich $q$ sind

Ist $0.3 \cdot n$ oder $0.7\cdot n$ keine ganze Zahl, so ist dieser Wert zunächst abzurunden. Die lässt sich mit der Gauß-Klammer $\lfloor x \rfloor$ schreiben: für $x\in \mathbb R$ ist

\[ \lfloor x \rfloor = max\{z\in\mathbb Z \mid z\leq x\}\]

als ist $\lfloor x \rfloor$ die größte ganze Zahl die kleiner-gleich $x$ ist. Damit können wir elegant definieren was ein Quantil ist:

Definition

Ein $\alpha$-Quantil $q_\alpha$ einer Stichprobe ist eine Zahl für die gilt, dass

mindestens $\lfloor\alpha\cdot n\rfloor$ der Stichprobenwerte sind kleiner-gleich $q_\alpha$ und
mindestens $\lfloor(1-\alpha)\cdot n\rfloor$ der Stichprobenwerte sind größer-gleich $q_\alpha$ sind

Quantile für metrisch messbare Daten#

Am häufigsten möchte man Quantile für metrisch messbare Daten bestimmen. Wie wir dabei vorgehen, wird hier besprochen. Zunächst geht es um die Eindeutigkeit der Quantile.

Ist $q_\alpha$ immer eindeutig?

Nein! Es gibt meist mehrere Werte, welche diese Eigenschaft erfüllen.

Beispiel

Sei $3,5,6,7,9,10,11,14$ eine Stichprobe und $\alpha=0.25$. Es sollen minestens $0.25\cdot 8=2$ der Werte kleiner gleich der gesuchten Zahl $q$ sein und $0.75\cdot 8=6$ der Werte sollen größer-gleich der gesuchten Zahl $q$ sein. Daher ist jedes $q$ mit

\[5\leq q\leq 6\]

ein $0.25$-Quantil der Stichprobe.

Wie wählen wir ein Quantil aus?

Dazu gibt es viele Ansätze, von denen viele auf unterschiedliche Werte führen. Allein in R gibt es in der vordefinierten Funktion quantile() neun verschieden Berechnungsmethoden, welche alle leicht unterschiedliche Werte liefern. In der Praxis und insbesondere für große Stichproben ist es meist vollkommen unerheblich welche Mehtode man wählt. Wir werden im Rahmen der Vorlesung immer die Standard-Methode von R nutzen. Diese liefert für obiges Beispiel den Werte $q_{0.25} = 5.75$

x<- c(3,5,6,7,9,10,11,14)
quantile(x,0.25)

25%: 5.75

Wie würde man das per Hand ausrechnen?

Sei $x_{(1)},x_{(2)},\dots,x_{(n)}$ die aufsteigend geordnete Stichprobe der Größe $n$ und $\alpha\in(0,1)$.

Berechne $n\cdot \alpha + (1-\alpha)$ und runde diese Zahl ab. Nenne das Ergebnis $j$.
Berechne $g = n\cdot \alpha + (1-\alpha) - j$.
Berechne $q_{\alpha} = (1-g)\cdot x_{(j)} + g \cdot x_{(j+1)} $

Beispiel

Sei $3,5,6,7,9,10,11,14$ wieder die Stichprobe und $\alpha=0.25$. Die drei Schritte lauten hier wie folgt:

$8 \cdot 0.25 + 0.75 = 2.75$ ergibt abgerundet $j=2$
$g=8 \cdot 0.25 + 0.75 - 2 =0.75$
$q_{0.25}= (1-0.75) \cdot x_{(2)} + 0.75 \cdot x_{(3)} = 0.25 \cdot 5 + 0.75 \cdot 6 = 5.75$

Eine R-Funktion, die diese Berechnungen durchführt ist:

qua <- function(x,p){
  n <- length(x)
  j <- floor(n*p+(1-p))
  g <- n*p+(1-p)- j
  xs <- sort(x)
  (1-g)*xs[j]+ g*xs[j+1]
}
# Beispiel
x<- c(3,5,6,7,9,10,11,14)
quantile(x,0.25)
qua(x,0.25)
# beide Funktionen liefern tatsächlich das gleiche

25%: 5.75

5.75

Beachte: Im Rahmen der Vorlesung wird es genügen die Quantile einer Stichprobe mit quantile()zu berechnen.

Wichtige Quantile

Häufig werden die Werte $q_{0.25}$, $q_{0.5}$ und $q_{0.75}$ berechnet.
Der Wert ist $q_{0.5}$ ist genau der Median.
Die Werte $q_{0.25}$ und $q_{0.75}$ heißen auch Quartile

Sonderfall: Ordinal messbare Daten#

Sind die Daten „nur“ ordinal messbar, so funktioniert obige Berechnungsmethode nicht. Dies liegt daran, dass man mit ordinalen Werten nicht rechnen kann, also ist insbesondere der Schritt 3 nicht ausführbar. Im Falle ordinal messbarer Daten ist es aber trotzdem möglich von Quantilen (und vom Median zu sprechen). Hier werden sie wie folgt gebildet.

Sei $x_{(1)},x_{(2)},\dots,x_{(n)}$ die aufsteigend geordnete Stichprobe der Größe $n$ zu einem ordinal messbaren Merkmal und $\alpha\in(0,1)$.

Berechne $\alpha \cdot n$.
Fallunterscheidung:
- Fall $\alpha \cdot n$ ist ganzzahlig: $q_\alpha = x_{(\alpha\cdot n)}$
- Fall $\alpha \cdot n$ ist nicht ganzzahlig: $q_\alpha = x_{(\lfloor\alpha\cdot n\rfloor +1)}$

Umsetzung in R: Nutze die Funktion quantile() mit der Option type=1, z.B. quantile(data, 0.25, type=1), siehe Quantile für ordinal messbare Daten

data <- factor(c("gering", "mittel", "hoch", "gering", "hoch", "mittel", "mittel", "hoch"),
               levels = c("gering", "mittel", "hoch"), ordered = TRUE)

sort(data)

quantile(data, 0.25, type=1)
quantile(data, 0.3, type=1)

gering
gering
mittel
mittel
mittel
hoch
hoch
hoch

Levels:

'gering'
'mittel'
'hoch'

25%: gering

Levels:

'gering'
'mittel'
'hoch'

30%: mittel

Levels:

'gering'
'mittel'
'hoch'

Interquartilsabstand#

Die 50% mittleren Werte der Stichprobe liegen zwischen den beiden Quartilen. Der Abstand dieser Quartile dient als ein Streuungsmaß und heißt Interquartilsabstand:

\[\text{IQR} = q_{0.75} - q_{0.25} \]

Geometrisches Mittel#

Für eine Stichprobe $x_1,\dots,x_n$, welche aus positiven reellen Zahlen besteht, ist das geometrische Mittel definiert als

\[ \bar x_{\text{geo}} = \sqrt[n]{x_1\cdot x_2 \cdot \ldots \cdot x_n} = \left(\prod_{i=1}^n x_i \right)^{\frac1n}\]

Eine typische Anwendung des geometrischen Mittels kommt aus der Zinsrechnung:

Beispiel

Ein Guthaben $G$ soll über 3 Jahre verzinst werden. Der Zinssatz im ersten Jahr beträgt $2\%$ im zweiten Jahr $3\%$ und im dritten Jahr $5\%$. Mit welchem konstanten Zinssatz hätte man $G$ über 3 Jahre verzinsens können um auf den gleiche Betrag zu kommen?

Rechnung: Nach 3 Jahre beträgt das Gesamtguthaben $H$:

\[H:= G \cdot 1.02 \cdot 1.03 \cdot 1.05\]

Wir suchen die Zahl $q$ für die gilt

\[ G \cdot 1.02 \cdot 1.03 \cdot 1.05 = G \cdot q^3\]

Stellen wir dies nach $q$ um erhalten wir

\[q= \sqrt[3]{1.02\cdot 1.03\cdot 1.05} = 1.033258\]

Antwort: Eine 3 jährige Verzinsung mit $3.3258\%$ führt zum gleichen Guthaben wie die obige Verzinsung.

Zusammenfassung und Bemerkungen#

Die hier eingeführten Kennzahlen werden oft mit den Zusatz „Stichproben-“ oder „empirische(r)“ bezeichnet, z.B. Stichprobenvarianz oder empirische Standardabweichung. Ein solcher Zusatz ist wichtig, da diese Begriff auch im Kontext von Zufallvariablen verwendet werden und dort eine (leicht) andere Bedeutung haben.
Je nach Art der Messbarkeit des zu untersuchenden Merkmals sind nicht alle der Kennzahlen verwendbar:
- Stichproben-Mittelwert, -Varianz, -Standardabweichung, Variationskoeffizient nur sinnvoll für metrisch skalierte Merkmale.
- Quantile, Median und Quartilsabstand sind sind sinnvoll für metische skalierte Merkmale, aber auch (mit leichten Anpassungen in der Definition) für ordinal skalierte Merkmale
- Für nominal skalierte Merkmale ist von den hier aufgeführten Maßzahlen nur der Modalwert sinnvoll zu bestimmen.
Quantile, Median und Quartilsabstand sind nicht eindeutig. Nutzen Sie daher im Rahmen der Vorlesung und Prüfung für metrisch skalierte Merkmale die spezielle Definition von $q_\alpha$. Diese ist gleich der Standand Berechnungsmethode in R.

Bemerkung: Sinnvolle Auswertungen nach Skalenniveau

Nominalskala
- Häufigkeiten durch Zählen der einzelnen Ausprägungen
- geeignetes Lagemaß: Modalwert
- kein sinnvolles Streuungsmaß
Ordinalskala
- Häufigkeiten durch Zählen der einzelnen Ausprägungen
- geeignetes Lagemaß: Modalwert, Median
- geeignetes Streuungsmaß: Interquartilsabstand, Spannweite (je mit Angabe von … bis … da keine Differenzen gebildet werden dürfen)
metrische Skala
- Häufigkeiten durch Zählen der einzelnen Ausprägungen
- geeignetes Lagemaß: Modalwert, Median, arithmetisches Mittel, geometrisches Mittel, …
- geeignetes Streuungsmaß: Interquartilsabstand, Spannweite, Standardabweichung, Varianz,…

Vereinfachte Berechnung#

Die Berechnung der Maßzahlen per Hand, etwa über Eingabe in einen Taschenrechner, kann sehr mühsam und fehleranfällig sein. Nach Möglichkeit sollte man dies vermeiden und stattdessen eine geeignete Software (z.B. R) nutzen.

Sollte ein Eigabe per Hand aber nötig sein, so kann folgende Vereinfachung der Formeln helfen: Sind die Stichproben mit ihren Häufigkeiten gegeben, so enthalten viele der Formeln gleiche Summanden, welche wir zusammenfassen können. Hat die Stichprobe $x_1,\dots,x_n$ die Ausprägungen $a_1,\dots,a_k$ mit den absoluten Häufigkeiten $h_1,\dots,h_k$, so gilt

\[\begin{split}\begin{align*}\bar x&= \frac1n \sum_{i=1}^n x_i = \frac1n \sum_{j=1}^k h_j\cdot a_j \\ s^2 &= \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2 = \frac{1}{n-1} \sum_{j=1}^{k} h_j\cdot (a_j - \bar{x})^2 \end{align*}\end{split}\]