Stetige Gleichverteilung

Die stetige Gleichverteilung beschreibt einen Zufälligen Vorgang, bei dem

• alle Werte aus einem fest vorgegebenem Intervall auftreten können und

• kein Bereich in dem Intervall gegenüber anderen Bereichen bevorteilt ist, also mit höherer Wahrscheinlichkeit getroffen wird

Dies beschreibt man mit einer, im vorgegebenen Intervall, konstanten Wahrscheinlichkeitsdichte:

Definition

Seien \(a\) und \(b\) reelle Zahlen mit \(a<b\). Dann heißt \(X\) auf dem Intervall \(I=[a,b]\) stetig gleichverteilt auf \(I\), falls \(X\) die Wahrscheinlichkeitsdichte

\[\begin{split}f:\mathbb R\to\mathbb R,\qquad f(x)=\begin{cases}\frac{1}{b-a}& \text{falls }x\in I \\0 & \text{sonst.}\end{cases}\end{split}\]

hat. Wir schreiben dann

\[f\sim U(I)\]

Die Verteilungsfunktion ist in diesem Fall

\[\begin{split}F:\mathbb R \to [0,1],\qquad F(x)=\begin{cases} 0 & \text{falls }x<a\\ \frac{x-a}{b-a}&\text{falls }a\leq x\leq b \\1 & \text{sonst.}\end{cases}\end{split}\]

In obiger Definition lässt sich \(I\) auch durch eins der folgenden Intervalle ersetzen:

\[(a,b),\quad (a,b],\quad [a,b)\]

Anwendungen

Hier sind ein paar kurze Anwendungsbeispiele für die stetige Gleichverteilung:

• Zufällige Wartezeit an einer Bushaltestelle
  Ein Bus fährt alle 10 Minuten. Wenn eine Person zufällig zur Haltestelle kommt, ist die Wartezeit gleichmäßig zwischen 0 und 10 Minuten verteilt.

• Zufällige Startzeit eines Events innerhalb einer Stunde
  Eine Veranstaltung kann irgendwann zwischen 14:00 und 15:00 Uhr beginnen, wobei jede Startzeit innerhalb dieser Stunde gleich wahrscheinlich ist.

• Fehlerhafte Messgeräte
  Ein ungenaues Messgerät zeigt Werte mit einem zufälligen Fehler, der gleichmäßig zwischen ±0,5 Einheiten verteilt ist.

• Punkt auf einer Strecke
  Ein Punkt wird zufällig auf einer 1 Meter langen Strecke platziert, wobei jede Position gleich wahrscheinlich ist.

Eigenschaften

Sei \(X\sim U([a,b])\). Dann gilt

\[\mathbb E(X)=\frac{a+b}{2}\]

und

\[\mathrm{Var}(X)=\frac{(b-a)^2}{12}\]

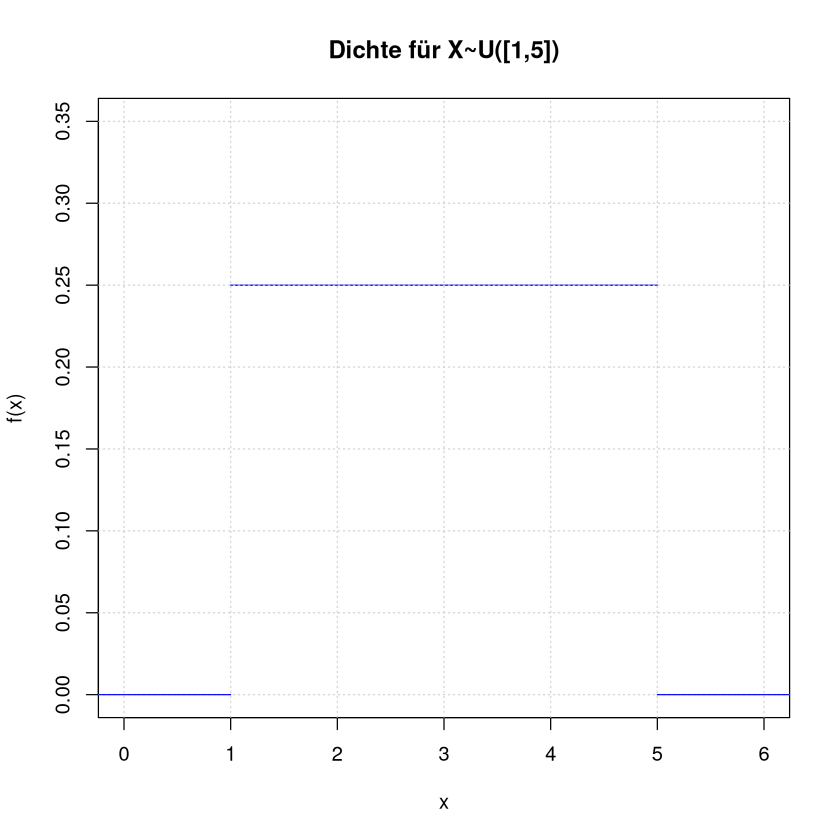
Verlauf der Dichte

plot(c(1,5),c(0.25,0.25),type = "l",
     col="blue",xlim=c(0,6),ylim=c(0,0.35),
     main="Dichte für X~U([1,5])",
     xlab="x",ylab="f(x)"
    )
grid()
points(c(-1,1),c(0,0),type="l",col="blue")
points(c(5,7),c(0,0),type="l",col="blue")

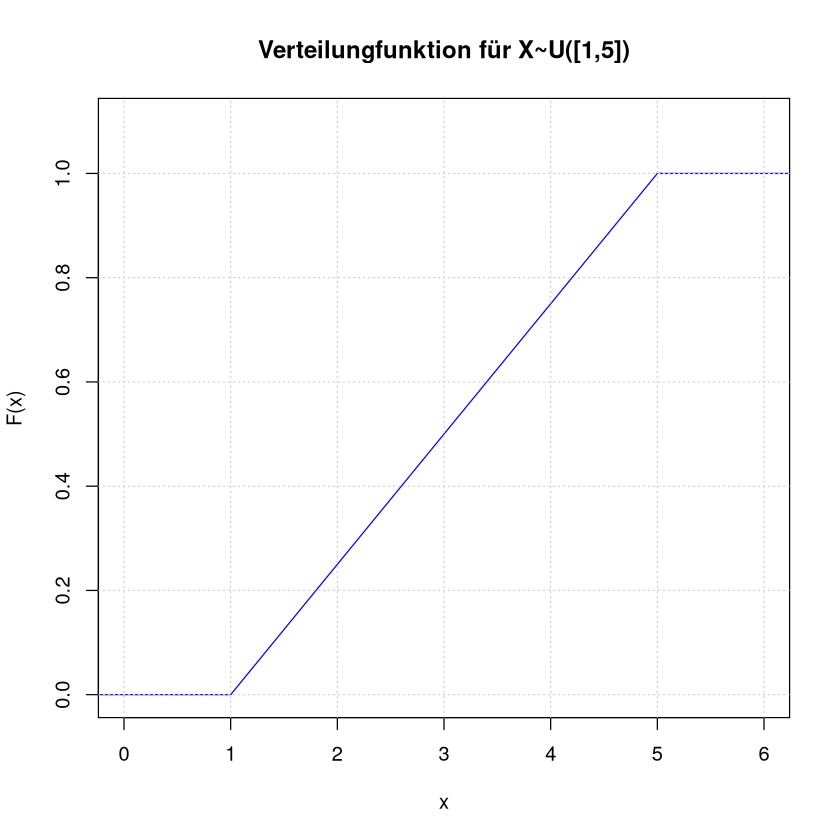
Verlauf der Verteilungsfunktion

plot(c(-1,1,5,7),c(0,0,1,1),type = "l",
     col="blue",xlim=c(0,6),ylim=c(0,1.1),
     main="Verteilungfunktion für X~U([1,5])",
     xlab="x",ylab="F(x)"
    )
grid()

Beispiel

Beispiel: Wartezeit an der Bushaltestelle

Ein Bus fährt alle 10 Minuten nach einem festen Fahrplan. Eine Person kommt zufällig zur Haltestelle, ohne den Fahrplan zu kennen. Ihre Wartezeit (in Minuten) bis zum nächsten Bus ist gleichmäßig zwischen 0 und 10 Minuten verteilt.

1. Wie hoch ist die Wahrscheinlichkeit, dass die Wartezeit höchstens 4 Minuten beträgt?

2. Wie hoch ist die Wahrscheinlichkeit, dass die Wartezeit zwischen 3 und 8 Minuten liegt?

3. Für welche Wartezeit \(t\) gilt „Die Wahrscheinlichkeit, dass man maximal \(t\) Minunten wartet ist gleich \(0.9\)“?

4. Wie groß ist der Erwartungswert der Wartezeit?

---

Lösung

1. Definition der Zufallsvariable

   \(X\) … Wartezeit in Minuten. Die Zufallsvariable \(X\) ist gleichmäßig auf dem Intervall ([0,10]) verteilt, kurz \(X\sim U([0,10])\)

2. Angeben von Dichte und Verteilungfunktion

   • Dichtefunktion \(f:\mathbb R\to\mathbb R\):

     \[\begin{split} f(x) = \begin{cases}0.1 & \text{falls } x \in [0,10]\\ 0 & \text{sonst.}\end{cases}\end{split}\]

   • Verteilungsfunktion \(F:\mathbb R\to\mathbb R\):

     \[\begin{split} F(x) = \begin{cases} 0 &\text{falls } x < 0 \\ \frac{x}{10} &\text{falls } 0 \leq x \leq 10 \\ 1 &\text{falls } x > 10 \end{cases}\end{split}\]

3. Berechnung der konkreten Antworten:

   • Aufgabe 1: Gesucht ist \(\mathbb P(X \leq 4)\)

     \[\mathbb P(X \leq 4) = F(4) = \frac{4}{10} = 0.4\]

     Antwort: Die Wahrscheinlichkeit, dass die Wartezeit höchstens 4 Minuten beträgt, ist 0.4 (40%).

   • Aufgabe 2: Gesucht ist \(\mathbb P(3 \leq X \leq 8)\)

     \[\mathbb P(3 \leq X \leq 8) = F(8) - F(3) = \frac{8}{10} - \frac{3}{10} = 0.5\]

     Antwort: Die Wahrscheinlichkeit, dass die Wartezeit zwischen 3 und 8 Minuten liegt, ist 0.5 (50%).

   • Aufgabe 3: Gesucht ist \(t\) mit \(\mathbb P(X \leq t)=0.9\)

     Wegen \(F(t)=\mathbb P(X \leq t)=0.9\) ist gerade das 0.9-Quantil gesucht. Wir stellen also die Verteilungsfunktion nach \(t\) um:

     \[\begin{split} \begin{align*} F(t)=0.9 \quad &\Leftrightarrow \quad \frac{t-0}{10-0} = 0.9 \\ &\Leftrightarrow \quad t = 0.9 \cdot 10 = 9 \end{align*} \end{split}\]

   • Aufgabe 4: Gesucht ist \(\mathbb E(X)\)

     \[E(X)=\frac{a+b}2 = 5\]

     Antwort: Der Erwartungswert der Wartezeit beträgt 5 Minuten.

Beachte: Man hätte die Wahrscheinlichkeiten natürlich auch mit einem Intergral über die Dichte oder mit einfachen geometrischen Berechnungen (Rechteck) mit der Dichte durchführen können.

Umsetzung mit R

# Sei X gleichverteilt auf [0,10]

# Wert der Dichte an x=3
dunif(3, min = 0, max = 10)

# Wert der Verteilungsfunktion an x=3
punif(3, min = 0, max = 10)

# 20 auf Realisierungen der Zufallsvariable X
set.seed(987)
runif(20, min = 0, max = 10)

0.1

0.3

1. 4.77267141221091
2. 9.90614708745852
3. 6.06417875271291
4. 5.76612946111709
5. 8.09069278417155
6. 2.32308145845309
7. 4.24518776824698
8. 3.4897033800371
9. 8.6448589595966
10. 7.10149414371699
11. 1.85725438874215
12. 3.81133480696008
13. 1.69796965550631
14. 3.11530970735475
15. 1.9603824801743
16. 6.38918904354796
17. 1.32849905407056
18. 9.66582182794809
19. 0.987465926446021
20. 7.09454959491268

# Nun ein Plot aus 300 Punkten
# die x und y Koordinate soll jeweils (unabhängig)
# auf [0,10] gleichverteilt sein
set.seed(567)
x <- runif(300, min = 0, max = 10)
y <- runif(300, min = 0, max = 10)
plot(x,y)