Normalverteilung#
Die Normalverteilung ist eine der am häufigsten genutzten Wahrscheinlichkeitsverteilungen. Sie hat zahlreiche Anwendungsgebiete in Theorie und Praxis.
Definition#
Definition
Eine Zufallsvariable \(X\) heißt normalverteilt mit den Parametern \(\mu\) und \(\sigma^2\), (\(\mu\in\mathbb R\), \(\sigma>0\)), wenn sie die Dichte
besitzt. Wir schreiben dann
Gilt \(\mu=0\) und \(\sigma^2=1\), so sprechen wir von der Standardnormalverteilung.
Da es für \(f\) keine Stammfunktion gibt, lässt sich die Verteilungsfunktion nicht in geschlossener Form angeben. Mögliche Darstellungsformen sind
Darstellung als Integral
Darstellung als Reihe (unendliche Summe)
Dies führt dazu, dass Wahrscheinlichkeiten (früher) oft mit Hilfe von Wertetabellen der Verteilungsfunktion berechnet wurden. Wir nutzen hierfür natürlich R, siehe Umsetzung in R.
Anwendungen#
Szenarien, in denen die Normalverteilung genutzt wird bzw. genutzt werden kann:
Körpergröße in einer Bevölkerung
Die Verteilung der Körpergrößen bei Erwachsenen folgt näherungsweise einer Normalverteilung.Messfehler in Experimenten
Kleine zufällige Fehler bei Messungen (z. B. Temperaturmessung) sind oft normalverteilt.IQ-Werte
Intelligenzquotienten in der Bevölkerung sind standardisiert und folgen etwa einer Normalverteilung mit Mittelwert 100 und Standardabweichung 15.Punkteverteilungen bei großen Prüfungen
Bei sehr vielen Teilnehmenden streben Punkteverteilungen manchmal eine Normalverteilung an.Produktionsprozesse (Qualitätskontrolle)
Abweichungen z. B. in der Länge von Schrauben bei maschineller Herstellung können normalverteilt sein.Finanzmodelle (z. B. Renditen)
In vereinfachten Finanzmodellen werden tägliche Kursänderungen von Aktien oft als normalverteilt angenommen.Blutdruckwerte in der Medizin
Bei gesunden Erwachsenen sind Blutdruckwerte näherungsweise normalverteilt.Verbrauch von Haushaltsstrom
Der tägliche Stromverbrauch pro Haushalt kann bei vielen Haushalten einer Normalverteilung ähneln.Reaktionszeiten bei Experimenten
In der Psychologie werden Reaktionszeiten häufig als normalverteilt modelliert.Weitwurf und Weitsprung
Die Wurf- oder Sprungweiten einer Sportlerin variieren leicht von Versuch zu Versuch und können normalverteilt sein.
Eigenschaften#
Gitl \(X\sim \mathrm{N}(\mu,\sigma^2)\), so
Die beiden Parameter entsprechen also den wichtigsten Kenngrößen der Verteilung.
Weiterhin gilt für die Normalverteilung
Die Dichte der Normalverteilung mit Erwartungswert \(\mu\) ist spiegelsymmetrisch zur Geraden \(x=\mu\).
Der Erwartungswert ist immer gleich dem Median.
Ist \(X\sim\mathrm N(\mu,\sigma^2)\), so gilt
\(\mathbb P(\mu-\sigma \leq X \leq \mu + \sigma )\approx 0.683\)
\(\mathbb P(\mu-2\sigma \leq X \leq \mu + 2\sigma )\approx 0.954\)
\(\mathbb P(\mu-3\sigma \leq X \leq \mu + 3\sigma )\approx 0.997\)
Jede normalverteilte Zufallsvariable \(X\sim\mathrm N(\mu,\sigma^2)\) lässt sich durch
\[ Y = \frac{X-\mu}{\sigma}\]in eine standardnormalverteilte Zufallsvariable transformieren, d.h. für dieses \(Y\) gilt \(Y\sim \mathrm N(0,1)\).
Dieser Fakt führt dazu, dass man jede beliebige Normalverteilung auf die Standardnormalverteilung zurückführen kann und entsprechende Wahrscheinlichkeiten mit der Verteilungsfunktion der Standardnormalverteilung \(\Phi\) berechnen kann.
Die Verteilungsfunktion der Standardnormalverteilung ist punktsymmetrisch zum Punkt \((0,0.5)\). Es gilt
\[\Phi(-x)=1-\Phi(x)\]
Rechenregeln
Ist \(X\sim \mathrm N(\mu,\sigma^2)\) und \(\Phi\) die Verteilungsfunktion der Standardnormalverteilung, dann gilt
\(\mathbb P(X\leq t) = \Phi\left(\frac{t-\mu}{\sigma}\right)\)
\(\mathbb P(X\geq t) = 1-\Phi\left(\frac{t-\mu}{\sigma}\right)\)
\(\mathbb P(s\leq X\leq t) = \Phi\left(\frac{t-\mu}{\sigma}\right) - \Phi\left(\frac{s-\mu}{\sigma}\right)\)
Die Summe aus zwei unabhängigen normalverteilten Zufallsvariablen ist wieder normalverteilt, wobei
der Erwartungswert der Summe gleich der Summe der Erwartungswerte ist
die Varianz der Summe gleich der Summe der Varianzen ist.
Kurz: Sind \(X\sim\mathrm N(\mu_1,\sigma_1^2)\) und \(Y\sim\mathrm N(\mu_2,\sigma_2^2)\) unabhängig, so gilt
\[ X+Y \sim \mathrm N(\mu_1+\mu_2, \sigma_1^2+ \sigma_2^2)\]Achtung: Die Standardabweichung von \(X+Y\) ist dann \(\sqrt{\sigma_1^2 +\sigma_2^2}\).
Gilt \(X\sim \mathrm N(\mu,\sigma^2)\) so ist \(Y=aX+b\) für beliebige \(a,b\in \mathbb R\) ebenfalls normalverteilt mit
\[ Y\sim N(a\mu+b , (a\sigma)^2 )\]
Die Kombination von 2. und 3. ergibt z.B.: Sind \(X\sim\mathrm N(\mu_1,\sigma_1^2)\) und \(Y\sim\mathrm N(\mu_2,\sigma_2^2)\) unabhängig, so gilt
\[ X-Y \sim \mathrm N(\mu_1-\mu_2, \sigma_1^2+ \sigma_2^2)\]Für jedes \(\alpha\in (0,1)\) lässt sich eindeutig das \(\alpha\)-Quantil \(\Phi^{-1}(\alpha)\) der Standardnormalverteilung angeben. Es wird typischweise mit \(z_\alpha\) bezeichnet. Dies ist also die Zahl für die gilt:
\[\Phi(z_\alpha)=\alpha\]Wir berechnen diese Werte mit R, siehe Umsetzung in R.
Beispiel#
Beispiel
Auf der antarktischen Pinguin-Olympiade wird der Fischweitwurf treten Pinguine im Fischweitwurf an. Die geworfene Distanz (in Metern) sei normalverteilt mit Mittelwert \(\mu = 10\ \text{m}\) und Standardabweichung \(\sigma = 1.5\ \text{m}\).
Hintergrund: Pinguine werfen tote Fische, um ihre Fitness zu zeigen - sie versuchen damit die Pinguininnen zu beeindrucken und zur Paarung zu überzeugen. 🎣 🐧
Modellierung:
\(X\) … Zufallsvariable, welche die Wurfweite eines zufällig ausgewählten Pinguins und Wurfs in m angibt.
Es gilt laut Aufgabentext: \(X\sim \mathrm N(10,1.5^2)\)
Frage:
„Wie hoch ist die Chance, dass Pinguin Frido beim nächsten Wurf seinen Rekord bricht und den Fisch weiter als 13 Meter wirft?“ 🥇Lösung:
\[\mathbb P(X>13)=1-\Phi\left(\frac{13-10}{1.5}\right) = 1-\Phi(2) = 1 - 0.9772= 0.0228\]Antwort: Die Wahrscheinlichkeit beträgt nur 2,28% - das sieht nicht gut aus für Frido. 👎
Hinweis: Den Zahlenwert von \(\Phi(2)\) berechnet man in R mit
pnorm(2)oder man entnimmt ihn altmodisch einer Tabelle.
Frage:
„Wegen regelmäßiger Unfälle will die Jury nun eine Sicherheitszone markieren, in der 99% aller Fische landen. Wie weit muss der Absperrzaun vom Abwurfort entfernt sein, damit kein Zuschauer-Pinguin getroffen wird?“Lösung:
Gesucht ist \(t\in \mathbb R\) mit der Eigenschaft \(\mathbb P(X\leq t)=0.99\). Wir stellen diese Gleichung nach \(t\) um:
\[\begin{split} \begin{align*} 0.99= \mathbb P(X\leq t) \quad & \Leftrightarrow \quad 0.99= \Phi\left(\frac{t-10}{1.5}\right) \\ \quad & \Leftrightarrow \quad \Phi^{-1}(0.99)= \frac{t-10}{1.5} \\ \quad & \Leftrightarrow \quad z_{0.99}= \frac{t-10}{1.5} \\ \quad & \Leftrightarrow \quad t = z_{0.99}\cdot 1.5 + 10 \approx 13.49\\ \end{align*} \end{split}\]Antwort: 99% der Fische werden nicht weiter als 13,49 m geworfen. In diesem Abstand ist man sicher. Falls doch jemand weiter wirft ist sicherlich Doping im Spiel! 💉 💪
Hinweis: Den Zahlenwert \(z_{0.99}= 2.326348\) berechnet man in R mit
qnorm(0.99)oder entnimmt ihn altmodisch einer Tabelle.
Frage:
„Pinguin Arnold hat das ganze Jahr trainiert. Für ihn gelten andere Wahrscheinlichkeiten: Er wirft im Mittel 11 m. Nach vielen Versuchen stellt sich heraus, dass 80% seiner Würfe zwischen 9 und 13 Metern landen. Bestimmen Sie die Standardabweichung \(\sigma_A\) für Arnold.“ 🦾Lösung:
Neue Zufallsvariable \(Y\sim \mathrm N(11,\sigma_A^2)\). Wir suchen \(\sigma_A\) mit \(\mathbb P(9\leq X \leq 13)=0.80\)
\[\begin{split} \begin{align*} \mathbb P(9\leq Y \leq 13)=0.8 \quad & \Leftrightarrow \quad 0.8= \Phi\left(\frac{13-11}{\sigma_A}\right)-\Phi\left(\frac{9-11}{\sigma_A}\right) \\ & \Leftrightarrow \quad 0.8= \Phi\left(\frac{2}{\sigma_A}\right)-\Phi\left(-\frac{2}{\sigma_A}\right) \\ & \Leftrightarrow \quad 0.8= \Phi\left(\frac{2}{\sigma_A}\right)-\left(1-\Phi\left(\frac{2}{\sigma_A}\right)\right) \\ & \Leftrightarrow \quad 0.8= 2\Phi\left(\frac{2}{\sigma_A}\right)-1\\ & \Leftrightarrow \quad \frac{0.8+1}{2}= \Phi\left(\frac{2}{\sigma_A}\right)\\ & \Leftrightarrow \quad z_{0.9}= \frac{2}{\sigma_A}\\ & \Leftrightarrow \quad \sigma = \frac{2}{z_{0.9}}=\frac{2}{1.281552} \approx 1.56 \\ \end{align*} \end{split}\]Antwort: Die Standardabweichung für Arnold ist mit etwa 1,56 m größer als bei den anderen. Er wirft zwar im Mittel besser, aber nicht ganz so zuverlässig wie die anderen.
Frage: „Im Finale trifft Frido auf Arnold. Jeder hat genau einen Wurf. Wie groß ist die Wahrscheinlichkeit, dass Frido gewinnt?“ 🥇
Gesucht ist die Wahrscheinlichkeit \(\mathbb P(X\geq Y)\). Dies schreiben wir folgendermaßen um:
\[\mathbb P(X\geq Y)=\mathbb P(X-Y\geq 0)\]Wir nehmen an, dass Wurfweiten der Pinguine stochastisch unabhängig sind und wissen daher, dass \(X-Y\) wieder normalverteilt ist mit
\[ X-Y \sim \mathrm N(10 - 11, 1.5^2 + 1.56^2)\]also gilt
\[ \begin{align*} \mathbb P(X-Y \geq 0)=1-\Phi\left(\frac{0- (-1)}{\sqrt{1.5^2 + 1.56^2}}\right)=1-\Phi(0.46207)= 0.3220 \end{align*} \]Antwort: Trotz dass Frido das ganz Jahr über nicht trainiert hat, gewinnt er noch mit einer Wahrscheinlichkeit von 32.2%. Viel Glück Frido. 🍀
Umsetzung in R#
Die wichtigsten Funktionen sind
dnorm()… für die Wahrscheinlichkeitsdichte der Normalverteilungpnorm()… für die Verteilungsfunktion der Normalverteilungqnorm()… zum Berechnen der Quantile der Normalverteilungrnorm()… zum Erzeugen von Pseudozufallszahlen aus der Normalverteilung
Es ist dabei jeweils möglich mit den Argumenten mean= und sd= den Mittelwert und die Standardabweichung zu spezifizieren. Wird nichts angegeben, so verwenden die Funktionen die Werte für die Standardnormalverteilung mean=0 und sd=1.
Achtung: In der R-Funktionen gibt man die Standardabweichung an, wir schreiben in \(\mathrm N(\mu,\sigma^2)\) die Varianz.
# Pinguinaufgaben in R
# Aufgabe 1
cat("Aufgabe 1:\n")
pnorm(13,mean=10,sd=1.5,lower.tail = F)
1-pnorm(13,mean=10,sd=1.5)
1-pnorm((13-10)/1.5)
# Aufgabe 2
cat("\nAufgabe 2:\n")
qnorm(0.99,mean=10,sd=1.5)
qnorm(0.99)*1.5 + 10
# Aufgabe 3
cat("\nAufgabe 3:\n")
2/qnorm(0.9)
# Aufgabe 4
cat("\nAufgabe 4:\n")
1-pnorm(0,-1,sqrt(1.5^2+1.56^2))
Aufgabe 1:
Aufgabe 2:
Aufgabe 3:
Aufgabe 4:
# Pseudozufallszahlen
# Setze den Zufallszahlengenerator
set.seed(123)
# Erzeuge normalverteilte Zufallszahlen
x <- rnorm(1000, mean = 0, sd = 1)
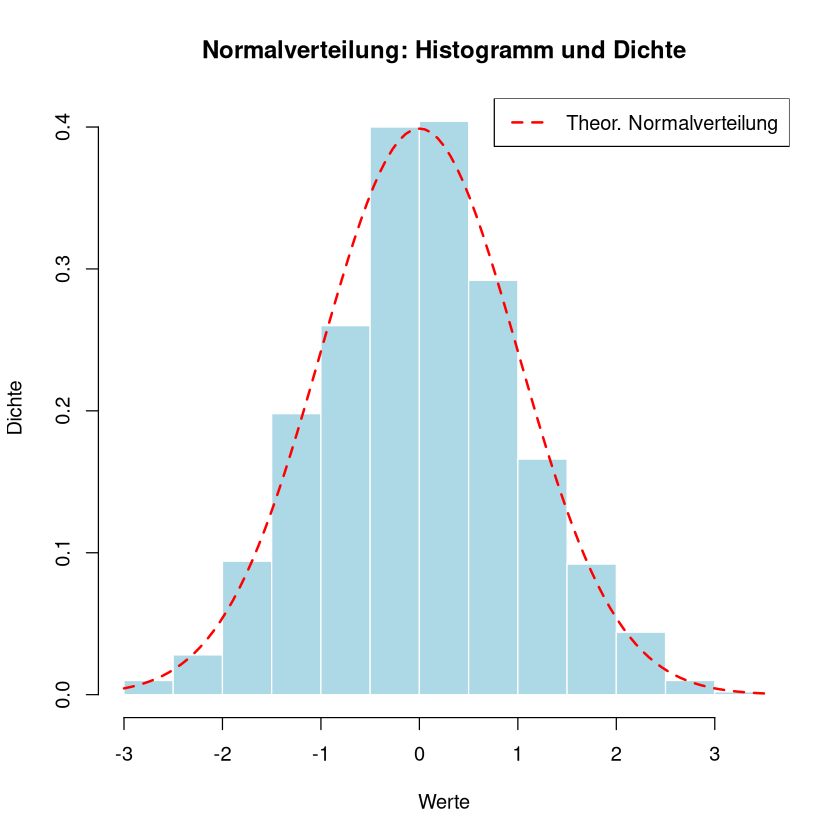
# Erstelle Histogramm mit Dichte-Skalierung
hist(x, probability = TRUE,
col = "lightblue", border = "white",
main = "Normalverteilung: Histogramm und Dichte",
xlab = "Werte", ylab = "Dichte")
# Füge theoretische Normalverteilung hinzu
curve(dnorm(x, mean = 0, sd = 1),
col = "red", lwd = 2, lty = 2, add = TRUE)
# Legende
legend("topright", legend = c("Theor. Normalverteilung"),
col = c("red"), lwd = 2, lty = c(2))
Normalverteilung - Warum bist du so normal?#
Die Normalverteilung taucht in der Realität und Natur in extrem vielen Situationen auf.
Ein besonderer Grund dafür ist der zentrale Grenzwertsatz. Wird ein Zufallsexperiment oft wiederholt und diese Ergebnisse aufaddiert, so verhalten sich diese Größen nahzu wie normalverteilte Zufallsvariablen. Das ist besonders erstaunlich, da es dabei nicht auf die ursprüngliche Verteilung im Zufallsexperiment ankommt. Exakt ausformuliert lautet dieser Satz wie folgt:
Zentraler Grenzwertsatz
Seien \(X_1,X_2,\dots \) eine Folge von Zufallsvariablen, welche
stochastisch unabhängig und
alle identisch verteilt sind (also alle die gleiche Verteilungsfunktion haben).
Ist \(S_n = X_1+ \dots + X_n\) die Summe der ersten \(n\) Zufallsvariablen und ist \(Y_n\) die normierte Version von \(S_n\), d.h.
so stimmt die Verteilungsfunktion von \(Y_n\) für wachsendes \(n\) immer mehr mit \(\Phi\) (der Verteilunsfunktion der Standardnormalverteilung) überein:
Bemerkung
Im Satz ist implizit vorausgesetzt, dass \(\mathbb E(X_1)=:\mu\) und \(\mathrm{Var}(X_1)=:\sigma^2\) existieren.
Mit den obigen Bezeichnungen gilt:
\(\mathbb E(S_n)=n\mu\) und \(\mathrm{Var}(S_n)= n\sigma^2\)
\(Y_n = \frac{S_n - n\mu}{\sqrt{n}\sigma}\)
Die Größen \(S_n\) und \(Y_n\) sind mit den entsprechenden Erwartungswerten und Varianzen nahezu normalverteilt. Dies schreiben wir als
\[S_n \stackrel{a}{\sim}\mathrm N(n\mu, n\sigma^2),\quad \text{und}\quad Y_n \stackrel{a}{\sim}\mathrm N(0, 1)\]Dies bedeutet, dass man für großes \(n\) statt mit der richtigen Verteilung auch mit der Normalverteilung rechnen kann (ohne einen zu großen Fehler zu machen).
Außerdem folgt sofort aus dem Satz: Unter den Voraussetzungen des Satzes ist auch der Mittelwert \(\bar X=\frac1n (X_1+\dots+X_n)\) mit entsprechendem Erwartungwert und entsprechender Varianz nahezu normalverteilt:
\[\bar X \stackrel{a}{\sim}\mathrm N(\mu, \frac{\sigma^2}{n})\]
Interpretation
Der Zentrale Grenzwertsatz besagt, dass die Summe (oder der Durchschnitt) vieler unabhängiger Zufallsvariablen - selbst wenn diese selbst nicht normalverteilt sind - unter bestimmten Bedingungen approximativ normalverteilt ist, sobald die Anzahl der Variablen groß genug ist.
Das bedeutet: Viele Prozesse in der Natur und im Alltag entstehen durch das Zusammenwirken vieler kleiner, zufälliger Einflüsse. Genau deshalb sieht man in der Praxis so oft eine Normalverteilung - sie ist das Ergebnis vieler kleiner Zufälligkeiten, die sich überlagern.
Beispielsweise:
Körpergröße von Menschen: Sie wird von vielen genetischen und Umweltfaktoren beeinflusst. Jeder einzelne Faktor wirkt nur ein bisschen, aber zusammen führen sie zu einer annähernd normalverteilten Körpergröße in der Bevölkerung.
Messfehler bei Experimenten: Wenn man einen physikalischen Wert mehrfach misst, wirken viele kleine Störfaktoren (z. B. Temperaturschwankungen, Messgeräteungenauigkeit). Die Verteilung der Messfehler nähert sich dadurch meist einer Normalverteilung an.
Beispiel
Bei der legendären Schneckenpost-Staffel treten 50 hochmotivierte Schnecken pro Team an. Jede Schnecke kriecht 1 Meter weit, übergibt dann den Staffelstab (und eine Mini-Postkarte) an die nächste Schnecke des Teams. Erst wenn eine Schnecke fertig ist, darf die nächste loskriechen. 🐌➡️🐌➡️🐌
Die Zeit, die eine einzelne Schnecke für ihren Meter braucht, ist zufällig, mit einem Erwartungswert von 3 Minuten und einer Standardabweichung von 0,5 Minuten, aber identisch verteilt. Die Kriechzeiten sind nicht normalverteilt, da manche Schnecken auf halber Strecke einschlafen oder spontane Stretchingpausen einlegen.
Wie groß ist die Wahrscheinlichkeit, dass die Gesamtzeit von Team 1 (also die Summe der 50 Einzelzeiten) unter 145 Minuten bleibt?
Der Trainer möchte auf Nummer sicher gehen: Mit welcher Zeitgrenze \(t\) muss er rechnen, wenn das Team 1 mit 90% Wahrscheinlichkeit spätestens dann beendet sein soll?
Nutze den zentralen Grenzwertsatz!
Lösung:
Variablen:
\(X_i\) … Zeit von Schnecke \(i\) aus dem Team, \(i=1,\dots,50\)
\(S_{n} = X_1+\dots+ X_{n}\) … Gesamtzeit eines Teams mit \(n\) Schnecken
Es gilt \(\mathbb E(X_i)=3\) und \(\mathrm{Var}(X_i)=0.5^2=0.25\) und daher
Wegen des zentralen Grenzwertsatzes gilt für großes \(n\):
zu Aufgabe 1:
Gesucht ist \(\mathbb P(S_{50}\leq 145)\)
\[\mathbb P(S_{50}\leq 145) \approx \Phi\left(\frac{145 - 3\cdot 50}{\sqrt{0.25\cdot 50}}\right)= \Phi(-1.4142)= 0.0787\]zu Aufgabe 2:
Gesucht ist \(t\) mit \(\mathbb P(S_{50}\leq t)=0.9\). Dies approximieren wir mit dem zentralen Grenzwertsatz und stellen daher \( \Phi(\frac{t-150}{\sqrt{0.25\cdot 50}})=0.9\) nach \(t\) um:
\[\begin{split} \begin{align*} \Phi(\frac{t-150}{\sqrt{0.25\cdot 50}})=0.9 \quad &\Leftrightarrow \quad \frac{t-150}{\sqrt{0.25\cdot 50}} = \Phi^{-1}(0.9) \\ &\Leftrightarrow \quad t = \Phi^{-1}(0.9) \cdot \sqrt{0.25\cdot 50}+150 = 154.53 \\ \end{align*} \end{split}\]
Tweetback#
Hier haben Sie in der Vorlesung die Möglichkeit Ihr Wissen zu prüfen.