Grundlagen#
Was ist eine Zufallsvariable?#
Zunächst ist zu klären, was eine Zufallsvariable überhaupt ist. Wir fangen mit ein paar Beispielen an, in denen \(X\) jeweils ein Zufallsvarible ist:
Dreimaliger Münzwurf: Wir werfen dreimal hintereinander eine Münze (mit jeweils den möglichen Ergebnissen K und Z). Dann können die folgenden Ergebisse auftreten:
\[\Omega=\{\text{KKK}, \text{KKZ}, \text{KZK}, \text{KZZ}, \text{ZKK}, \text{ZKZ}, \text{ZZK}, \text{ZZZ}\}\]Wir sagen nun die Variable \(X\) ist die Anzahl von \(\text K\) beim dreimaligen Münzwurf. Dann kann \(X\) die Werte
\[\{0,1,2,3\}\]annehmen. Welchen konkreten Wert \(X\) annimmt, hängt vom Ausgang des Zufallsexperiments ab.
Zwei Würfel: Wir werfen zwei Würfel. Dann können wir den Ergebnisraum diese Zufallsexperimts mit \(\{(1,1), (1,2), \dots , (6,6)\}\) beschreiben, siehe dieses Beispiel. Die Variable \(X\) sei nun die Summe der geworfenen Zahlen. Dann kann \(X\) die Werte
\[\{2,3,4,5,6,7,8,9,10,11,12\}\]annehmen. Welchen konkreten Wert \(X\) annimmt, hängt vom Ausgang des Zufallsexperiments ab.
Gewinnspiel: Wir spielen ein Spiel. Dabei ziehen wir einmal aus 32 Karten. Je nach Karte gibt es verschiedene Auszahlungen:
Herz Ass: Wir bekommen 20 Euro
Herz 10: Wir bekommen 10 Euro
Jede andere Karte: Wir zahlen 1 Euro
Die Variable \(X\) beschreibt den Gewinn nach einmaligem Ziehen. Daher kann \(X\) die Werte
\[\{-1, 10 , 20\}\]annehmen. Welchen konkreten Wert \(X\) annimmt, hängt vom Ausgang des Zufallsexperiments ab.
Wartezeit: Wir stehen mit einer Stoppuhr an der Kasse eines Supermarkts. Die Variable \(X\) beschreibt die Zeit (in Sekunden) die es dauert bis sich ein neuer Kunde an der Kasse anstellt. Daher kann \(X\) die Werte
\[ [0, \infty)\qquad \text{alle nicht-negativen reellen Zahlen}\]annehmen. Welchen konkreten Wert \(X\) annimmt, hängt vom Ausgang des Zufallsexperiments ab.
Die wesentlichen Aspekte dieser Beispiele fasst die folgende Defintion zum Begriff Zufallsvariable zusammen:
Definition
Eine Zufallsvariable ist eine Größe \(X\), welche
reelle Werte annehmen kann und
deren konkreter Wert vom Ausgang eines Zufallsexperiments abhängt.
Noch eine kleine Ergänzung für alle die es ganz genau wissen wollen:
Hinter dem Tellerrand …
Tatsächlich ist die Definition einer Zufallsvariable etwas aufwendiger: Man benötigt eine Ergebnismenge \(\Omega\) ein Wahrscheinlichkeitsmaß \(\mathbb P\) und die zuvor erwähnte Ereignisalgebra \(\mathcal A\). Ein Zufallsvariable \(X\) ist dann eine Abbildung \(X\) von \(\Omega\) nach \(\mathbb R\), so dass für jedes \(x\in \mathbb R\) gilt: \(\{\omega \in \Omega \mid X(\omega) \leq x\}\in \mathcal A\).
Wie bereits erwähnt, besteht \(\mathcal A\) aus den Mengen, welchen man eine Wahrscheinlichkeit zuordnen kann. Diese Definition sorgt dafür, dass alle Ereignisse die uns im Rahmen der Zufallsvariablen interessieren könnten dazu gehören - also mit einer Wahrscheinlichkeit bewertet werden können.
Arten von Zufallsvariablen#
Bei den einführenden Beispielen fällt folgendes auf:
die Beispiele Dreimaliger Münzwurf, Zwei Würfel und Gewinnspiel werden mit Zufallsvariablen beschrieben, die nur endliche viele Werte annehmen können
im Beispiel Wartezeit kann die Zufallsvariable eine beliebige Zahl größer gleich Null sein (z.B. sind gebrochene Zahlen möglich)
Dieser Unterschied zu den Begriffen diskrete und stetige Zufallsvariablen (siehe auch diskrete und stetige Merkmale in der deskriptiven Statistik). Wir wollen uns zunächst nur mit den diskreten Zufallsvariablen beschäftigen, daher halten wir die Definition hier fest:
Definition
Kann eine Zufallsvariable \(X\) nur endliche viele oder abzählbar unendlich viele Werte annehmen, so heißt sie diskrete Zufallsvariable. Die Menge der Werte die \(X\) annehmen kann, nennt man Träger oder Trägermenge von \(X\).
Der Begriff abzählbar unendlich bedeutet, dass die Möglichen Ausprägungen von \(X\) durchaus unendlich viele sein können, allerdings muss es möglich sein, sie systematisch mit den Zahlen \(1,2,3,\dots\) durchzunummerieren (also abzuzählen). Beispielsweise gibt es abzählbar unendlich viele Primzahlen, da es unendlich viele gibt und man sie der Größe nach durchnummerieren kann (1. die kleinste, 2. die zweitkleinste, 3. die drittkleinste, usw). Uns werden abzählbar unendliche Wertebereich zum Beispiel begegnen, wenn die Zufallsvarible Anzahlen angibt, zu denen es keine sinnvolle oberere Schranke gibt, z.B. Anzahl der eingehenden Anrufe in einer Servicezentrale innerhalb eines Tages.
Wahrscheinlichkeiten bei diskreten Zufallsvariablen#
Um Vorgänge mit Zufallsvariablen zu beschreiben, müssen wir noch klären, wie wahrscheinlich die möglichen Werte der Zufallsvariablen sind. Dazu kann man beispielsweise Wertetabellen nutzen, in denen man die Wahrscheinlichkeiten \(\mathbb P(X=x)\), dass \(X\) den Wert \(x\) annimmt, abträgt:
Wert \(x\) |
\(0\) |
\(1\) |
\(2\) |
\(3\) |
|---|---|---|---|---|
Wahrscheinlichkeit \(\mathbb P(X=x)\) |
\(0.125\) |
\(0.375\) |
\(0.375\) |
\(0.125\) |
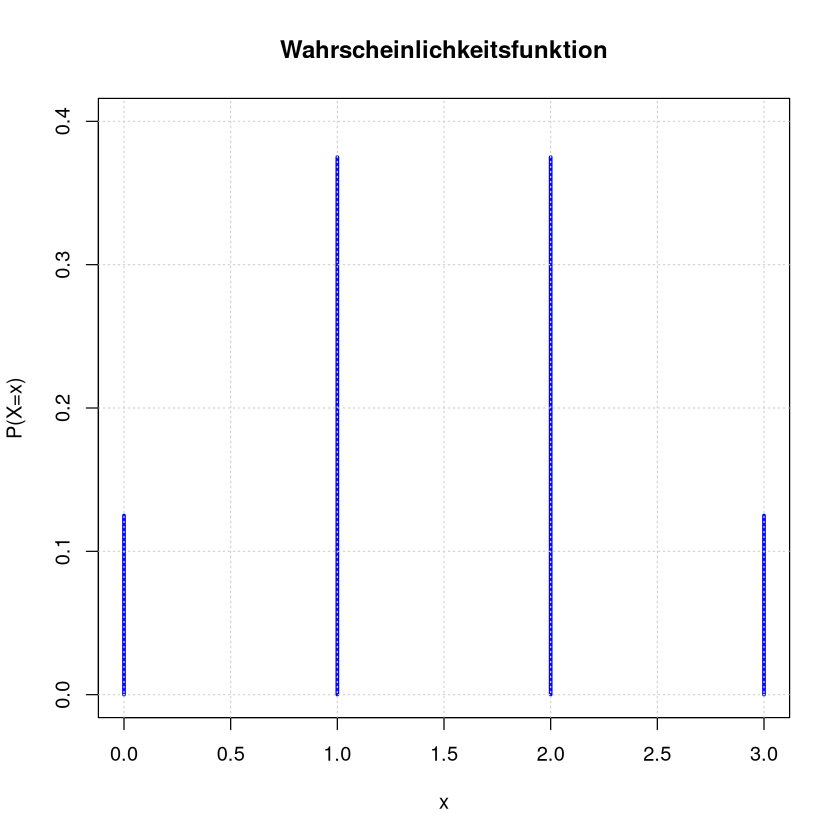
Hier sind beispielsweise die Wahrscheinlichkeiten zum Beispiel Dreimaliger Münzwurf dargestellt. Die Trägermenge ist hier \(T=\{0,1,2,3\}\).
Man kann dies auch mit der Wahrscheinlichkeitsfunktion beschreiben. Diese ist folgendermaßen definiert:
Definition
Ist \(X\) eine Zufallsvariable mit Träger \(T=\{x_1,x_2,\dots\}\), Dann ist die Wahrscheinlichkeitsfunktion \(f\) definiert durch
Dies stellt man graphisch in einem Stabdiagramm dar:
Show code cell source
x <- c(0,1,2,3)
probs <- c(0.125,0.375,0.375,0.125)
plot(x = x, y = probs, col = "blue", type = "h", lwd = 3,ylim=c(0,0.4),
main = "Wahrscheinlichkeitsfunktion", ylab = "P(X=x)", xlab = "x")
grid()
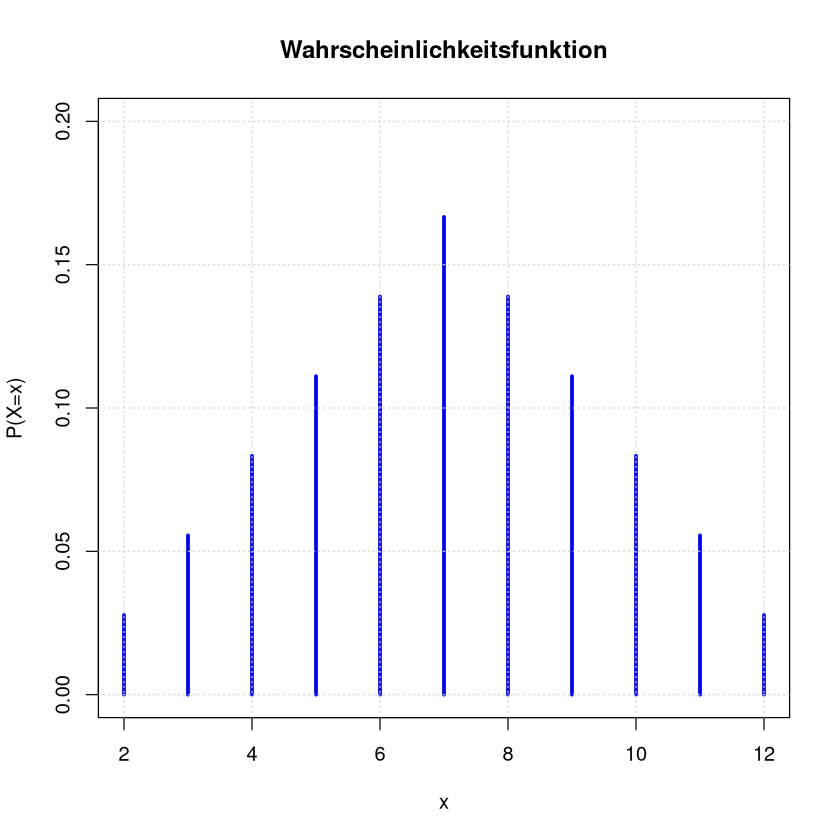
Für das Beispiel Zwei Würfel (Summe der beiden Würfel) sehen Wertetabelle und Stabdiagramm wie folgt aus:
Wert \(x\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
\(7\) |
\(8\) |
\(9\) |
\(10\) |
\(11\) |
\(12\) |
|---|---|---|---|---|---|---|---|---|---|---|---|
Wahrscheinlichkeit \(\mathbb P(X=x)\) |
\(\frac{1}{36}\) |
\(\frac{2}{36}\) |
\(\frac{3}{36}\) |
\(\frac{4}{36}\) |
\(\frac{5}{36}\) |
\(\frac{6}{36}\) |
\(\frac{5}{36}\) |
\(\frac{4}{36}\) |
\(\frac{3}{36}\) |
\(\frac{2}{36}\) |
\(\frac{1}{36}\) |
Show code cell source
x <- 2:12
probs <- c(1,2,3,4,5,6,5,4,3,2,1)/36
plot(x = x, y = probs, col = "blue", type = "h", lwd = 3,ylim=c(0,0.2),
main = "Wahrscheinlichkeitsfunktion", ylab = "P(X=x)", xlab = "x")
grid()
Mit den Zufallsvariablen lassen sich nun ganz verschiedene Ereignisse beschreiben, z.B. falls \(X\) die Augensumme beim zweimaligen Würfeln ist:
mit Zufallsvariable |
in Worten |
|---|---|
\(X>9\) |
Die Augensumme ist größer als \(9\) |
\(X\neq 8\) |
Die Augensumme ist keine \(8\) |
\(X\in\{ 2,4,6,8,10,12\}\) |
Die Augensumme ist gerade |
\(X\leq 9\) |
Die Augensumme ist maximal \(9\) |
Um Wahrscheinlichkeiten dieser Ereignisse zu berechnen müssen nur die Wahrscheinlichkeiten zu den zugehörigen \(x\)-Werten addiert werden:
\(\mathbb P(X>9)= \mathbb P(X=10)+\mathbb P(X=11)+\mathbb P(X=12)=\frac{3}{36}+\frac{2}{36}+\frac{1}{36}=\frac16\)
\(\mathbb P(X\neq 8)= 1-\mathbb P(X=8) = 1-\frac{5}{36} = \frac{31}{36}\)
\(\mathbb P(X\in\{ 2,4,6,8,10,12\})=\mathbb P(X=2)+\mathbb P(X=4)+\mathbb P(X=6)+\mathbb P(X=8)+\mathbb P(X=10)+\mathbb P(X=12)\) \(=\frac{1}{36}+\frac{3}{36}+\frac{5}{36}+\frac{5}{36}+\frac{3}{36}+\frac{1}{36}=\frac12\)
\(\mathbb P(X\leq 9 )= 1- \mathbb P(X > 9)=1-\frac16=\frac56\)
Halten wir das noch als allgemeine Rechenregeln fest
Rechenregeln
Ist \(X\) ein diskrete Zufallsvariable mit Trägermenge \(T=\{x_1,x_2,\dots\}\), so gilt
\(\displaystyle \mathbb P(X\in A) = \sum_{i: x_i\in A} \mathbb P(X=x_i)\)
\(\displaystyle \mathbb P(X\leq t) = \sum_{i: x_i \leq t} \mathbb P(X=x_i)\)
\(\displaystyle \mathbb P(s\leq X\leq t) = \sum_{i: s\leq x_i \leq t} \mathbb P(X=x_i)\)
usw.
Verteilungsfunktion#
Kennt man alle Wahrscheinlichkeiten vom Typ \(\mathbb P(X\leq t)\) für \(t\in\mathbb R\), so lässt sich jede andere Wahrscheinlichkeit daraus berechnen. Daher hat die folgende Funktion eine besondere Bedeutung für die Zufallsvariablen:
Definition
Ist \(X\) eine Zufallsvariable, so heißt die Funktion
Verteilungsfunktion von \(X\).
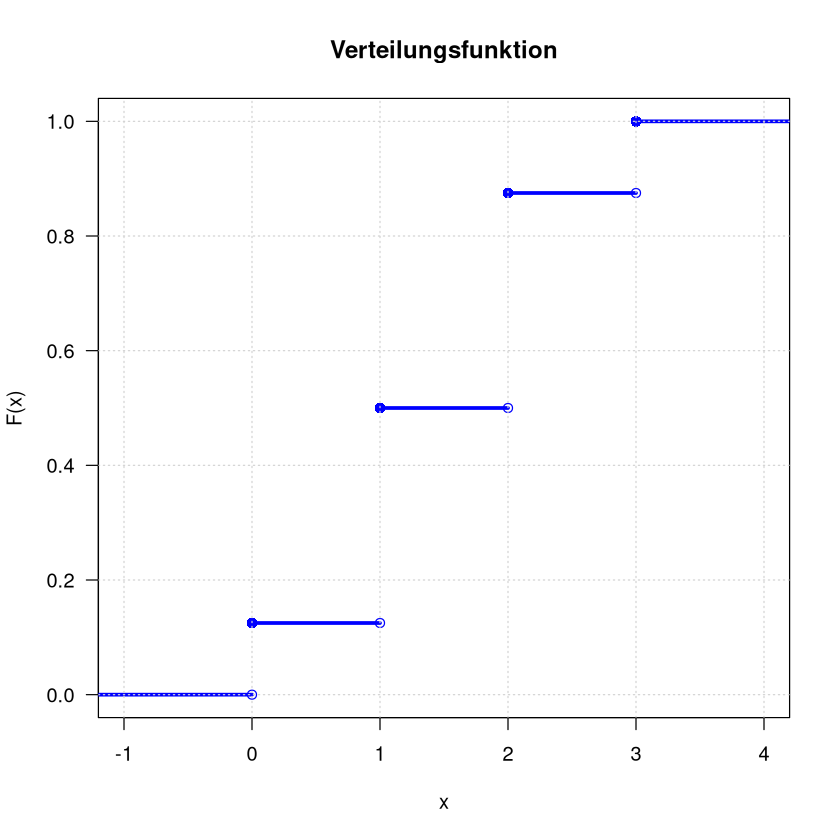
Die Verteilungsfunktion zum Beispiel Drei Münzen ist
und in der Grafik sieht die so aus:
Show code cell source
plot.dcdf <- function(x, prob , col="blue", lwd=3, ...) {
y <- c(0,cumsum(prob))
cdf <- stepfun(x=x, y=y, right=TRUE)
plot(cdf, verticals=FALSE,
lwd=lwd, col=col, las=1,
xlab="x", ylab="F(x)", ...)
points(x,cumsum(prob),pch = 16, col=col, cex=1.2)
}
plot.dcdf(c(0,1,2,3), c(1,3,3,1)/8, main="Verteilungsfunktion")
grid()
Eigenschaften der Verteilungsfunktion
Ist \(F\) die Verteilungsfunktion der Zufallsvariable \(X\), so gilt
Die Funktionswerte liegen immer zwischen \(0\) und \(1\), d.h. \(0\leq F(x) \leq 1\) für alle \(x\)
\(F\) ist monoton wachsend, d.h. gilt \(a\leq b\), so gilt \(F(a)\leq F(b)\)
„Sprunghöhe von \(F\) bei \(a\)“ \(=\) \(\mathbb P(X=a)\)
Der Funktionswert an einer Sprungstelle \(a\) ist immer „oben“, d.h. die Funktion ist rechtsstetig.
Beachte: Die Definition der Verteilungsfunktion und die aufgeführten Eigenschaften der Verteilungsfunktion gelten so für beliebige Zufallsvariablen (nicht nur für diskrete).
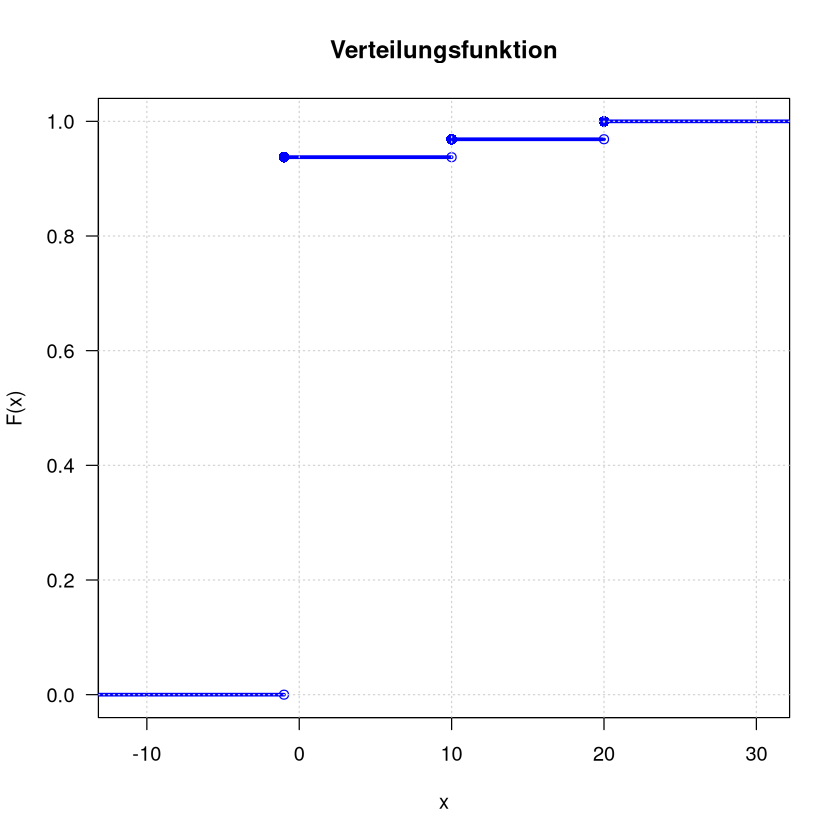
Gewinnspiel-Beispiel#
Schauen wir uns zum Abschluss noch einmal das Gewinnspiel-Beispiel etwas genauer an. Die Regeln waren wie folgt: Wir ziehen einmal aus 32 Karten. Je nach Karte gibt es verschiedene Auszahlungen:
Herz Ass: Wir bekommen 20 Euro
Herz 10: Wir bekommen 10 Euro
Jede andere Karte: Wir zahlen 1 Euro
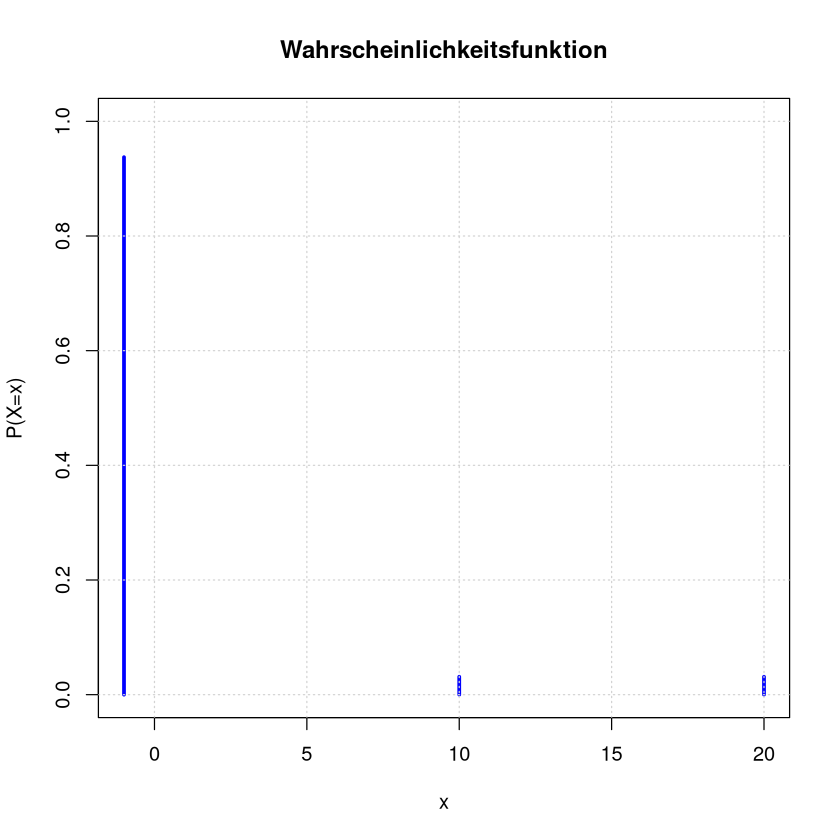
Die Zufallsvariable \(X\) beschreibt den Gewinn nach einmaligem Ziehen. Sie wird also durch die folgenden Wertetabelle beschrieben:
Wert \(x\) |
-1 |
10 |
20 |
|---|---|---|---|
\(\mathbb P (X=x)\) |
\(\frac{30}{32}\) |
\(\frac{1}{32}\) |
\(\frac{1}{32}\) |
Im Stabdiagramm dargestellt, sieht das wie folgt aus:
Show code cell source
x <- c(-1,10,20)
probs <- c(30,1,1)/32
plot(x = x, y = probs, col = "blue", type = "h", lwd = 3,ylim=c(0,1),
main = "Wahrscheinlichkeitsfunktion", ylab = "P(X=x)", xlab = "x")
grid()
und die zugehörige Verteilungsfunktion ist