Nominales und metrisches Merkmal

Nominales und metrisches Merkmal#

Hier betachten wir den Fall, dass eine bivariate Stichprobe mit einem nominalen und einem metrischen Merkmal erhoben wird. Wir betachten hier also eine Stichprobe

\[ (x_1,y_1), (x_2,y_2), \dots, (x_n, y_n) \]

zum nominalen Merkaml \(X\) und zum metrischen Merkmal \(Y\).

Maßzahlen#

Wird ein nominales und ein metrisches Merkmal in einer bivariaten Stichprobe erhoben, so geht man typischweise wie folgt vor:

  • Einteilung des metrischen Merkmals in Gruppen, entsprechend des nominalen Merkmal

  • Berechnung der bekannten Maßzahlen für univariate metrische Stichproben pro Gruppe, siehe Maßzahlen für univariate Stichproben.

  • Gegenüberstellung der Maßzahlen in einer Tabelle oder in graphischen Darstellungen, siehe unten.

Umsetzung in R#

Wir betrachten hier gern den iris-Datensatz als Beispiel. Dieser ist in R schon enthalten. Er enthält Messungen von drei verschiedenen Blumenarten (Species) der Gattung Iris:

Sepal.Length

Sepal.Width

Petal.Length

Petal.Width

Species

5.1

3.5

1.4

0.2

setosa

4.9

3.0

1.4

0.2

setosa

…

…

…

…

…

6.3

3.3

6.0

2.5

virginica

Insgesamt gibt es:

  • 150 Beobachtungen

  • 3 Arten: setosa, versicolor, virginica

  • 4 Messgrößen (Längen und Breiten von Blütenblättern und Kelchblättern)

Wir stellen uns vor es liegt nur eine der Messgröße (z.B. nur die erste Spalte) und die letzte Spalte vor.

Im ersten Schritt lernen wir, wie man mit dem Befehl aggregate() kennen. Damit kann man eine Funktion auf die Elemente einer Untergruppe anwenden. Dabei bedeutet Sepal.Length ~ Species, dass wir die Größe Sepal.Length entsprechend der Speziesin Gurppen aufteilen und pro Gruppe die Funktion anwenden wollen. Genauer wird das unten erklärt.

# Mittelwerte berechnen
mittel <- aggregate(Sepal.Length ~ Species, iris, mean)
# Standardabweichung berechnen
abweichung <- aggregate(Sepal.Length ~ Species, iris, sd)

# Zusammenführen
data_iris <- data.frame(
  name = mittel[,1],
  mean = mittel[,2],
  sd = abweichung[,2]
)

data_iris
A data.frame: 3 × 3
namemeansd
<fct><dbl><dbl>
setosa 5.0060.3524897
versicolor5.9360.5161711
virginica 6.5880.6358796

Erläuterung des Codes

  • mittel <- aggregate(Sepal.Length ~ Species, iris, mean)

    Was passiert hier?

    • aggregate() ist eine Funktion, mit der man Berechnungen für Gruppen in einem Dataframe durchführen kann.

    • Sepal.Length ~ Species bedeutet: Berechne etwas für die Spalte Sepal.Length, gruppiert nach der Spalte Species.

    • iris ist der Datensatz.

    • mean gibt an, dass der Mittelwert (Durchschnitt) berechnet wird.

  • abweichung <- aggregate(Sepal.Length ~ Species, iris, sd)

    Die Funktion ist genau gleich wie oben, aber diesmal wird sd (Standardabweichung) berechnet.

  • ergebnis <- data.frame( name = mittel[,1], mean = mittel[,2], sd = abweichung[,2])

    Was passiert hier?

    • mittel[,1]: Die erste Spalte von mittel enthält die Artennamen (Species).

    • mittel[,2]: Die zweite Spalte enthält die Mittelwerte.

    • abweichung[,2]: Die zweite Spalte von abweichung enthält die Standardabweichungen.

Graphische Darstellungen#

Boxplots#

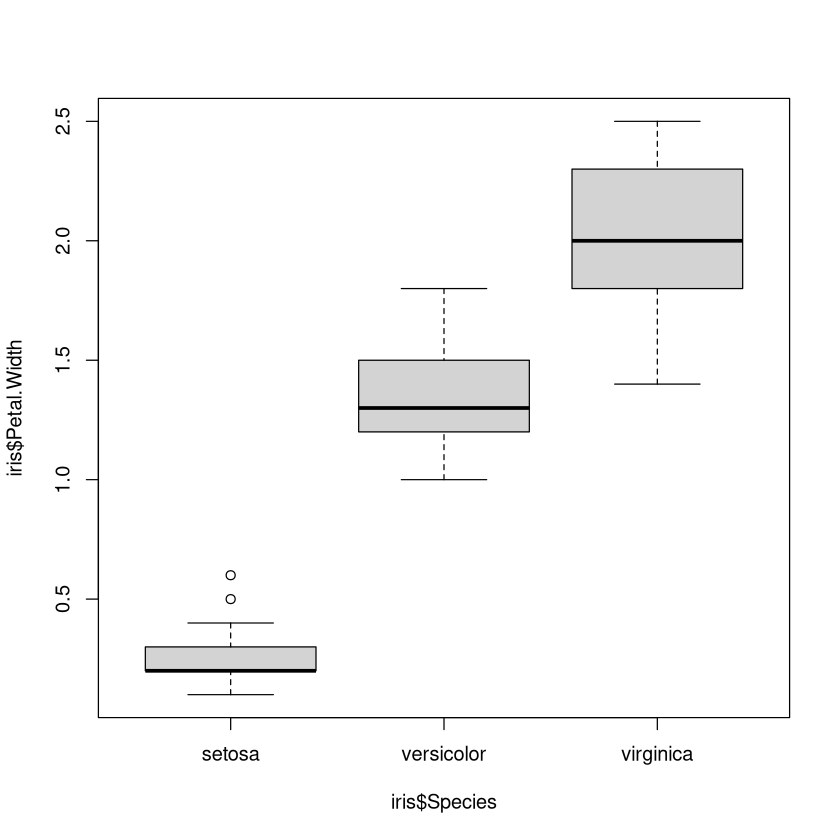
Wir haben Boxplots bereits kennengelernt. In der vorliegenden Situation kann für jede Ausprägung des nominalen Merkmals ein separater Boxplot des metrischen Merkmals dargestellt werden. Dadurch lassen sich zentrale Tendenzen (Median) und die Streuung innerhalb der Gruppen vergleichen. Zudem können potenzielle Ausreißer sichtbar gemacht werden. Boxplots sind besonders nützlich, um Unterschiede in der Verteilung zwischen den Gruppen zu analysieren.

Die Umsetzung in R haben wir bereits im Kapitel Mehrere Boxplots in einer Grafik kennengelernt. Der Befehl lautet boxplot(iris$Petal.Width ~ iris$Species), wobei der Ausdruck iris$Petal.Width ~ iris$Species im Sinne von R ein „Formel“ ist. Sie sagt, wir möchten die Variable iris$Petal.Width mit Hilfe der Variablen iris$Species beschreiben.

boxplot(iris$Petal.Width ~ iris$Species)
../../_images/b19be1b4e85657d43513ea207c339f7f4afbf5e8cd60dd01e4383976e533c6df.png

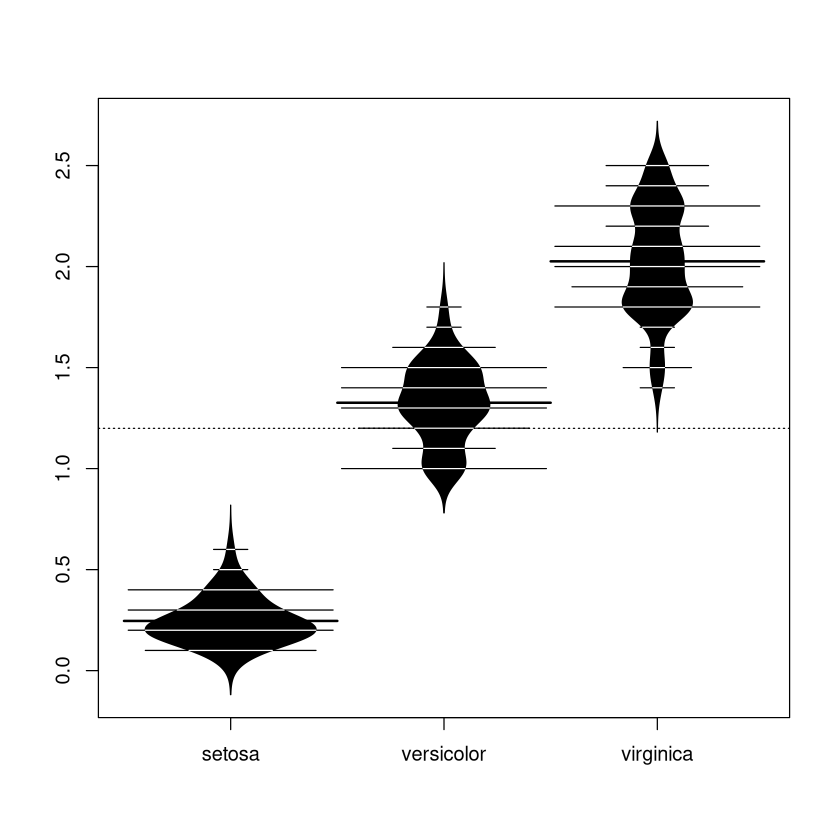
Bean-Plots#

An dieser Stelle möchten wir auch die sogenannten Bean-Plots erwähnen. Sie sind in R darstellbar unter Verwendung des Pakets beanplot. Die Verwendung ist ähnlich wie beim Boxplot. Man kann einen Datensatz oder wie hier im Beispiel 3 Datensätze, eingeteilt nach der Variablen iris$Species, darstellen. Dort wo der Bean-Plot am breitesten ist, sind besonders viele Daten gemessen worden, dort wo er schmal ist sehr wenige. Man kann sich den Bean-Plot vorstellen als auf die Seite gelegtes Histogramm, welches durch eine stetige Funktion approximiert und anschließend gespiegelt wurde.

Auf mehr Details zum Bean-Plot wollen wir an dieser Stelle verzichten.

library(beanplot)
beanplot(iris$Petal.Width~iris$Species)
../../_images/0d25639cfaeb7b518f107164d90c94fd2b282932a5d7c520b886a45588af75af.png

Säulendiagramme mit Fehlerbalken#

Wie oben, teilen wir die metrischen Daten entsprechend der nominalen Daten in Gruppen auf. Wir berechnen für jede Gruppe den Mittelwert und die Standardabweichung. Dargestellt wir nun pro Gruppe ein Säule, deren Höhe das arithmetische Mittel ist. Zusätzlich wird dann um das obere Ende der Säule ein Intervall veranschaulicht. Diese Intervalle nennt man Fehlerbalken. Sie sehen den Whiskers beim Boxplot ähnlich. Vom oberene Ende der Säule geht man \(a\) noch oben und \(a\) nach unten, so dass die Länge genau \(2\cdot a\) ist. Für spezielle Wahl von \(a\) gibt es verschiedene Ansätze, z.B. \(a=s\) (Standardabweichung) oder \(a=s/\sqrt{n}\) (Standardfehler). Daher ist es wichtig in der Erläuterung zu Grafik die Fehlerbalken zu erklären.

Umsetzung in R mit ggplot2#

Wir verwenden hier das Paket ggplot2. Dies bietet sehr umfangreiche Möglichkeiten Grafiken zu erstellen. Allerdings ist die Syntax etwas anders als gewohnt. Daher soll hier der Code noch einmal ausführlich erklärt werden.

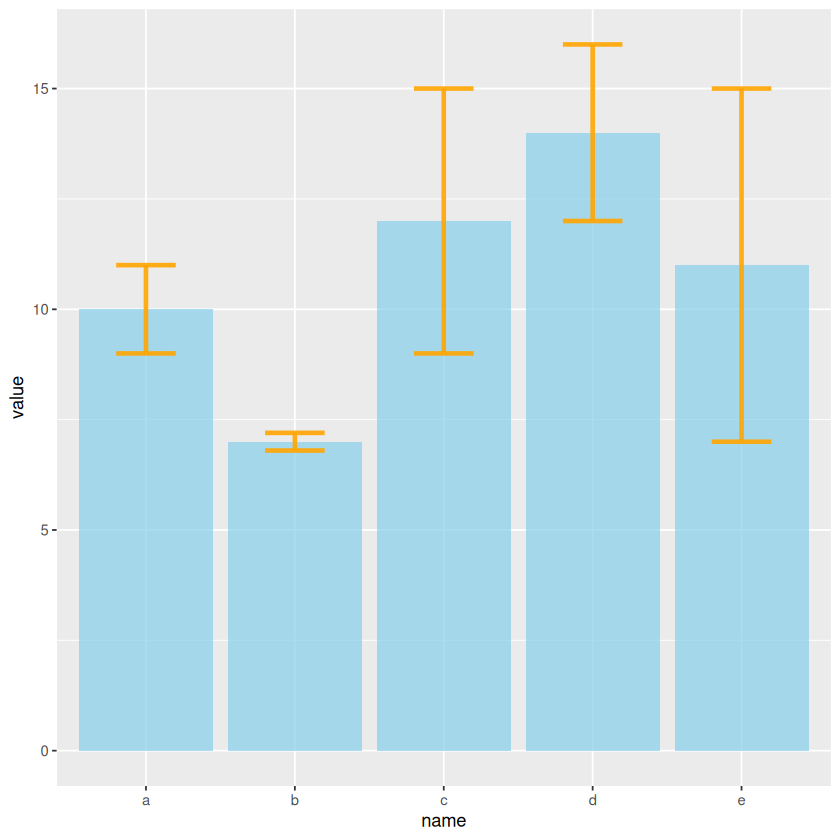
library("ggplot2")

data <- data.frame(
  name=letters[1:5],
  value=sample(seq(4,15),5),
  sd=c(1,0.2,3,2,4)
)
 
# Most basic error bar
ggplot(data) +
    geom_bar( aes(x=name, y=value), stat="identity", fill="skyblue", alpha=0.7) +
    geom_errorbar( aes(x=name, ymin=value-sd, ymax=value+sd), width=0.4, colour="orange", alpha=0.9, linewidth=1.3)
../../_images/231423e2136865d08daad58ca566678e89474a65d8018ca11c41f7f109f2dcc4.png

Erläuterung des Codes

  • library("ggplot2") Mit diesem Befehl wird das Paket ggplot2 geladen. Das Paket gehört zu den wichtigsten Paketen für die Datenvisualisierung in R, weil es sehr flexibel und leistungsstark ist.

  • data <- data.frame(name=letters[1:5],value=sample(seq(4,15),5),sd=c(1,0.2,3,2,4)) Hier wird ein Dataframe erstellt, also eine Tabelle mit drei Spalten:

    name

    value

    sd

    a

    5

    1

    b

    8

    0.2

    c

    12

    3

    d

    10

    2

    e

    6

    4

    Was bedeuten die Spalten?

    • name: Die Namen der Balken (a bis e)

    • value: Die Höhe der Balken (zufällig gewählt zwischen 4 und 15)

    • sd: Die Standardabweichung, also wie stark die Werte schwanken können. Sie wird für die Fehlerbalken genutzt.

  • ggplot(data) + geom_bar(aes(x=name, y=value), stat="identity",fill="skyblue", alpha=0.7) Das passiert hier Schritt für Schritt:

    • ggplot(data) erstellt das Grundgerüst für den Plot mit den Daten aus dem data-Dataframe.

    • geom_bar() zeichnet Balken.

    • Das Argument aes(x=name, y=value) sagt aus, dass die Namen auf der \(x\)-Achse stehen und die Werte auf der \(y\)-Achse.

    • stat="identity" bedeutet, dass die Balken direkt die angegebenen Werte (value) anzeigen sollen. Standardmäßig zählt ggplot2 sonst einfach die Anzahl der Werte (wie ein Histogramm).

    • ‚fill=“skyblue“‘ gibt die Farbe der Balken an.

    • alpha=0.7 macht die Balken etwas durchsichtig (70% Deckkraft).

  • geom_errorbar(aes(x=name, ymin=value-sd, ymax=value+sd), width=0.4, colour="orange", alpha=0.9, linewidth=1.3) Mit ‚geom_errorbar()‘ werden Fehlerbalken (Error Bars) gezeichnet.

    • aes(): Hier wird angegeben, wo die Fehlerbalken gezeichnet werden.

    • x=name: Die Fehlerbalken stehen bei den gleichen Kategorien wie die Balken.

    • ymin=value-sd: Der untere Punkt des Balkens (Wert minus Standardabweichung).

    • ymax=value+sd: Der obere Punkt des Balkens (Wert plus Standardabweichung).

    Die zusätzlichen Einstellungen:

    • width=0.4: Die Breite der horizontalen Linie am oberen und unteren Ende.

    • colour="orange": Die Farbe der Fehlerbalken.

    • alpha=0.9: Transparenz (90% Deckkraft).

    • linewidth=1.3: Die Linienstärke der Fehlerbalken.

Merke:

  • In ggplot2 werden Diagramme Schicht für Schicht (Layer) aufgebaut.

  • Schichten werden mit + getrennt.

  • Jede Schicht fügt neue Elemente hinzu.

  • Die Funktion aes() (Ästhetik) gibt an, welche Daten auf die Achsen kommen.

Nun wollen wir die Daten aus dem Datensatz iris für die Darstellung mit den Fehlerbalken vorbereiten. Dazu gehen wir wie oben vor und nutzen die Funktion aggregate().

# Mittelwerte berechnen
mittel <- aggregate(Sepal.Length ~ Species, iris, mean)
# Standardabweichung berechnen
abweichung <- aggregate(Sepal.Length ~ Species, iris, sd)

# Zusammenführen
data_iris <- data.frame(
  name = mittel[,1],
  mean = mittel[,2],
  sd = abweichung[,2]
)

data_iris
A data.frame: 3 × 3
namemeansd
<fct><dbl><dbl>
setosa 5.0060.3524897
versicolor5.9360.5161711
virginica 6.5880.6358796

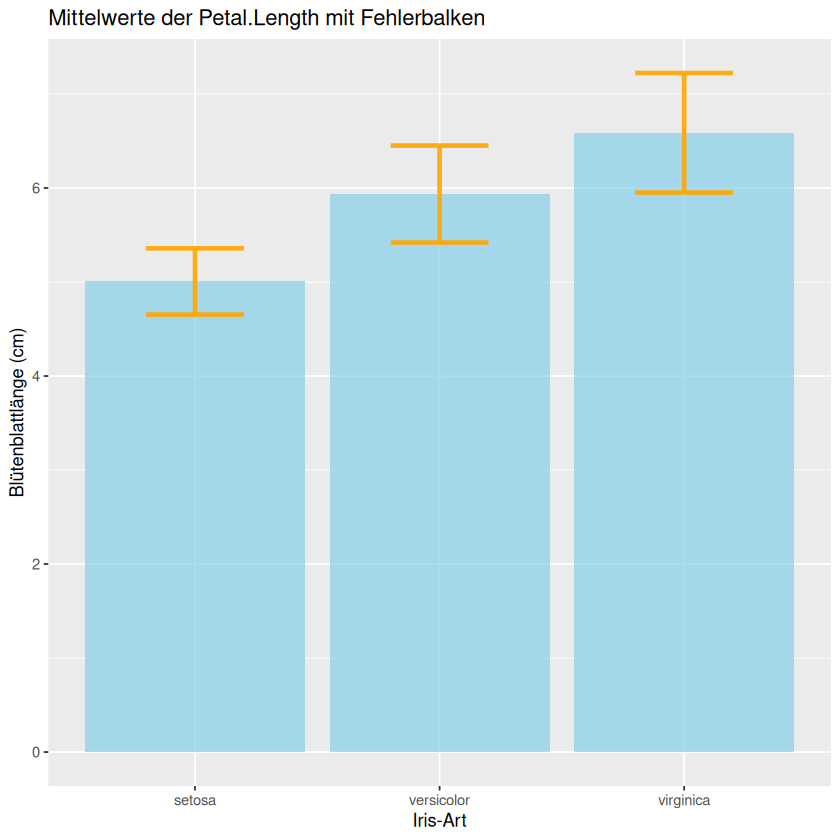
Nun schauen wir uns das Säulendiagramm mit den Fehlerbalken für die erste Spalte der iris Daten an.

library("ggplot2")
 
# Most basic error bar
ggplot(data_iris) +
    geom_bar( aes(x=name, y=mean), stat="identity", fill="skyblue", alpha=0.7) +
    geom_errorbar( aes(x=name, ymin=mean-sd, ymax=mean+sd), width=0.4, colour="orange", alpha=0.9, linewidth=1.3) + 
    labs(title = "Mittelwerte der Petal.Length mit Fehlerbalken",
       x = "Iris-Art",
       y = "Blütenblattlänge (cm)")
../../_images/e5423e808b685c8034587a3e262eb73712d823b6a000dacee9938601d483e1e2.png

Mit dem Befehl

labs(title = "Mittelwerte der Petal.Length mit Fehlerbalken",        x = "Iris-Art", y = "Blütenblattlänge (cm)")

haben wir noch die Achsenbeschriftung und den Titel angepasst.